Special Topics in Data Engineering Panagiotis Karras CS

Special Topics in Data Engineering Panagiotis Karras CS 6234 Lecture, March 4 th, 2009

Outline • Summarizing Data Streams. • Efficient Array Partitioning. 1 D Case. 2 D Case. • Hierarchical Synopses with Optimal Error Guarantees.

Summarizing Data Streams • Approximate a sequence [d 1, d 2, …, dn] with B buckets, si = [bi, ei, vi] so that an error metric is minimized. • Data arrive as a stream: Seen only once. Cannot be stored. • Objective functions: Max. abs. error: Euclidean error:

Histograms [KSM 2007] • Solve the error-bounded problem. Maximum Absolute Error bound ε = 2 4 5 6 2 15 17 3 6 9 12 … [ 4 ] [ 16 ] [ 4. 5 ] [… • Generalized to any weighted maximum-error metric. Each value di defines a tolerance interval Bucket closed when running intersection of interval becomes null Complexity:

Histograms • Apply to the space-bounded problem. Perform binary search in the domain of the error bound ε For error values requiring space , with actual error Error-bounded algorithm running under constraint If requires , run an optimality test: instead of space, then optimal solution has been reached. Complexity: Independent of buckets B What about streaming case?

Streamstrapping [Guha 2009] • Metric error satisfies property: • Run multiple algorithms. 1. Read first B items, keep reading until first error (>1/M) 2. Start versions for 3. When a version for some fails, a) Terminate all versions for b) Start new versions for using summary of 4. Repeat until end of input. as first input.

Streamstrapping [Guha 2009] • Theorem: For any running • Proof: Stream. Strap algorithm achieves an approximation, copies and initializations. Consider lowest value of for which an algorithm runs. Suppose error estimate was raised j times before reaching Xi : prefix of input just before error estimate was raised for i th time. Yj : suffix between (j-1)th and jth raising of error estimate. Hi : summary built for Xi. Then: target error added error Furthermore: recursion Error estimate is raised by at every time.

Streamstrapping [Guha 2009] • Proof (cont’d): Putting it all together, telescoping: added error Total error is: optimal error Moreover, However, Thus, In conclusion, total error is # Initializations follows. (algorithm failed for it)

Streamstrapping [Guha 2009] • Theorem: Algorithm runs in space and time. • Proof: Space bound follows from copies. Batch input values in groups of Define binary tree of t values, compute min & max over tree nodes: Using tree, max & min of any interval computed in Every copy has to check violation of its bound over t items. Non-violation decided in O(1). Total Violation located in. For all buckets, Over all algorithms it becomes:

1 D Array Partitioning [KMS 1997] • Problem: Partition an array of n items into p intervals so that the maximum weight of the intervals is minimized. Arises in load balancing in pipelined, parallel environments.

1 D Array Partitioning [KMS 1997] • Idea: Perform binary search on all possible O(n 2) intervals responsible for maximum weight result (bottlenecks). • Obstacle: Approximate median has to be calculated in O(n) time.

1 D Array Partitioning [KMS 1997] • Solution: Exploit internal structure of O(n 2) intervals. n columns, column c consisting of Monotonically non-increasing

1 D Array Partitioning [KMS 1997] • Calls to F(. . . ) need O(1). (why? ) • Median of any subcolumn determined with one call to F oracle. (how? ) Splitter-finding Algorithm: • Find median weight in each active subcolumn. • Find median of medians m in O(n) (standard). • Cl (Cr): set of columns with median < (>) m.

1 D Array Partitioning [KMS 1997] • The median of medians m is not always a splitter.

1 D Array Partitioning [KMS 1997] • If median of medians m is not a splitter, recur to set of active subcolumns (Cl or Cr) with more elements (ignored elements still considered in future set size calculations). • Otherwise, return m as a good splitter (approximate median). End of Splitter-finding Algorithm.

1 D Array Partitioning [KMS 1997] 1. 2. 3. 4. 5. Overall Algorithm: Arrange intervals in subcolumns. Find a splitter weight m of active subcolumns. Check whether array is partitionable in p intervals of maximum weight m (how? ) If true, then m is upper bound of optimal maximum weight, eliminate half of elements of each subcolumn in Cl - otherwise in Cr. Recur until convergence to optimal m. Complexity: O(n log n)

2 D Array Partitioning [KMS 1997] • Problem: Partition a 2 D array of n x n items into a p x p partition (inducing p 2 blocks) so that the maximum weight of the blocks is minimized. Arises in particle-in-cell computations, sparse matric computations, etc. • NP-hard [GM 1996] • APX-hard [CCM 1996]

2 D Array Partitioning [KMS 1997] • Definition: Two axis-parallel rectangles are independent if their projections are disjoint along both the x-axis and the y-axis. • Observation 1: If an array has a partition, then it may contain at most independent rectangles of weight strictly greater than W. (why? )

2 D Array Partitioning [KMS 1997] • At least one line needed to stab each of the independent rectangles. • Best case: independent rectangles

2 D Array Partitioning [KMS 1997] The Algorithm: Assume we know optimal W. Step 1: (define P ) Given W, obtain partition such that each row/column within any block has weight at most 2 W. (how? ) Independent horizontal/vertical scans, keeping track of running sum of weights of each row/column in block. (why exists ? )

2 D Array Partitioning [KMS 1997] Step 2: (from P to S ) Construct set of all minimal rectangles of weight more than W, entirely contained in blocks of. (how? ) Start from each location within block, consider all possible rectangles in order of increasing sides, until W exceeded, keep minimal ones. Property of S : block weight at most 3 W. (why? ) Hint : rows/columns in blocks of P at most 2 W.

2 D Array Partitioning [KMS 1997] Step 3: (from S to M ) Determine local 3 -optimal set independent rectangles. of 3 -optimality : There does not exist set of independent rectangles in that, added to after removing rectangles from it, do not violate independence condition. Polynomial-time construction (how? with swaps: local optimality easy)

2 D Array Partitioning [KMS 1997] Step 4: (from M to new partition) For each rectangle in M, set two straddling horizontal and two straddling vertical lines that induce it. At most partition derived New partition: P from step 1 together with this. horizontal lines vertical lines

2 D Array Partitioning [KMS 1997] Step 5: (final) Retain every th horizontal line, every th vertical line. Maximum weight increased at most by

2 D Array Partitioning [KMS 1997] Analysis: We have to show that: a. Given W (large enough) such that there exists partition, the maximum block weight in constructed partition is b. Minimum W for which analysis holds (found by binary search) is upper bound to optimum W.

2 D Array Partitioning [KMS 1997] Lemma 1: (at Step 1) Let block b contained in partition P. If b exceeds 27 W, then b can be partitioned in 3 independent rectangles of weight >W. Proof: Vertical scan in b, cut as soon as seen slab weight exceeds 7 W. (hence slab weight < 9 W ) (why? ) Horizontal scan, cut as soon as one seen slab weight exceeds W.

2 D Array Partitioning [KMS 1997] Proof (cont’d): Slab weight exceeding W does not exceed 3 W. (why? ) Eventually, 3 rectangles weighting >W each.

2 D Array Partitioning [KMS 1997] Lemma 2: (at Step 4) Weight of any block of Step-4 -partition is Proof: Case 1: Weight of b is O(W). (recall block in S <3 W ) Case 2: Weight of b is <27 W. If >27 W, then b partitionable in 3 independent rectangles, which can substitute the at most 2 blocks in M non-independent of b: violates 3 -optimality of M.

2 D Array Partitioning [KMS 1997] Lemma 3: (at Step 3) If , then Proof: Weight of rectangles in M is >W. By Observation 1, at most independent rectangles can be contained in M.

2 D Array Partitioning [KMS 1997] Lemma 4: (at Step 5) If , weight of any block in final solution is Proof: At Step 5, maximum weight increased at most by By Lemma 2, maximum weight is Hence, final weight is (a) Least W for which Step 1 and Step 3 succeed exceeds optimum W. Found by binary search. (b)

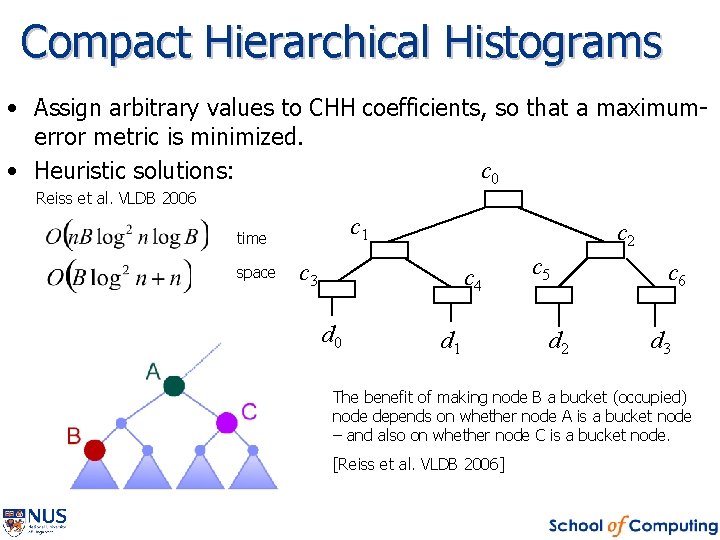
Compact Hierarchical Histograms • Assign arbitrary values to CHH coefficients, so that a maximumerror metric is minimized. c 0 • Heuristic solutions: Reiss et al. VLDB 2006 c 1 time space c 2 c 3 c 4 d 0 d 1 c 5 d 2 c 6 d 3 The benefit of making node B a bucket (occupied) node depends on whether node A is a bucket node – and also on whether node C is a bucket node. [Reiss et al. VLDB 2006]

Compact Hierarchical Histograms • Solve the error-bounded problem. Next-to-bottom level case c 2 i ci c 2 i+1 c 2 i ci

Compact Hierarchical Histograms • Solve the error-bounded problem. General, recursive case time Complexity: (space-efficient) space • Apply to the space-bounded problem. Complexity: Polynomially Tractable

References 1. P. Karras, D. Sacharidis, N. Mamoulis: Exploiting duality in summarization with deterministic guarantees. KDD 2007. 2. S. Guha: Tight results for clustering and summarizing data streams. ICDT 2009. 3. S. Khanna, S. Muthukrishnan, S. Skiena: Efficient Array Partitioning. ICALP 1997. 4. F. Reiss, M. Garofalakis, and J. M. Hellerstein: Compact histograms for hierarchical identifiers. VLDB 2006. 5. P. Karras, N. Mamoulis: Hierarchical synopses with optimal error guarantees. ACM TODS 33(3): 2008.

Thank you! Questions?