SL Gaps SL 1 Check SLpy ypoyp gaps

SL Gaps (SL) 1. Check SLp(y) ≡ (y-p)o(y-p) gaps (using a p grid). Dot Gaps - Sparse Ends (DG-SE) 1. Check Dotpq(y) ≡ (y-p)o(p-q)/|p-q| gaps (using grids for p and d=(p-q)/|p-q|? ). 1. 1 Check distances at sparse extremes. SPD Gaps (SPD) 1. Check SPDpq(y) ≡ SLp(y) - Dotpq(y)2 gaps Dot Gaps - KMeans (DG-KM) 1. Check Dotp, d(y) gaps (grids of p and d? ). 1. 1 Check distances at sparse extremes. 2. After several rounds of 1, apply k-means to the resulting clusters (when k seems to be determined). Dot Gaps - Density Analysis (DG-DA) 1. Check Dotp, d(y) gaps (grids of p and d? ) against density of subcluster. 1. 1 Check distances at sparse extremes against subcluster density. 2. Apply other methods once Dot ceases to be effective. Dot Gaps - Square Length (DG-SL) 1. Check Dotp, d(y) (over grid of p, d) and SLp(y) (over grid of p). 1. 1 Check sparse ends distance with subcluster density. (Dotpd , SLp share construction steps!) SL Gaps - Dot Gaps - Square Length Gaps (SL-DG-SPD) (Dotpq , SLp and SPDpq share construction steps! SLp(y) ≡ (y-p)o(y-p) = yoy - 2 yop +pop Dotpq(y) ≡ (y-p)od=yod-pod= (1/|p-q|)yop - (1/|p-q|)yoq Calc yoy, yop, yoq concurrently? Then constant multiplies 2*yop, (1/|p-q|)*yop concurrently. Then add | subtract. Calculate Dotpq(y)2. Then subtract it from SLp(y)

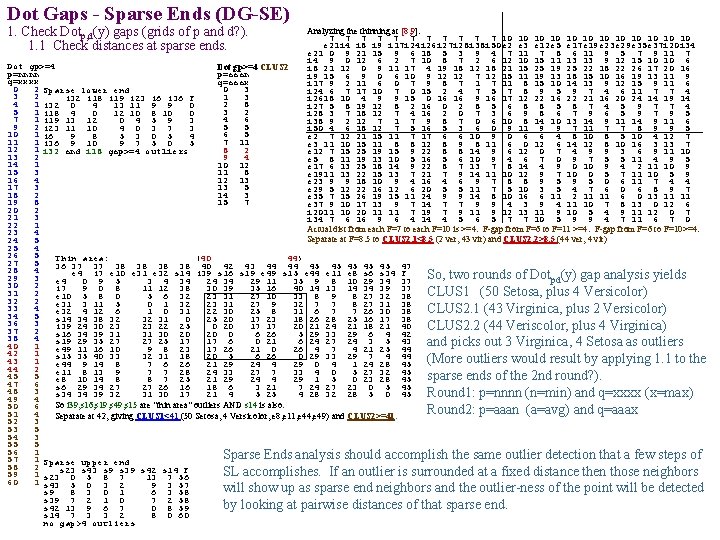
Dot Gaps - Sparse Ends (DG-SE) 1. Check Dotp, d(y) gaps (grids of p and d? ). 1. 1 Check distances at sparse ends. Analyzing the thinning at [8, 9]: 7 7 7 10 10 10 e 21 i 4 i 8 i 9 i 17 i 24 i 26 i 27 i 28 i 38 i 50 e 2 e 3 e 12 e 5 e 17 e 19 e 23 e 29 e 35 e 37 i 20 i 34 e 21 0 9 21 15 9 6 18 5 3 9 4 7 11 7 8 6 11 9 5 7 9 11 7 i 4 9 0 12 6 2 7 10 8 7 2 6 12 10 15 11 13 13 9 12 15 10 10 6 i 8 21 12 0 9 11 17 4 19 18 12 18 21 15 25 19 25 22 18 22 26 17 20 16 i 9 15 6 9 0 6 10 9 12 12 7 12 15 11 19 13 18 15 10 16 19 13 11 9 i 17 9 2 11 6 0 7 9 8 7 11 8 15 10 14 13 9 12 15 9 11 6 i 24 6 7 17 10 7 0 15 2 4 7 5 7 8 9 5 9 7 4 6 11 7 7 4 i 2618 10 4 9 9 15 0 16 16 9 16 17 12 22 16 22 21 16 20 24 14 19 14 i 27 5 8 19 12 8 2 16 0 2 8 5 6 8 8 5 8 7 4 5 9 7 7 4 i 28 3 7 18 12 7 4 16 2 0 7 3 6 9 8 6 7 9 6 5 9 7 9 5 i 38 9 2 12 7 1 7 9 8 7 0 6 10 8 14 10 13 14 9 11 6 i 50 4 6 18 12 7 5 16 5 3 6 0 9 11 9 9 7 11 7 7 8 9 9 5 e 2 7 12 21 15 11 7 17 6 6 10 9 0 6 6 4 8 10 8 5 10 4 12 7 e 3 11 10 15 11 8 8 12 8 9 8 11 6 0 12 6 14 12 8 10 16 3 13 7 e 12 7 15 25 19 15 9 22 8 8 14 9 6 12 0 7 4 9 9 3 6 9 11 10 e 5 8 11 19 13 10 5 16 5 6 10 9 4 6 7 0 9 7 5 5 11 4 9 5 e 17 6 13 25 18 14 9 22 8 7 13 7 8 14 4 9 0 10 9 4 2 11 10 9 e 1911 13 22 15 13 7 21 7 9 14 11 10 12 9 7 10 0 5 7 11 10 5 9 e 23 9 9 18 10 9 4 16 4 6 9 7 8 8 9 5 0 6 11 7 4 4 e 29 5 12 22 16 12 6 20 5 5 11 7 5 10 3 5 4 7 6 0 6 8 9 7 e 35 7 15 26 19 15 11 24 9 9 14 8 10 16 6 11 2 11 11 6 0 13 11 11 e 37 9 10 17 13 9 7 14 7 7 9 9 4 3 9 4 11 10 7 8 13 0 12 6 i 2011 10 20 11 11 7 19 7 9 11 9 12 13 11 9 10 5 4 9 11 12 0 7 i 34 7 6 16 9 6 4 14 4 5 6 5 7 7 10 5 9 9 4 7 11 6 7 0 Actual dist from each F=7 to each F=10 is >=4. F-gap from F=6 to F=11 >=4. F-gap from F=6 to F=10>=4. Separate at F=8. 5 to CLUS 2. 1<8. 5 (2 ver, 43 vir) and CLUS 2. 2>8. 5 (44 ver, 4 vir) Dot gp>=4 CLUS 2 p=nnnn p=aaan q=xxxx q=aaax 0 2 Sparse lower end 0 3 3 2 1 3 i 32 i 18 i 19 i 23 i 6 i 36 F 4 1 i 32 0 2 8 4 13 11 9 9 0 5 1 i 18 4 3 2 0 12 10 8 10 0 7 1 i 19 13 12 4 6 0 4 5 9 3 9 2 i 23 11 10 5 5 4 0 3 7 3 10 1 i 6 6 5 9 8 5 3 0 5 4 11 1 i 36 9 10 7 11 9 7 5 0 5 12 1 i 32 and i 18 gap>=4 outliers 8 2 13 2 9 4 14 1 10 12 15 3 11 8 16 4 12 13 17 3 13 5 18 2 14 3 19 8 15 7 20 2 21 3 22 1 23 4 24 5 25 4 26 5 Thin area: (40 44) 27 5 36 37 37 38 38 40 42 43 44 44 45 45 45 47 28 4 e 4 i 7 e 10 e 31 e 32 s 14 i 39 s 16 s 19 e 49 s 15 e 44 e 11 e 8 s 6 s 34 F So, two rounds of Dotpd(y) gap analysis yields 29 3 e 4 0 9 5 3 4 34 29 11 35 9 8 10 29 34 37 30 2 i 7 9 0 8 11 12 38 30 39 35 16 40 14 13 14 34 39 37 CLUS 1 (50 Setosa, plus 4 Versicolor) 31 2 e 10 5 8 0 5 6 32 23 31 27 10 33 8 9 8 27 32 38 32 2 e 31 3 11 5 0 1 32 23 31 27 9 32 7 7 8 27 31 38 33 4 CLUS 2. 1 (43 Virginica, plus 2 Versicolor) e 32 4 12 6 1 0 31 22 30 25 8 31 6 7 7 26 30 38 34 5 s 14 34 38 32 32 31 0 25 20 17 23 18 26 28 25 16 17 38 36 3 i 39 24 30 23 23 22 25 0 20 17 17 20 21 24 21 18 21 40 CLUS 2. 2 (44 Veriscolor, plus 4 Virginica) 37 2 s 16 34 39 31 31 30 20 20 0 6 26 5 29 33 29 6 4 42 38 4 s 19 29 35 27 27 25 17 17 6 0 21 6 24 27 24 3 5 43 and picks out 3 Virginica, 4 Setosa as outliers 40 1 e 49 11 16 10 9 8 23 17 26 21 0 26 4 7 4 21 25 44 42 1 s 15 35 40 33 32 31 18 20 5 6 26 0 29 33 29 7 4 44 (More outliers would result by applying 1. 1 to the 43 1 e 44 9 14 8 7 6 26 21 29 24 4 29 0 4 1 24 28 45 44 2 e 11 8 13 9 7 7 28 24 33 27 7 33 4 0 5 27 32 45 45 5 sparse ends of the 2 nd round? ). e 8 10 14 8 8 7 25 21 29 24 4 29 1 5 0 23 28 45 47 6 s 6 29 34 27 27 26 16 18 6 3 21 7 24 27 23 0 5 45 48 3 Round 1: p=nnnn (n=min) and q=xxxx (x=max) s 34 34 39 32 31 30 17 21 4 5 25 4 28 32 28 5 0 45 49 4 So i 39, s 16, s 19, s 49, s 15 are "thin area" outliers AND s 14 is also. 50 6 Round 2: p=aaan (a=avg) and q=aaax 51 4 Separate at 42, giving CLUS 1<41 (50 Setosa, 4 Versicolor, e 8, e 11, e 44, e 49) and CLUS 2>=41. 52 3 53 5 54 3 55 5 56 1 Sparse Ends analysis should accomplish the same outlier detection that a few steps of 57 1 Sparse upper end 58 2 s 23 s 43 s 9 s 39 s 42 s 14 F SL accomplishes. If an outlier is surrounded at a fixed distance then those neighbors 59 1 s 23 0 5 8 7 13 7 56 60 1 s 43 5 0 3 2 9 3 57 will show up as sparse end neighbors and the outlier-ness of the point will be detected s 9 8 3 0 1 6 3 58 s 39 7 2 1 0 7 2 58 by looking at pairwise distances of that sparse end. s 42 13 9 6 7 0 8 59 s 14 7 3 3 2 8 0 60 no gap>4 outliers

CLUS 1 Sparse low end (check [0, 9] p=nxnn 0 2 4 6 6 9 10 q=xnxx i 23 i 6 i 36 i 8 i 31 i 3 i 26 0 1 2 3 3 4 4 4 4 5 6 6 6 6 7 7 i 23 0 3 7 6 7 10 10 Dotgp>=4 2 1 i 18 i 19 i 10 i 37 i 5 i 6 i 23 i 32 i 44 i 45 i 49 i 25 i 8 i 15 i 41 i 21 i 33 i 29 i 4 i 3 i 16 i 6 3 0 5 5 6 9 8 p=xnnn 4 1 i 1 0 17 18 10 4 5 15 17 18 6 5 6 6 13 11 6 7 7 8 9 9 7 i 36 7 5 0 7 5 7 7 q=nxxx 6 2 i 18 17 0 12 9 18 17 8 10 4 13 15 20 15 11 27 17 14 20 20 20 13 20 i 8 6 5 7 0 3 5 4 0 1 9 1 i 19 18 12 0 14 21 17 5 4 13 15 17 23 17 9 26 17 16 19 19 20 12 21 i 31 7 6 5 3 0 5 5 1 1 10 1 i 10 10 9 14 0 11 10 10 12 9 6 7 13 8 10 19 9 7 13 13 14 8 12 i 3 10 9 7 5 5 0 4 2 1 11 2 i 37 4 18 21 11 0 5 17 19 19 6 4 2 5 14 9 5 6 6 7 8 10 4 i 26 10 8 7 4 5 4 0 3 2 12 2 i 5 5 17 17 10 5 0 14 15 17 4 5 6 4 10 10 4 5 3 3 5 6 6 i 3, i 26, i 36 >=4 singleton outliers 4 7 13 3 i 6 15 8 5 10 17 14 0 3 9 11 14 19 13 5 24 14 12 16 16 17 9 18 {i 23, i 6}, {i 8, i 31} doubleton ols 5 1 14 3 i 23 17 10 4 12 19 15 3 0 11 13 16 21 15 6 25 16 14 17 17 18 10 20 6 7 15 2 i 32 18 4 13 9 19 17 9 11 0 14 16 20 15 11 27 17 14 20 20 20 12 20 7 5 16 2 i 44 6 13 15 6 6 4 11 13 14 0 3 8 3 9 13 3 2 6 7 8 4 7 8 9 17 4 i 45 5 15 17 7 4 5 14 16 16 3 0 6 4 12 12 2 3 7 7 9 7 5 9 3 18 3 i 49 6 20 23 13 2 6 19 21 20 8 6 0 6 16 8 7 7 7 11 3 10 7 19 3 i 25 6 15 17 8 5 4 13 15 15 3 4 6 0 10 12 4 3 6 6 6 5 5 11 3 20 2 i 8 13 11 9 10 14 10 5 6 11 9 12 16 10 0 20 11 9 12 12 12 5 15 12 5 21 5 i 15 11 27 26 19 9 10 24 25 27 13 12 8 12 20 0 11 13 8 8 9 16 8 13 4 22 6 i 41 6 17 17 9 5 4 14 16 17 3 2 6 4 11 11 0 3 5 5 7 6 4 14 5 23 5 i 21 7 14 16 7 6 5 12 14 14 2 3 8 3 9 13 3 0 7 7 8 4 6 15 4 Sparse hi end (checking [34, 43] 24 2 i 33 7 20 19 13 6 3 16 17 20 6 7 7 6 12 8 5 7 0 1 4 8 5 16 8 34 35 36 36 37 37 39 41 42 43 25 7 i 29 8 20 19 13 7 3 16 17 20 7 7 7 6 12 8 5 7 1 0 3 8 5 17 4 e 20 e 31 e 10 e 32 e 15 e 30 e 11 e 44 e 8 e 49 26 3 i 4 9 20 20 14 8 5 17 18 20 8 9 7 6 12 9 7 8 4 3 0 9 7 18 7 e 20 0 2 5 3 5 4 9 9 9 10 27 2 i 3 9 13 12 8 10 6 9 10 12 4 7 11 5 5 16 6 4 8 8 9 0 10 19 3 e 31 2 0 5 1 6 4 7 7 8 9 28 2 i 16 7 20 21 12 4 6 18 20 20 7 5 3 5 15 8 4 6 5 5 7 10 0 20 5 e 10 5 5 0 6 5 8 9 8 8 10 29 1 i 26 11 11 13 8 12 9 8 10 10 6 9 13 7 4 18 9 7 11 10 10 4 12 21 1 e 32 3 1 6 0 6 3 7 6 7 8 30 3 i 36 14 10 9 8 15 12 5 7 9 9 11 17 11 7 22 11 9 14 14 16 7 15 22 4 e 15 5 6 0 4 11 9 10 9 31 3 i 38 9 19 20 13 7 5 17 18 19 8 8 6 5 12 10 7 7 5 4 2 9 5 23 1 e 30 4 4 8 3 4 0 9 8 8 8 32 7 i 1, i 18, i 19, i 10, i 37, i 32 >=4 outliers 24 1 e 11 9 7 11 9 0 4 5 7 33 4 gap: (24, 31) CLUS 1<27. 5 (50 versi, 49 virg) CLUS 2>27. 5 (50 set, 1 virg) 31 2 e 44 9 7 8 6 9 8 4 0 1 4 34 1 33 2 e 8 9 8 8 7 10 8 5 1 0 4 35 1 34 12 Sparse hi end (checking [38, 39] e 49 10 8 9 8 7 4 4 0 36 2 35 8 38 38 39 39 e 30, e 49, ei 15, e 11 >=4 singleton ols 37 2 36 17 s 42 s 36 s 37 s 1 {e 44, e 8} doubleton ols 39 1 Thinning (8, 13) 37 6 s 42 0 10 16 21 41 1 CLUS 1 Split in middle=10. 5 38 2 s 36 10 0 6 11 42 1 Dotgp>=4 CLUS_1. 1<10. 5 (21 virg, 2 ver) 39 2 s 37 16 6 0 6 43 1 p=nnnn CLUS_1. 2>10. 5 (12 virg, 42 ver) s 15 21 11 6 0 q=xxxx Clus 1 s 37, s 1 outliers 0 1 p=nnxn Sparse hi end (checking [10, 13] Thinning (7, 9) 1 2 q=xxnx 10 10 11 11 13 13 Split in middle=7. 5 2 2 0 2 CLUS 1 e 34 i 2 i 14 i 43 e 41 i 20 i 7 i 35 CLUS_1. 2. 1 < 7. 5 (10 virg, 4 ver) 3 1 1 1 Dotgp>=4 CLUS 1. 2 e 34 0 4 5 4 10 5 13 6 CLUS_1. 2. 2 > 7. 5 ( 1 virg, 38 ver) 4 2 2 5 p=nnnx Dotgp>=4 i 2 4 0 3 0 10 7 11 8 i 15 gap>=4 outlier at F=0 5 1 3 8 q=xxxn p=aaan hi end gap outlier i 30 i 14 5 3 0 3 10 7 10 9 6 6 4 9 CLUS 1. 2. 1 0 1 q=aaax i 43 4 0 3 0 10 7 11 8 7 2 5 6 Dotgp>=4 4 1 CLUS 1. 2. 1 0 1 e 41 10 10 0 9 8 14 8 3 6 9 p=anaa 5 3 Dotgp>=4 4 4 i 20 5 7 7 7 9 0 13 7 9 1 7 14 q=axaa 6 5 p=aana 5 3 i 7 13 11 10 11 8 13 0 17 10 2 8 11 0 1 7 4 q=aaxa 6 3 i 35 6 8 9 8 14 7 17 0 11 2 9 7 1 1 8 3 0 5 7 4 i 7, i 35 >=4 singleton outliers 12 2 10 4 2 1 9 6 1 2 8 1 13 6 11 2 4 2 10 7 2 3 9 5 14 6 13 2 6 3 11 3 3 2 10 7 15 7 7 4 12 4 4 1 11 3 16 2 C. 2. 1 0 0 1 2 3 3 4 4 5 5 6 7 9 2 13 8 6 1 12 5 i 24 e 7 i 34 i 47 i 28 e 34 e 36 e 21 i 50 i 2 i 43 i 14 i 22 17 2 14 4 13 3 i 24 0 7 4 2 2 4 4 9 6 5 5 5 7 7 18 3 15 4 14 6 e 7 7 0 6 9 6 5 8 4 5 7 9 9 11 10 19 3 CLUS 1. 2. 1 16 3 i 34 4 6 0 5 4 5 3 9 7 5 6 6 8 9 15 1 20 2 p=naaa 17 8 i 47 2 9 5 0 4 6 5 11 8 7 5 5 6 8 16 4 21 2 q=xaaa i 27 2 6 4 4 0 2 4 7 5 5 6 6 18 5 17 1 22 3 0 4 i 28 4 5 5 6 2 0 4 6 3 3 5 5 7 6 19 3 18 1 e 34 4 8 3 5 4 4 0 9 6 4 4 4 5 6 23 4 1 1 20 1 19 2 e 36 9 4 9 11 7 6 9 0 4 8 10 10 11 9 24 2 2 1 21 1 e 21 6 5 7 8 5 3 6 4 0 4 6 6 8 5 25 1 3 2 22 3 i 50 5 7 5 3 4 8 4 0 3 3 6 5 26 2 4 2 23 1 i 2 5 9 6 5 5 5 4 10 6 3 0 0 3 3 27 3 5 2 i 43 5 9 6 5 5 5 4 10 6 3 0 0 3 3 28 1 6 1 i 14 7 11 8 6 6 7 5 11 8 6 3 3 0 3 i 22 7 10 9 8 6 6 6 9 5 5 3 3 3 0 29 1 7 1 DG-SE (other corners) Check Dot (y) gaps>=4 Sparse low end (checking [0, 7] p, d Check sparse ends.

Check Dotp, d(y) for thinnings. Calc AVG of each side of thinning as p, q. redo. Dot p=nnnn q=xxxx 0 2 3 2 4 1 5 1 7 1 9 2 10 1 11 1 12 1 13 2 14 1 15 3 16 4 17 3 18 2 19 8 20 2 21 3 22 1 23 4 24 5 25 4 26 5 27 5 28 4 29 3 30 2 31 2 32 2 33 4 34 5 36 3 37 2 38 4 40 1 42 1 43 1 44 2 45 5 47 6 48 3 49 4 50 6 51 4 52 3 53 5 54 3 55 5 56 1 57 1 58 2 59 1 60 1 Dot p=AVG>22 q=AVG<22 0 1 1 1 2 2 3 2 4 3 5 6 6 7 7 10 8 9 9 3 10 3 11 2 12 1 19 1 23 1 24 2 26 1 29 1 30 1 31 2 32 2 33 2 34 4 35 2 36 5 37 1 38 3 39 2 40 3 41 4 42 4 43 2 44 3 45 6 46 7 47 2 48 3 49 1 50 3 52 7 53 1 54 4 55 1 56 3 57 3 58 2 59 2 61 1 62 1 63 1 64 1 66 1 67 1 68 1 69 1 70 1

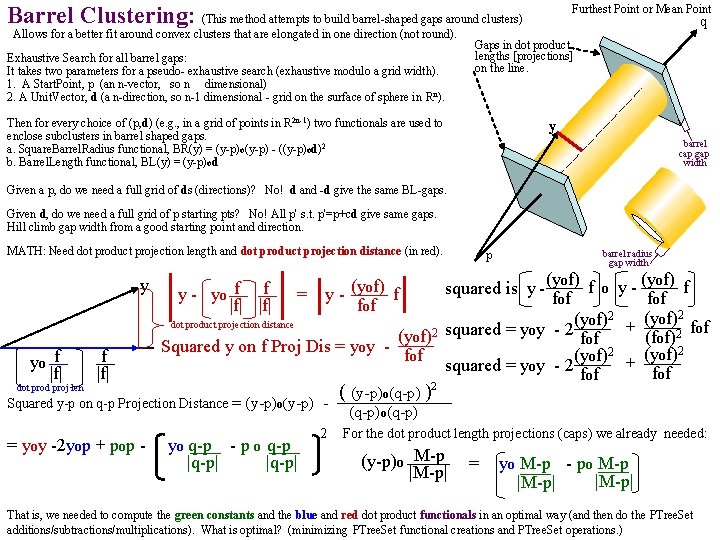
Barrel Clustering: (This method attempts to build barrel-shaped gaps around clusters) Allows for a better fit around convex clusters that are elongated in one direction (not round). Exhaustive Search for all barrel gaps: It takes two parameters for a pseudo- exhaustive search (exhaustive modulo a grid width). 1. A Start. Point, p (an n-vector, so n dimensional) 2. A Unit. Vector, d (a n-direction, so n-1 dimensional - grid on the surface of sphere in Rn). Furthest Point or Mean Point q Gaps in dot product lengths [projections] on the line. Then for every choice of (p, d) (e. g. , in a grid of points in R 2 n-1) two functionals are used to enclose subclusters in barrel shaped gaps. a. Square. Barrel. Radius functional, BR(y) = (y-p)o(y-p) - ((y-p)od)2 b. Barrel. Length functional, BL(y) = (y-p)od y barrel cap gap width Given a p, do we need a full grid of ds (directions)? No! d and -d give the same BL-gaps. Given d, do we need a full grid of p starting pts? No! All p' s. t. p'=p+cd give same gaps. Hill climb gap width from a good starting point and direction. MATH: Need dot product projection length and dot product projection distance (in red). y yo f |f| dot prod proj len f |f| p barrel radius gap width (yof) f o y - (yof) f = fof (yof)2 + (yof)2 fof dot product projection distance (yof)2 squared = yoy - 2 fof (fof)2 Squared y fon f Proj Dis = yoy (yof)2 + (yof)2 fof squared = yoy - 2 fof y - yo f f |f| y - (yof) f fof Squared y-p on q-p Projection Distance = (y-p)o(y-p) 1 st = yoy -2 yop + pop - ( yo(q-p) - p o(q-p |q-p| 2 squared is y - ( (y-p)o(q-p) )2 (q-p)o(q-p) For the dot product length projections (caps) we already needed: (y-p)o M-p |M-p| = ( yo(M-p) - po M-p ) |M-p| That is, we needed to compute the green constants and the blue and red dot product functionals in an optimal way (and then do the PTree. Set additions/subtractions/multiplications). What is optimal? (minimizing PTree. Set functional creations and PTree. Set operations. )

4 functionals in the dot product group of gap clusterers on a Vector. Space subset, Y (y Y): 1. SLp(y) = (y-p)o(y-p), p a fixed vector. Square Length functional primarily for outlier identification and densities. 2. Dotd(y) = yod, (d is a unit vector) the Dot-product functional. Using d=q-p/|q-p| and y-p y y y - (yod)d = projection. Squaring its y - (yod)d Dotp, q(y) = (y-p)o(q-p)/|q-p| 2 length: (y-yodd)o(y-yodd)=yoy-(yod) so again yoy (yod)2 = squared proj d yod projection (neg) d 3. SPDd(y) = yoy - (yod)2 (d a unit vector) is the Square Projection Distance functional 2 ( (y-p) o(q-p) ) E. g. , if d ≡ (q-p)/|q-p|, d = unit vector from vector p to vector q, then SPD(y)= (y-p)o(y-p) (q-p)o(q-p) But to avoid creating an entirely new Vector. PTree. Set(Y-p) 2 for the space (with origin shifted to p), we think it useful q-p to alter the expression to : SPDpq(y) = yoy -2 yop + pop - yo - po |q-p| where we might: 1 st compute the constant vector q-p 2 nd the Scalar. PTree. Set yo q-p |q-p| q-p 3 rd the constant po |q-p| 5 th the SPTree. Set yo q-p - po q-p |q-p| 7 th the SPTree. Sets yoy, yop |q-p| 4 th the SPTree. Set yo q-p - po q-p |q-p| 6 th the constant pop q-p po |M-p| 8 th the SPTree. Set= yoy -2 yop + pop - yo |M-p| Is it better to leave all the additions and subtractions for one mega-step at the end? Other efficiency thoughts? We note that Dot(y)=yod shares many construction steps with SPD. (y-p)o q-p |q-p| = yo q-p po |q-p| 4. CAd(y) = yod/|y|, (d unit vector) the Cone Angle functional. Using d=q-p/|q-p| and y=x-p CAp, q(y) = (y-p)od/|y-p| SCAp, q(y) = (y-p)od 2/|y-p|2 = (y-p)od 2/(y-p)o(y-p), Squared Cone Angle functional 2

SPD p 64 29 50 17 q 61 29 45 14 e 14 V Ct 1 6 2 4 3 8 4 4 5 10 6 2 7 2 8 2 9 7 10 2 11 2 12 2 13 1 15 2 17 1 18 4 19 2 20 4 22 1 24 1 25 1 26 1 29 1 31 2 32 2 33 3 37 2 i 15 i 36 92 1 i 32 SPD p 54 22 39 10 q 70 34 51 18 V Ct 2 8 3 10 4 10 5 10 6 5 thin gap 7 10 8 6 9 8 10 6 11 1 masking V>6: Total_e 37 2 Masked_e Total_i 37 29 Masked_i However I cheated a bit. I used p=Min. Vect(e) and q=Max. Vect(e) which makes it somewhat supervised. START OVER WITH THE FULL 150 ---------> SPD p 64 29 50 17 q 61 29 45 14 e 14 V Ct 2 10 3 12 mask: V<8. 5 4 12 CTs 50 0 SMs 5 12 CTe 50 50 SMe 6 8 CTi 50 24 SMi 7 11 CLUS 1 8 9 9 5 mask: 8. 5<V<15. 5 10 9 CTs 50 1 SMs 11 4 CTe 50 0 SMe 12 4 CTi 50 24 SMi 13 2 14 1 CLUS 2 17 2 18 3 19 10 20 5 mask: V>15. 5: 21 6 CTs 50 49 SMs 22 5 CTe 50 0 SMe 23 6 CTi 50 2 SMi 24 6 This tube contains 25 3 49 setosa 27 2 + 2 virginica 29 2 30 1 CLUS 3 SPD on CLUS 1 p 50 20 35 10 e 11 q 58 31 37 12 =MN V Ct 2 3 3 4 mask: V<12. 5 5 SMe 4 5 5 7 24 SMi 6 2 CLUS 1. 1 7 2 8 6 9 6 10 3 11 4 12 2 13 4 14 4 15 3 mask: V>12. 5 16 2 45 SMe 17 1 0 SMi 18 5 CLUS 1. 2 19 1 20 2 22 2 23 1 24 1 25 1 26 1 29 1 CLUS 1. 2 is pure Versicolor (45 of the 50). CLUS 3 is almost pure Setosa (49 of the 50, plus 2 virginica) CLUS 2 is almost purely [1/2 of] viriginica (24 of 50, plus 1 setosa). CLUS 1. 1 is the other 24 virginicas, plus the other 5 versicolors. So this method clusters IRIS quite well (albeit into 4 clusters, not three). Note that caps were not put on these tubes. Also, this was NOT unsupervised clustering! I took advantage of my knowledge of the classes to carefully chose the unit vector points, p and q E. g. , p = Min. Vector(Versicolor) and q = Max. Vector(Versicolor. True, if one sequenced thru a fine enough d-grid of all unit vectors [directions], one would happen upon a unit vector closely aligned to d=q-p/|q-p| but that would be a whole lot more work that I did here (would take much longer). In worst case though, for totally unsupervised clustering. there would be no other way than to sequence through a grid of unit vectors. However, a good heuristic might be to try all unit vectors "corner-to-corner" and "middle-of-face-TO-middle-of-opposite-face" first, etc. Another thought would be to try to introduce some sort of hill climbing to "work our way" toward a good combination of a radial gap plus two good linear cap gaps for that radial gap.

SPD p 58 44 69 25 axxx q 58 30 37 11 aaaa V Ct. 2 1 3 5 4 6 mask: V<11. 5 5 6 0 SM setosa 6 8 46 SM versicolor 7 6 24 SM virginica 8 8 CLUS 1 9 15 10 7 11 8 12 13 13 8 mask: V>11. 5 14 14 50 SM setosa 4 SM versicolor 15 9 16 13 26 SM virginica CLUS 2 17 6 18 4 19 4 20 3 21 4 23 1 25 1 SPD on CLUS 1 69 28 46 25 C 11 xaax 60 28 46 15 C 11 aaaa V Ct 1 2 2 3 3 4 4 8 5 8 6 14 7 8 8 4 9 5 10 6 11 1 12 3 14 1 15 2 17 1 no thins SPD on CLUS 1 p 60 34 60 25 C 1 US 1 axxx q 60 28 46 15 C 1 US 1 aaaa V Ct. 1 3 2 5 3 9 4 13 5 18 6 12 7 4 8 1 9 2 11 3 no thinnings SPD on CLUS 1 p 69 28 60 25 C 1 US 1 xaxx q 60 28 46 15 C 1 US 1 aaaa V Ct. 1 4 mask: V<3. 5 2 13 14 SM versi 3 7 10 SM virgi CL 1. 1? 4 19 mask: V>3. 5 5 9 0 SM setosa 6 7 32 SM versi 7 9 14 SM virgi 8 2 CLUS 1. 2? SPD on CLUS 2 p 56 44 69 25 C 1 US 2 axxx q 56 32 29 9 C 1 US 2 aaaa V Ct. 6 2 7 2 mask: V<13. 5 8 6 44 SM setosa 9 13 0 SM versicolor 10 7 02 SM virginica 11 7 CLUS 2. 1 12 4 13 5 14 11 15 9 mask: 100>V>13. 5 16 2 6 SM setosa 18 4 4 SM versicolor 21 2 24 SM virginica 22 1 CLUS 2. 2 23 3 25 1 26 1 SPD on CLUS 1 69 28 60 15 C 11 xaxa 60 28 46 15 C 11 aaaa V Ct 1 2 2 3 3 12 4 12 5 10 6 15 7 7 8 4 9 1 10 2 11 1 12 1 no thins SPD on CLUS 1 p 69 34 60 15 C 1 US 1 xxxa q 60 28 46 15 C 1 US 1 aaaa V Ct. 1 1 2 3 3 10 4 15 5 16 6 12 7 7 8 3 9 1 10 1 11 1 no thinnings SPD on CLUS 1 p 60 34 46 25 C 1 US 1 axax SPD on CLUS 1 q 60 28 46 15 C 1 US 1 aaaa p 60 34 60 15 C 1 US 1 axxa V Ct. q 60 28 46 15 C 1 US 1 aaaa 1 1 V Ct. 2 3 1 1 3 4 mask: V<9. 5 2 2 4 2 3 6 5 12 37 SM vers 4 9 6 13 16 SM virg CL 1. 1? 5 12 7 9 8 7 6 17 9 2 7 8 10 7 mask: V>9. 5 8 6 11 4 9 SM vers 9 5 13 2 8 SM virg CL 1. 2? 10 1 14 1 11 1 17 2 12 2 no thinnings 18 1 C 11 axaa C 11 aaaa SPD on C 11 xaaa C 11 aaxa C 11 aaax V Ct C 11 aaaa 1 2 mask: V<5. 5 V Ct 2 2 16 ver 1 3 1 2 3 2 2 4 3 vir. CL 1. 1? 2 1 2 3 4 10 3 5 3 3 3 6 4 9 5 3 4 4 5 10 4 12 5 12 6 13 6 9 6 15 5 11 7 8 mask: V>5. 5 7 4 7 5 6 9 8 7 30 ver 8 5 8 6 7 11 9 4 21 vir. CL 1. 1? 9 4 9 2 8 5 10 3 10 7 10 6 9 5 11 6 11 4 11 3 10 1 12 2 12 1 13 1 11 3 13 2 14 1 13 2 14 2 15 1 17 2 15 2 17 1 18 1 17 2 18 1 19 1 SPD on CLUS 1 p 60 28 60 25 C 11 aaxx q 60 28 46 15 C 11 aaaa V Ct. 1 1 2 7 3 10 4 13 5 13 6 13 7 6 8 2 9 2 11 1 12 2 no thinnings SPD on CLUS 1 69 28 46 25 C 11 xxaa 60 28 46 15 C 11 aaaa V Ct 1 1 mask: V<5. 5 2 4 26 ver 3 6 4 vir CL 1. 1? 4 9 5 10 6 7 mask: V>5. 5 7 9 20 ver 8 5 20 vir CL 1. 1? 9 3 10 4 11 2 12 4 13 1 14 3 17 2 SPD on CLUS 1 p 69 34 46 25 C 1 US 1 xxax q 60 28 46 15 C 1 US 1 aaaa V Ct. 1 1 2 4 3 3 4 9 5 9 6 14 7 9 8 4 9 6 10 3 11 3 12 1 14 2 15 1 16 1 no thinnings

x=s 15 58 40 12 2 (58=avg(y 1) ) V Ct 0 3 s 15, s 17, s 34 1 12 s 6, 11, 16, 19, 20, 22, 28, 32, 3337, 49 2 12 s 1, 10 13, 18, 21, 27, 29, 40, 41, 44, 45, 50 3 7 s 2, 12, 23, 24, 35, 36, 38 4 10 s 2, 3, 7, 13, 25, 26, 30, 31, 46, 48 5 2 s 4, s 43 6 2 s 9, s 39 7 1 s 14 8 1 i 39 9 1 s 32 ^^all 50 setosa + i 39 14 1 e 49 16 2 17 2 19 1 1. (y-p)o(y-p) remove edge 20 2 outliers ( thr>2*50) 21 5 2. lthin gaps in SPD: d, 22 4 from an edge point to MN. 23 3 24 4 3 For each thin PL, do len 25 1 gap anal of pts in " tube". 27 8 28 2 29 2 30 4 31 1 32 4 34 2 35 2 36 2 37 3 38 2 39 2 40 4 41 1 43 2 44 4 45 2 46 1 47 2 48 1 50 4 52 2 53 2 54 2 56 2 57 1 58 1 i 1 62 1 i 31 vv 9 virginica 63 1 i 10 64 1 i 8 66 1 i 36 69 1 i 32 74 1 i 16 76 1 i 18 77 1 i 23 85 1 i 19 But here I mistakenly used the mean rather than the max corner. So I will redo - but note the high level of cluster and outlier revelation? ? ? i 18 77 38 67 22 p i 32 79 38 64 20 p i 19 77 26 69 23 p max 79 38 69 25 max 79 44 69 25 V Ct 0 2 0 2 1 2 2 6 1 1 2 2 3 3 5 4 4 3 3 4 3 5 4 4 4 5 3 6 2 5 2 6 4 7 6 6 6 7 4 8 9 7 3 8 7 9 2 8 5 9 2 10 2 9 4 10 3 11 2 10 4 11 1 12 5 11 2 12 4 13 7 12 3 13 5 14 2 13 4 14 4 15 6 14 6 15 7 95 remaining versicolor 16 2 15 4 16 2 and virginica=Sub. Clus 1. 17 5 16 1 17 5 19 3 17 7 18 3 Continue outlier id rounds 20 2 18 2 19 1 on SC 1 (max. SL, max. SW, 22 3 19 3 20 1 max PW) then do "capped 23 2 20 2 21 4 tube" (further subclusters. ) 24 3 22 2 23 2 25 2 23 1 24 2 26 1 24 2 25 4 e 13 i 7 e 40 e 4 e 10 F 27 1 25 4 26 1 6 10 28 28 1 26 4 27 2 e 13 0 14 7 9 8 29 29 3 27 1 28 1 i 7 14 0 9 2 4 29 30 1 28 2 29 2 e 40 7 9 0 e 32 e 11 e 8 e 44 e 49 6 9 2 0 5 30 31 2 29 2 30 1 e 4 e 32 0 7 7 6 8 5 0 32 32 1 e 32 30 1 32 1 e 10 10 8 4 e 11 7 0 5 4 7 42 1 e 11 32 2 e 8 7 5 0 1 4 43 2 e 8, 44 33 1 {e 4, e 40} form a doubleton outlier set e 44 6 4 1 0 4 44 1 e 49 34 1 i 7 and e 10 are singleton outliers e 49 8 7 4 4 0 51 1 i 39 35 1 60 1 No new outliers reviealed 61 1 SPD(y) =(y-p)o(y-p)-(y-p)od 2 d: mn-mx 62 1 V Ct 63 1 Next slide 64 1 65 1 i 1 63 33 60 25 p 66 1 max 79 38 69 25 67 3 V Ct 68 4 0 2 69 4 1 10 45 remaining setosa. 70 3 2 11 This is Sub. Cluster 2 71 3 3 6 (may have additional 72 4 4 15 outliers or sub 73 2 5 4 subclusters but we 74 5 6 8 will not analyse 75 1 7 9 further (would be 76 2 8 4 done in practice tho 77 1 9 5 78 3 10 2 s 3 s 9 s 39 s 43 s 42 s 23 79 1 11 7 s 3 0 4 4 3 9 5 80 1 s 3 e 13 e 20 e 15 e 31 e 32 e 30 F 13 4 s 9 4 0 1 3 6 8 83 1 s 9 e 13 0 5 9 6 6 7 15 14 2 s 39 4 1 0 2 7 7 84 2 s 39, 43 s 43 3 3 2 0 e 20 5 2 3 4 15 15 2 9 5 85 1 s 42 e 15 9 5 0 6 6 4 16 16 1 s 42 9 6 7 9 0 13 87 1 s 23 e 31 6 2 6 0 1 4 17 17 1 s 23 5 8 7 5 13 0 91 1 s 14 e 32 6 3 6 1 0 3 18 18 1 e 30 7 4 4 4 3 0 19 19 1 2 actual gap-ouliers, checking distances reveals e 30, e 15 outliers 4 e-outlier (versicolor), 5 s-outliers (setosa). e 20, e 31, e 32 form SC 12 Declared tripleton outlier set? (But they are not singleton outliers. )

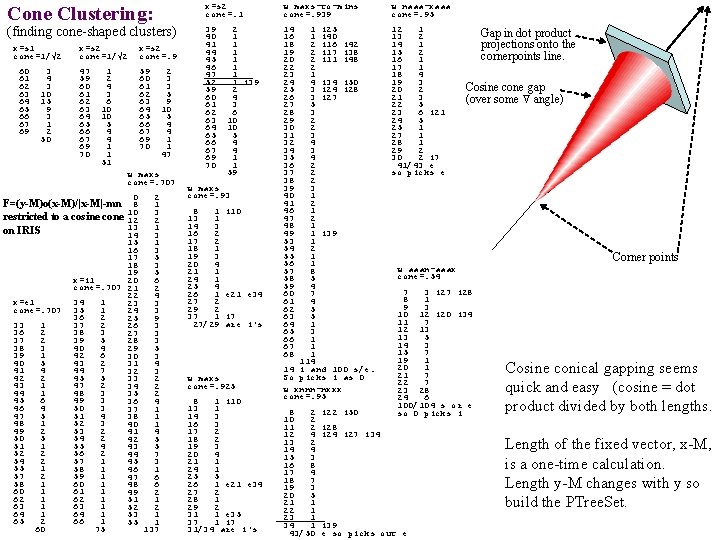
Cone Clustering: (finding cone-shaped clusters) x=s 1 cone=1/√ 2 60 61 62 63 64 65 66 67 69 3 4 3 10 15 9 3 1 2 50 x=s 2 cone=1/√ 2 x=s 2 cone=. 9 47 59 60 61 62 63 64 65 66 67 69 70 1 2 4 3 6 10 10 5 4 4 1 1 51 2 3 3 5 9 10 5 4 4 1 1 47 w maxs cone=. 707 0 2 F=(y-M)o(x-M)/|x-M|-mn 8 1 3 restricted to a cosine cone 10 12 2 13 1 on IRIS 14 3 15 1 16 3 17 5 18 3 19 5 x=i 1 20 6 cone=. 707 21 2 22 4 x=e 1 34 1 23 3 cone=. 707 35 1 24 3 36 2 25 9 33 1 37 2 26 3 36 2 38 3 27 3 37 2 39 5 28 3 38 3 40 4 29 5 39 1 42 6 30 3 40 5 43 2 31 4 44 7 32 3 42 2 45 5 33 2 43 1 47 2 34 2 44 1 48 3 35 2 45 6 49 3 36 4 46 4 50 3 37 1 47 5 51 4 38 1 48 1 52 3 40 1 49 2 53 2 41 4 50 5 54 2 42 5 51 1 55 4 43 5 52 2 56 2 44 7 54 2 57 1 45 3 55 1 58 1 46 1 57 2 59 1 47 6 58 1 60 1 48 6 60 1 61 1 49 2 62 1 51 1 63 1 52 2 64 1 53 1 65 2 66 1 55 1 60 75 137 x=s 2 cone=. 1 w maxs-to-mins cone=. 939 w naaa-xaaa cone=. 95 39 40 41 44 45 46 47 52 59 60 61 62 63 64 65 66 67 69 70 14 16 18 19 20 22 23 24 25 26 27 28 29 30 31 32 34 35 36 37 38 39 40 41 46 47 48 49 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 12 1 13 2 14 1 15 2 16 1 17 1 18 4 19 3 20 2 21 3 22 5 23 6 i 21 24 5 25 1 27 1 28 1 29 2 30 2 i 7 41/43 e so picks e 2 1 1 1 1 i 39 2 4 3 6 10 10 5 4 4 1 1 59 w maxs cone=. 93 8 1 13 1 14 3 16 2 17 2 18 1 19 3 20 4 21 1 24 1 25 4 26 1 27 2 29 2 37 1 27/29 i 10 e 21 e 34 i 7 are i's w maxs cone=. 925 8 1 i 10 13 1 14 3 16 3 17 2 18 2 19 3 20 4 21 1 24 1 25 5 26 1 e 21 e 34 27 2 28 1 29 2 31 1 e 35 37 1 i 7 31/34 are i's 1 i 25 1 i 40 2 i 16 i 42 2 i 17 i 38 2 i 11 i 48 2 1 4 i 34 i 50 3 i 24 i 28 3 i 27 5 3 2 2 3 4 2 2 2 3 1 2 1 1 i 39 1 2 1 1 8 5 4 7 4 5 5 1 3 1 114 14 i and 100 s/e. So picks i as 0 w xnnn-nxxx cone=. 95 8 2 10 2 11 2 12 4 13 2 14 4 15 3 16 8 17 4 18 7 19 3 20 5 21 1 22 1 23 1 34 1 43/50 i 22 i 50 Gap in dot product projections onto the cornerpoints line. Cosine cone gap (over some angle) Corner points w aaan-aaax cone=. 54 7 3 i 27 i 28 8 1 9 3 10 12 i 20 i 34 11 7 12 13 13 5 14 3 15 7 19 1 20 1 21 7 22 7 23 28 24 6 100/104 s or e so 0 picks i i 28 i 24 i 27 i 34 i 39 e so picks out e Cosine conical gapping seems quick and easy (cosine = dot product divided by both lengths. Length of the fixed vector, x-M, is a one-time calculation. Length y-M changes with y so build the PTree. Set.

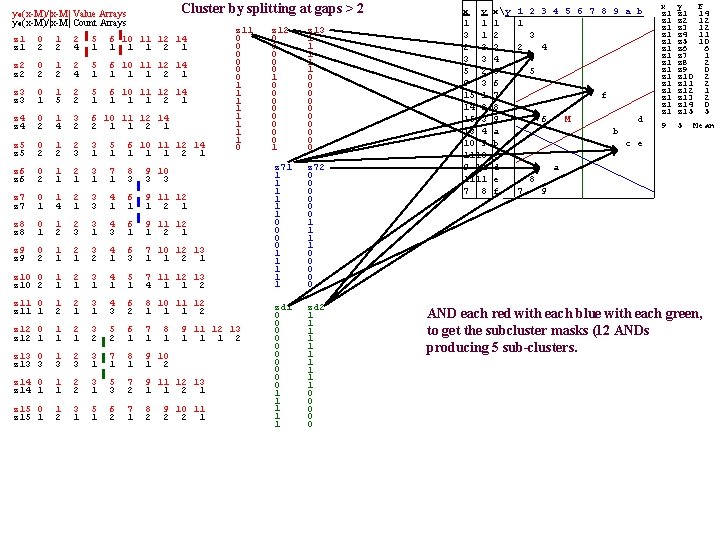
APPENDIX Fx. M(x, y)=yo(x-M)/|x-M|-min on X X≡{(x, y)|x, y X}, where X(x, y) is a Spaeth image table Cluster by splitting at all F_gaps > 2 The 15 Value_Arrays (one for each x) The 15 Count_Arrays z 1 z 2 z 3 z 4 z 3 z 5 z 6 z 7 z 8 z 4 z 9 z 10 z 11 z 5 z 12 z 13 z 14 z 6 z 15 z 7 z 8 z 9 0 1 2 5 6 10 11 12 14 0 2 0 5 0 6 0 10 0 11 0 12 0 14 1 0 0 0 0 1 0 0 5 0 0 1 12 0 0 0 2 0 0 6 0 1 11 0 0 14 0 0 0 0 0 1 0 3 1 6 0 10 0 11 0 12 0 14 0 0 1 0 0 0 0 1 0 2 1 3 0 5 0 6 0 10 0 11 0 12 0 14 0 0 1 0 0 0 0 0 0 0 0 1 0 2 0 3 1 7 0 8 0 9 0 10 0 0 Level 0, stride=z 1 Point. Set (as a p. Tree mask) 0 0 0 1 1 1 2 2 2 3 3 3 4 4 4 6 6 6 3 4 5 7 11 12 13 z 11 0 1 2 3 4 6 8 10 11 12 z 12 0 1 2 3 5 6 7 8 1 2 3 7 8 9 10 z 14 0 1 2 3 5 7 9 11 12 13 6 The FAUST algorithm: 7 1 1 2 1 z 2 2 2 4 1 1 2 1 z 3 1 5 2 1 1 2 1 z 4 2 2 1 1 2 1 z 5 2 2 3 1 1 1 z 6 2 1 1 3 3 3 z 7 1 4 1 3 1 1 1 2 1 z 8 1 2 3 1 1 2 1 z 9 2 1 1 2 1 3 1 1 2 1 z 10 2 1 1 1 4 1 1 2 z 11 1 2 1 1 3 2 1 1 1 2 z 12 1 1 1 2 2 1 1 1 z 13 3 1 1 2 z 14 1 1 2 1 3 2 1 1 2 1 z 15 1 2 1 2 2 2 1 y Fx. M z 1 z 1 z 1 z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 z 10 z 11 z 12 z 13 z 14 z 15 14 12 12 11 10 6 1 2 0 2 2 1 2 0 5 9 5 M (=Mean. Vector) p. Tree masks of the 3 z 1_clusters (obtained by ORing) 9 11 12 13 z 13 0 5 4 x 7 10 12 13 2 9 11 12 1 1 2 9 11 12 z 10 0 z 15 0 z 1 X x y y=1 2 3 4 5 6 7 8 9 a b 1 1 x=1 1 3 1 2 3 2 4 3 3 4 5 2 5 5 9 3 6 6 15 1 7 f 10: p 14 2 8 ga 15 3 9 6 M d 13 4 a b 10 9 b c e 5 -2 : p 1110 c ga 9 11 d a 1111 e 8 7 8 f 7 9 8 1 2 z 11 0 0 0 1 1 1 1 0 z 12 0 0 0 1 0 0 0 0 1 z 13 1 1 1 0 0 0 0 0 9 10 11 1. project onto each Mx line using the dot product with the unit vector from M to x. (only x=z 1 is shown) 2. Generate each Value Array, F[x 0]|(y), x X (also generate the Count_Arrays and the mask p. Trees). 3. Analyze all gaps and create sub-cluster p. Tree Masks.

Cluster by splitting at gaps > 2 yo(z 7 -M)/|z 7 -M| Value. Arrays yo(z 7 -M)/|z 7 -M| Count. Arrays z 1 0 2 1 2 2 4 5 1 6 10 11 12 14 1 1 1 2 1 z 2 0 2 1 2 2 4 5 1 6 10 11 12 14 1 1 1 2 1 z 3 0 1 1 5 2 2 5 1 6 10 11 12 14 1 1 1 2 1 z 4 0 2 1 4 3 2 6 10 11 12 14 2 1 1 2 1 z 5 0 2 1 2 2 3 3 1 5 1 6 10 11 12 14 1 1 1 2 1 z 6 0 2 1 1 2 1 3 1 7 1 8 3 9 10 3 3 z 7 0 1 1 4 2 1 3 3 4 1 6 1 9 11 12 1 z 8 0 1 1 2 2 3 3 1 4 3 6 1 9 11 12 1 z 9 0 2 1 1 2 1 3 2 4 1 6 3 7 10 12 13 1 1 2 1 z 10 0 z 10 2 1 1 2 1 3 1 4 1 5 1 7 11 12 13 4 1 1 2 z 11 0 z 11 1 1 2 2 1 3 1 4 3 6 2 8 10 11 12 1 1 1 2 z 12 0 z 12 1 1 1 2 1 3 2 5 2 6 1 7 1 z 13 0 z 13 3 1 3 2 3 3 1 7 1 8 1 9 10 1 2 z 14 0 z 14 1 1 1 2 2 3 1 5 3 7 2 9 11 12 13 1 1 2 1 z 15 0 z 15 1 1 2 3 1 5 1 6 2 7 1 8 2 8 1 z 11 0 0 0 1 1 1 1 0 9 11 12 13 1 1 1 2 9 10 11 2 2 1 z 12 0 0 0 1 0 0 0 0 1 z 13 1 1 1 0 0 0 0 0 z 71 1 1 1 0 0 1 1 1 z 72 0 0 0 1 1 0 0 0 x y 1 1 3 1 2 2 3 3 5 2 9 3 15 1 14 2 15 3 13 4 10 9 11 1111 7 8 xy 1 2 3 4 5 6 7 8 9 a b 1 1 2 3 3 2 4 4 5 5 6 7 f 8 9 g 6 M d ap: a b 6 -9 b c e c d a e 8 f 7 9 x z 1 z 1 z 1 z 1 y z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 z 10 z 11 z 12 z 13 z 14 z 15 9 5 F 14 12 12 11 10 6 1 2 0 2 2 1 2 0 5 Mean In Step_3 of the algorithm we can: Analyze one of the gap arrays (e. g. , As done for z 1. Subclusters is shown above) then start over on each subcluster. Or we can analyze all gap arrays concurrently (in parallel using the same F saving the [substantial? ] re-compute costs? ) and then intersect the subcluster partitions we get from each x_Value. Array gap analysis, forthe final subclustering. Here we use the second alternative, judiciously choosing only the x's that are likely to be productive (choosing z 7 next). Many are likely to produce redundant partitions - e. g. , z 1, z 2, z 3, z 4, z 6 - as their projection lines will be nearly coincident. How should we choose the sequence of "productive" strides? One way would be to always choose the remaining stride with the shortest Value. Array, so that the chances of decent sized gaps is maximized. Other ways of choosing?

Cluster by splitting at gaps > 2 z 1 0 2 1 2 2 4 5 1 6 10 11 12 14 1 1 1 2 1 z 2 0 2 1 2 2 4 5 1 6 10 11 12 14 1 1 1 2 1 z 3 0 1 1 5 2 2 5 1 6 10 11 12 14 1 1 1 2 1 z 4 0 2 1 4 3 2 6 10 11 12 14 2 1 1 2 1 z 5 0 2 1 2 2 3 3 1 5 1 6 10 11 12 14 1 1 1 2 1 z 6 0 2 1 1 2 1 3 1 7 1 8 3 9 10 3 3 z 7 0 1 1 4 2 1 3 3 4 1 6 1 9 11 12 1 z 8 0 1 1 2 2 3 3 1 4 3 6 1 9 11 12 1 z 9 0 2 1 1 2 1 3 2 4 1 6 3 7 10 12 13 1 1 2 1 z 10 0 z 10 2 1 1 2 1 3 1 4 1 5 1 7 11 12 13 4 1 1 2 z 11 0 z 11 1 1 2 2 1 3 1 4 3 6 2 8 10 11 12 1 1 1 2 z 12 0 z 12 1 1 1 2 1 3 2 5 2 6 1 7 1 z 13 0 z 13 3 1 3 2 3 3 1 7 1 8 1 9 10 1 2 z 14 0 z 14 1 1 1 2 2 3 1 5 3 7 2 9 11 12 13 1 1 2 1 z 15 0 z 15 1 1 2 3 1 5 1 6 2 7 1 8 2 8 1 z 11 0 0 0 1 1 1 1 0 9 11 12 13 1 1 1 2 9 10 11 2 2 1 z 12 0 0 0 1 0 0 0 0 1 z 13 1 1 1 0 0 0 0 0 z 71 1 1 1 0 0 1 1 1 z 72 0 0 0 1 1 0 0 0 zd 1 0 0 0 0 0 1 1 1 zd 2 1 1 1 1 1 0 0 0 x y 1 1 3 1 2 2 3 3 5 2 9 3 15 1 14 2 15 3 13 4 10 9 11 1111 7 8 We choose zd=z 13 next (Should have been first? Since it's Value. Array is shortest? ) Note, z 8, z 9, za projection lines will be nearly coincident with that of z 7. xy 1 2 3 4 5 6 7 8 9 a b c d e f 1 2 3 4 5 6 7 8 9 a b 1 3 2 4 gap: 3 -7 yo(x-M)/|x-M| Value Arrays yo(x-M)/|x-M| Count Arrays 5 f 6 M d b c e a 8 7 9 x z 1 z 1 z 1 z 1 y z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 z 10 z 11 z 12 z 13 z 14 z 15 9 5 F 14 12 12 11 10 6 1 2 0 2 2 1 2 0 5 Mean

Cluster by splitting at gaps > 2 yo(x-M)/|x-M| Value Arrays yo(x-M)/|x-M| Count Arrays z 1 0 2 1 2 2 4 5 1 6 10 11 12 14 1 1 1 2 1 z 2 0 2 1 2 2 4 5 1 6 10 11 12 14 1 1 1 2 1 z 3 0 1 1 5 2 2 5 1 6 10 11 12 14 1 1 1 2 1 z 4 0 2 1 4 3 2 6 10 11 12 14 2 1 1 2 1 z 5 0 2 1 2 2 3 3 1 5 1 6 10 11 12 14 1 1 1 2 1 z 6 0 2 1 1 2 1 3 1 7 1 8 3 9 10 3 3 z 7 0 1 1 4 2 1 3 3 4 1 6 1 9 11 12 1 z 8 0 1 1 2 2 3 3 1 4 3 6 1 9 11 12 1 z 9 0 2 1 1 2 1 3 2 4 1 6 3 7 10 12 13 1 1 2 1 z 10 0 z 10 2 1 1 2 1 3 1 4 1 5 1 7 11 12 13 4 1 1 2 z 11 0 z 11 1 1 2 2 1 3 1 4 3 6 2 8 10 11 12 1 1 1 2 z 12 0 z 12 1 1 1 2 1 3 2 5 2 6 1 7 1 z 13 0 z 13 3 1 3 2 3 3 1 7 1 8 1 9 10 1 2 z 14 0 z 14 1 1 1 2 2 3 1 5 3 7 2 9 11 12 13 1 1 2 1 z 15 0 z 15 1 1 2 3 1 5 1 6 2 7 1 8 2 8 1 z 11 0 0 0 1 1 1 1 0 9 11 12 13 1 1 1 2 9 10 11 2 2 1 z 12 0 0 0 1 0 0 0 0 1 z 13 1 1 1 0 0 0 0 0 z 71 1 1 1 0 0 1 1 1 z 72 0 0 0 1 1 0 0 0 zd 1 0 0 0 0 0 1 1 1 zd 2 1 1 1 1 1 0 0 0 x y 1 1 3 1 2 2 3 3 5 2 9 3 15 1 14 2 15 3 13 4 10 9 11 1111 7 8 xy 1 2 3 4 5 6 7 8 9 a b c d e f 1 2 3 4 5 6 7 8 9 a b 1 3 2 4 5 f 6 M d b x z 1 z 1 z 1 z 1 y z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 z 10 z 11 z 12 z 13 z 14 z 15 9 5 F 14 12 12 11 10 6 1 2 0 2 2 1 2 0 5 Mean c e a 8 7 9 AND each red with each blue with each green, to get the subcluster masks (12 ANDs producing 5 sub-clusters.

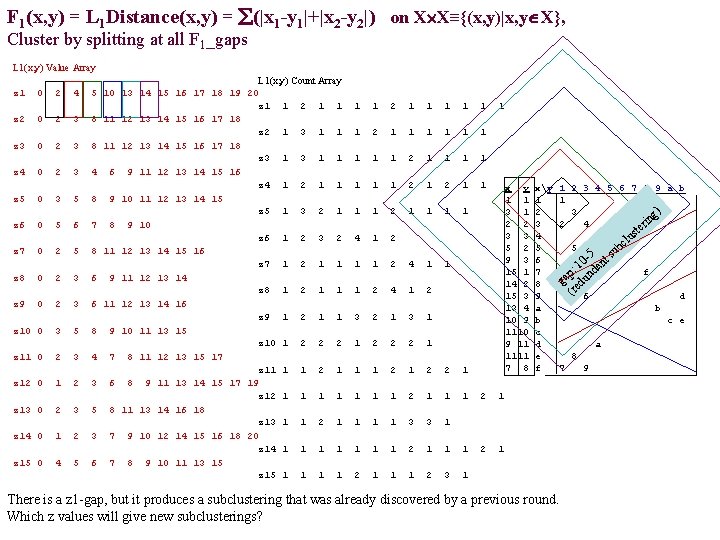
F 1(x, y) = L 1 Distance(x, y) = (|x 1 -y 1|+|x 2 -y 2|) on X X≡{(x, y)|x, y X}, Cluster by splitting at all F 1_gaps L 1(x, y) Value Array z 1 0 2 4 z 2 0 2 3 z 3 0 2 3 z 4 0 2 3 z 5 0 3 5 z 6 0 5 6 z 7 0 2 5 z 8 0 2 3 z 9 0 2 3 z 10 0 3 5 z 11 0 2 3 z 12 0 1 2 z 13 0 2 3 z 14 0 1 2 z 15 0 4 5 L 1(x, y) Count Array 5 10 13 14 15 16 17 18 19 20 z 1 1 2 1 1 8 11 12 13 14 15 16 17 18 z 2 1 3 1 1 8 11 12 13 14 15 16 17 18 z 3 1 1 4 6 9 11 12 13 14 15 16 z 4 1 2 1 1 8 9 10 11 12 13 14 15 z 5 1 3 2 1 7 8 9 10 z 6 1 2 3 2 8 11 12 13 14 15 16 z 7 1 2 1 1 6 9 11 12 13 14 z 8 1 2 1 1 6 11 12 13 14 16 z 9 1 2 1 1 8 9 10 11 13 15 z 10 1 2 2 2 4 7 8 11 12 13 15 17 z 11 1 1 2 1 3 6 8 9 11 13 14 15 17 19 z 12 1 1 5 8 11 13 14 16 18 z 13 1 1 2 1 3 7 9 10 12 14 15 16 18 20 z 14 1 1 6 7 8 9 10 11 13 15 z 15 1 1 1 2 1 1 1 1 1 2 1 1 2 1 1 4 1 2 1 1 2 4 1 2 3 2 1 3 1 1 2 2 2 1 1 x y 1 1 3 1 2 2 3 3 5 2 9 3 15 1 14 2 15 3 13 4 10 9 11 1111 7 8 1 1 1 2 2 1 1 1 1 3 3 1 1 2 1 1 1 2 3 1 xy 1 2 3 4 5 6 7 8 9 a b c d e f There is a z 1 -gap, but it produces a subclustering that was already discovered by a previous round. Which z values will give new subclusterings? 1 2 3 4 5 6 7 8 9 a b 1 3 g) in 2 4 r e st lu bc 5 -5 nt su 0 1 a p: und a g ed (r f 6 d b c e a 8 7 9

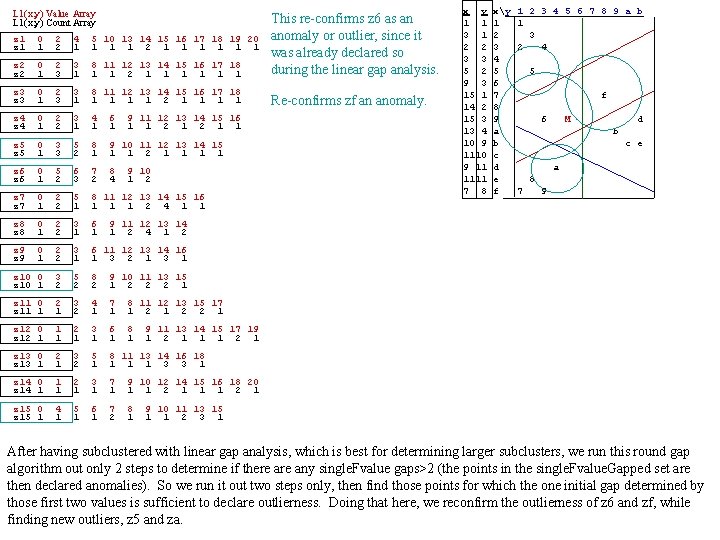
L 1(x, y) Value Array L 1(x, y) Count Array z 1 0 1 2 2 4 1 5 10 13 14 15 16 17 18 19 20 1 1 1 2 1 1 1 z 2 0 1 2 3 3 1 8 11 12 13 14 15 16 17 18 1 1 2 1 1 1 This re-confirms z 6 as an anomaly or outlier, since it was already declared so during the linear gap analysis. z 3 0 1 2 3 3 1 8 11 12 13 14 15 16 17 18 1 1 2 1 1 Re-confirms zf an anomaly. z 4 0 1 2 2 3 1 4 1 6 1 z 5 0 1 3 3 5 2 8 1 9 10 11 12 13 14 15 1 1 2 1 1 z 6 0 1 5 2 6 3 7 2 8 4 z 7 0 1 2 2 5 1 8 11 12 13 14 15 16 1 1 1 2 4 1 1 z 8 0 1 2 2 3 1 6 1 z 9 0 1 2 2 3 1 6 11 12 13 14 16 1 3 2 1 3 1 z 10 0 z 10 1 3 2 5 2 8 2 9 10 11 13 15 1 2 2 2 1 z 11 0 z 11 1 2 1 3 2 4 1 7 1 8 11 12 13 15 17 1 2 2 1 z 12 0 z 12 1 1 1 2 1 3 1 6 1 8 1 z 13 0 z 13 1 2 1 3 2 5 1 8 11 13 14 16 18 1 1 1 3 3 1 z 14 0 z 14 1 1 1 2 1 3 1 7 1 9 10 12 14 15 16 18 20 1 1 2 1 z 15 0 z 15 1 4 1 5 1 6 1 7 2 8 1 9 11 12 13 14 15 16 1 1 2 1 1 9 10 1 2 x y 1 1 3 1 2 2 3 3 5 2 9 3 15 1 14 2 15 3 13 4 10 9 11 1111 7 8 xy 1 2 3 4 5 6 7 8 9 a b c d e f 1 2 3 4 5 6 7 8 9 a b 1 3 2 4 5 f 6 M d b c e a 8 7 9 9 11 12 13 14 1 2 9 11 13 14 15 17 19 1 2 1 1 1 2 1 9 10 11 13 15 1 1 2 3 1 After having subclustered with linear gap analysis, which is best for determining larger subclusters, we run this round gap algorithm out only 2 steps to determine if there any single. Fvalue gaps>2 (the points in the single. Fvalue. Gapped set are then declared anomalies). So we run it out two steps only, then find those points for which the one initial gap determined by those first two values is sufficient to declare outlierness. Doing that here, we reconfirm the outlierness of z 6 and zf, while finding new outliers, z 5 and za.

yo(s 1 -M)/|s 1 -M|-69) Val Ct 0 1 3 1 4 2 7 1 8 1 9 2 10 1 12 4 14 5 15 2 16 4 17 1 18 4 19 5 20 1 21 2 22 2 23 8 24 4 25 3 26 2 27 5 28 3 29 4 30 4 31 3 32 2 33 2 34 4 35 5 36 2 37 2 38 1 39 1 40 1 41 1 43 1 44 1 45 1 52 1 60 3 61 4 62 3 63 10 64 15 65 9 66 3 67 1 69 2 F(i 39)=52 virginica 39 is an outlier. 2 clusters, F<52 (ct=99) and F>52 (50 Setosa) For virginica 1 Val Ct 0 1 1 1 2 2 3 5 4 6 5 11 6 12 7 4 8 2 9 5 10 1 17 1 22 1 24 2 25 1 27 1 28 1 29 2 30 1 31 3 32 4 33 1 34 4 35 2 36 2 37 4 38 4 39 5 40 4 42 6 43 2 44 7 45 5 47 2 48 3 49 3 50 3 51 4 52 3 53 2 54 2 55 4 56 2 57 1 58 1 59 1 60 1 61 1 62 1 63 1 64 1 66 1 F(i 39)=17 F<17 (50 Setosa) vers 1 Val Ct 0 1 2 4 3 1 4 1 5 3 6 3 7 8 8 3 9 7 10 6 11 4 12 4 13 3 15 2 19 2 20 2 21 1 26 2 27 3 28 4 30 2 31 5 32 4 33 3 34 1 36 3 37 5 38 4 39 5 40 7 41 4 42 2 43 2 44 1 45 6 46 4 47 5 48 1 49 2 50 5 51 1 52 2 54 2 55 1 57 2 58 1 60 1 62 1 63 1 64 1 65 2 Using F=yo(x-M)/|x-M|-MIN on IRIS, one stride at a time (s 1=setosa 1 first) F<19 (50 setosa) 19<F<22 {vers 8, 12, 39, 44, 49} 22<F virgini 39 Val Ct 0 1 1 2 2 1 4 2 6 1 7 1 8 7 9 2 10 2 11 7 12 2 13 3 14 7 15 4 16 10 17 4 18 6 19 9 20 3 21 6 22 3 23 6 24 3 25 1 27 3 28 2 32 1 39 1 40 1 41 1 42 8 43 13 44 17 45 4 46 5 47 1 F=32 vers 49 outlier. 32<F (50 Setosa, vir 39) AVG(ver 8, 12, 39, 44, 49) Val Ct 0 1 1 1 7 5 10 3 12 2 13 2 14 3 15 5 16 2 17 5 18 8 19 4 20 3 21 4 22 3 23 8 24 4 25 4 26 3 27 7 28 7 29 4 30 5 31 4 32 5 33 8 34 2 35 6 36 5 37 3 38 2 39 8 40 6 41 3 43 1 44 2 45 1 47 1 F=0 vir 32 outlier F=1 vir 18 outlier F=7 vir 6, 10, 19, 23, 36 subcluster?

For s 1 (i. e. , yo(s 1 -M)/|s 1 -M|-69) Val Ct 0 1 3 1 4 2 7 1 8 1 9 2 10 1 12 4 14 5 15 2 16 4 17 1 18 4 19 5 20 1 21 2 22 2 23 8 24 4 25 3 26 2 27 5 28 3 29 4 30 4 31 3 32 2 33 2 34 4 35 5 36 2 37 2 38 1 39 1 40 1 41 1 43 1 44 1 45 1 52 1 outlier 60 3 61 4 62 3 63 10 64 15 65 9 66 3 67 1 69 2 F(i 39)=52 i 39=virgi 39 outlier. Clusters, F<52 (ct=99) and F>52 (50 Setosa) On Clus(F<52) ver 1 F(virg 7)=0 outlier F(virg 32)=25 outlier Val Ct 0 1 4 1 5 5 6 3 7 5 8 3 9 8 10 11 11 14 12 8 13 8 14 5 15 3 16 7 17 5 18 6 19 2 20 1 21 1 22 1 25 1 On remaining vir 1 Val Ct 0 1 0 1 1 2 2 1 4 1 5 1 6 2 7 2 8 2 9 4 10 1 11 4 12 3 13 4 14 2 15 6 16 4 17 6 19 4 20 5 21 5 22 2 23 1 24 2 25 5 26 4 27 4 28 1 29 2 30 6 31 2 32 1 33 1 34 1 35 2 36 1 38 1 39 1 F=yo(x-M)/|x-M|-MIN on IRIS, subclustering as we go. On Remaining, mx mn mx mx Val Ct 0 3 1 4 2 11 3 14 4 14 e 38 e 19 i 20 F 5 9 0 9 9 11 9 6 10 e 4 9 0 3 7 9 7 2 e 38 e 19 9 3 0 5 11 outlier 8 6 i 20 11 7 5 0 11 outlier 9 2 11 2 On Remaining, mn mx mx mx Val Ct 0 1 2 1 On Remaining w e 35 3 4 Val Ct 4 3 0 1 i 26 outlier 5 5 3 2 6 4 7 5 8 7 9 8 10 3 11 5 12 2 13 4 14 5 15 7 16 5 e 35 e 10 17 4 18 1 e 35 0 7 20 1 e 10 7 0 outlier i 30 i 31 i 26 i 8 i 36 5 5 4 5 7 0 5 3 6 9 outlier 5 0 5 3 5 outlier 3 5 0 4 7 outlier 6 3 4 0 7 outlier 9 5 7 7 0 outlier On Remaining, max's Val Ct 0 2 e 8 outlier 1 2 e 11 outlier 7 2 On Remaining, max's Val Ct 8 1 0 2 e 44 outlier 9 4 6 1 On Remaining, 10 1 7 2 mx mx mx mn 11 2 8 1 Val Ct On Remaining, 12 2 9 3 0 1 mn mn mx mx 13 4 10 1 1 2 Val Ct 14 3 11 3 2 3 0 1 12 5 15 1 3 13 2 5 5 16 4 2 3 14 2 6 4 17 2 3 7 15 3 7 5 4 7 18 2 17 3 8 2 5 7 19 3 18 3 9 3 6 5 20 4 19 5 10 5 7 5 21 6 20 1 11 4 8 3 21 9 22 5 12 7 9 8 22 5 13 5 23 5 10 4 23 4 14 2 24 4 11 4 24 2 15 4 12 11 25 2 26 4 13 4 26 2 27 2 17 7 14 8 27 1 28 2 18 4 15 4 28 2 29 4 16 1 30 2 29 4 20 2 18 1 31 3 i 44 i 3 21 2 30 5 32 3 i 44 0 4 22 1 31 1 33 2 0 i 3 4 0 24 1 i 3 32 3 34 3 ^^outlier 25 1 i 30 5 33 2 35 2 27 2 i 31 5 34 2 36 1 i 26 4 35 3 37 1 5 29 2 i 8 38 1 i 36 7 36 2 39 1 Rem mn mx 37 1 42 1 e 36 Val Ct 38 1 outlier? 0 1 39 1 i 8 1 1 41 2 i 10 i 36 2 1 44 2 i 6 i 23 3 1 46 1 i 19 On Remaining, mn mx mx mx 4 1 48 1 i 18 e 13 e 30 e 32 Val Ct 5 1 0 1 e 13 0 7 3 outlier 6 1 1 1 e 30 7 0 6 outlier 8 1 i 6 i 8 i 10 i 19 i 23 i 35 2 1 e 32 3 6 0 9 3 i 6 0 5 10 5 3 20 3 5 10 5 i 8 5 0 10 9 6 15 4 6 11 5 i 10 10 10 0 14 12 19 5 5 12 3 i 19 5 9 14 0 4 22 6 4 13 7 i 23 3 6 12 4 0 20 7 9 14 6 8 4 15 4 i 35 20 15 19 22 20 0 9 4 16 6 10 4 17 7 i 6 i 10 i 18 i 19 i 23 i 35 11 3 18 5 all declared outliers 12 5 19 4 13 6 20 2 i 44 i 45 i 49 i 5 i 37 i 1 14 6 21 3 4 6 6 15 7 i 44 0 3 8 22 7 5 4 5 16 5 i 45 3 0 6 23 4 6 2 6 17 4 i 49 8 6 0 24 3 i 5 4 5 6 0 5 5 18 4 25 1 5 0 4 not outlier 20 1 i 37 6 4 2 26 1 6 5 4 0 outlier 22 1 i 1 27 2

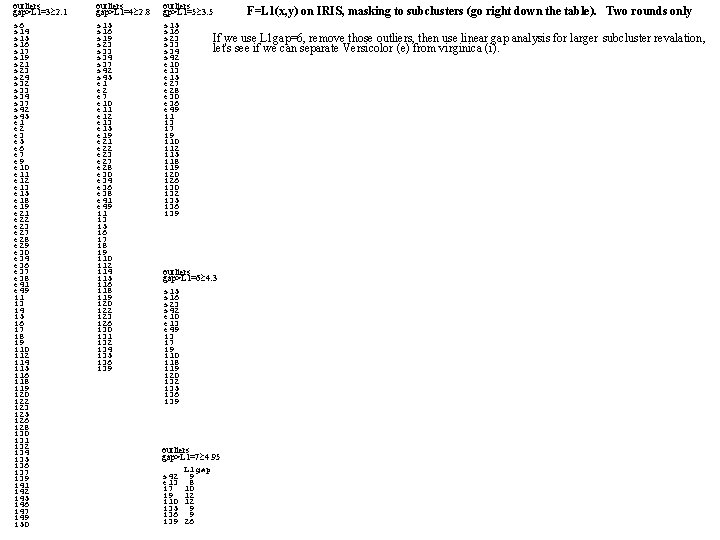
outliers gap>L 1=3 2. 1 s 6 s 14 s 15 s 16 s 17 s 19 s 21 s 23 s 24 s 32 s 33 s 34 s 37 s 42 s 45 e 1 e 2 e 3 e 5 e 6 e 7 e 9 e 10 e 11 e 12 e 13 e 15 e 18 e 19 e 21 e 22 e 23 e 27 e 28 e 29 e 30 e 34 e 36 e 37 e 38 e 41 e 49 i 1 i 3 i 4 i 5 i 6 i 7 i 8 i 9 i 10 i 12 i 14 i 15 i 16 i 18 i 19 i 20 i 22 i 23 i 25 i 26 i 28 i 30 i 31 i 32 i 34 i 35 i 36 i 37 i 39 i 41 i 42 i 45 i 46 i 47 i 49 i 50 outliers gap>L 1=4 2. 8 s 15 s 16 s 19 s 23 s 34 s 37 s 42 s 45 e 1 e 2 e 7 e 10 e 11 e 12 e 13 e 15 e 19 e 21 e 22 e 23 e 27 e 28 e 30 e 34 e 36 e 38 e 41 e 49 i 1 i 3 i 5 i 6 i 7 i 8 i 9 i 10 i 12 i 14 i 15 i 16 i 18 i 19 i 20 i 22 i 23 i 26 i 30 i 31 i 32 i 34 i 35 i 36 i 39 outliers F=L 1(x, y) on IRIS, masking to subclusters (go right down the table). gp>L 1=5 3. 5 s 16 s 23 If we use L 1 gap=6, remove those outliers, then use linear gap analysis for larger s 33 let's see if we can separate Versicolor (e) from virginica (i). s 34 s 42 e 10 e 13 e 15 e 27 e 28 e 30 e 36 e 49 i 1 i 3 i 7 i 9 i 10 i 12 i 15 i 18 i 19 i 20 i 26 i 30 i 32 i 35 i 36 i 39 outliers gap>L 1=6 4. 3 s 15 s 16 s 23 s 42 e 10 e 13 e 49 i 3 i 7 i 9 i 10 i 18 i 19 i 20 i 32 i 35 i 36 i 39 outliers gap>L 1=7 4. 95 L 1 gap s 42 9 e 13 8 i 7 10 i 9 12 i 10 12 i 35 9 i 36 9 i 39 26 Two rounds only subcluster revalation,

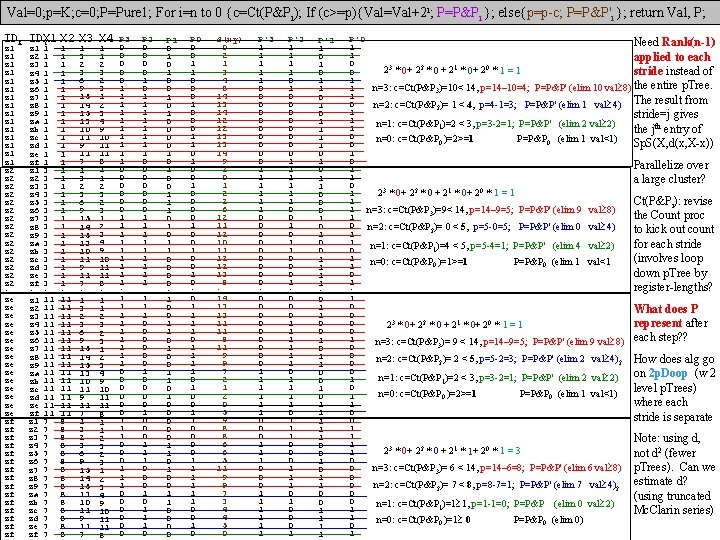
Val=0; p=K; c=0; P=Pure 1; For i=n to 0 {c=Ct(P&Pi); If (c>=p){Val=Val+2 i; P=P&Pi }; else{p=p-c; P=P&P'i }; return Val, P; IDX IDYX 1 X 2 X 3 X 4 z 1 z 1 z 1 z 1 z 2 z 2 z 2 z 2 : ze ze ze ze zf zf zf zf z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf : z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf 1 1 1 1 3 3 3 3 : 11 11 11 11 7 7 7 7 1 1 1 1 1 1 1 1 : 11 11 11 11 8 8 8 8 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 : 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 : 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 P 3 0 0 0 1 1 1 1 1 : 1 1 1 1 1 0 0 0 0 0 0 P 2 0 0 1 0 1 1 1 1 0 0 0 0 1 1 1 0 0 0 1 0 0 0 1 1 1 0 P 1 0 1 0 0 1 1 1 0 0 : 1 0 0 1 1 0 1 0 0 0 1 1 0 0 P 0 0 0 1 1 0 0 1 0 0 1 0 : 0 1 1 1 1 0 1 0 0 1 1 1 0 0 1 0 d(xy) 0 2 1 3 4 8 14 13 14 12 12 13 13 14 9 2 0 1 2 2 6 12 11 12 10 11 12 12 13 8 : 14 13 13 11 11 8 11 9 9 7 2 1 2 0 5 9 8 8 6 6 5 11 9 9 7 3 4 4 5 0 P'3 1 1 1 0 0 0 0 0 : 0 0 0 0 0 1 1 1 1 1 1 P'2 1 1 0 1 0 0 0 0 1 1 1 0 0 0 1 : 0 0 0 1 1 1 0 1 1 1 0 0 0 1 P'1 1 0 1 0 1 1 0 0 0 1 1 : 0 1 1 0 0 1 0 1 1 1 0 0 1 1 P'0 Need Rank(n-1) 1 1 applied to each 0 23 * 0+ 22 * 0 + 21 * 0+ 20 * 1 = 1 0 stride instead of 1 n=3: c=Ct(P&P 3)=10< 14, p=14– 10=4; P=P&P' (elim 10 val 8) the entire p. Tree. 1 1 0 n=2: c=Ct(P&P 2)= 1 < 4, p=4 -1=3; P=P&P' (elim 1 val 4) The result from 1 stride=j gives 1 n=1: c=Ct(P&P 1)=2 < 3, p=3 -2=1; P=P&P' (elim 2 val 2) 1 the jth entry of 0 n=0: c=Ct(P&P 0 )=2>=1 P=P&P 0 (elim 1 val<1) Sp. S(X, d(x, X-x)) 0 1 0 Parallelize over 1 1 a large cluster? 0 3 * + 22 * 1 * + 20 * 2 + 2 1 0 0 1=1 0 1 Ct(P&Pi): revise 1 n=3: c=Ct(P&P 3)=9< 14, p=14– 9=5; P=P&P' (elim 9 val 8) the Count proc 1 0 n=2: c=Ct(P&P 2)= 0 < 5, p=5 -0=5; P=P&P' (elim 0 val 4) to kick out count 1 1 for each stride n=1: c=Ct(P&P 1)=4 < 5, p=5 -4=1; P=P&P' (elim 4 val 2) 0 1 (involves loop n=0: c=Ct(P&P 0 )=1>=1 P=P&P 0 (elim 1 val<1 1 down p. Tree by 0 1 register-lengths? : 1 0 What does P 0 0 represent after 23 * 0+ 22 * 0 + 21 * 0+ 20 * 1 = 1 0 1 n=3: c=Ct(P&P 3)= 9 < 14, p=14– 9=5; P=P&P' (elim 9 val 8) each step? ? 0 0 n=2: c=Ct(P&P 2)= 2 < 5, p=5 -2=3; P=P&P' (elim 2 val 4)2 How does alg go 0 0 on 2 p. Doop (w 2 n=1: c=Ct(P&P 1)=2 < 3, p=3 -2=1; P=P&P' (elim 2 val 2) 1 0 level p. Trees) n=0: c=Ct(P&P 0 )=2>=1 P=P&P 0 (elim 1 val<1) 1 where each 1 0 stride is separate 0 1 1 Note: using d, 1 23 * 0+ 22 * 0 + 21 * 1+ 20 * 1 = 3 1 not d 2 (fewer 0 n=3: c=Ct(P&P 3)= 6 < 14, p=14– 6=8; P=P&P' (elim 6 val 8) p. Trees). Can we 0 0 0 n=2: c=Ct(P&P 2)= 7 < 8, p=8 -7=1; P=P&P' (elim 7 val 4)2 estimate d? 0 (using truncated 0 n=1: c=Ct(P&P 1)=1 1, p=1 -1=0; P=P&P (elim 0 val 2) 1 Mc. Clarin series) 1 n=0: c=Ct(P&P 0 )=1 0 P=P&P 0 (elim 0) 0 1

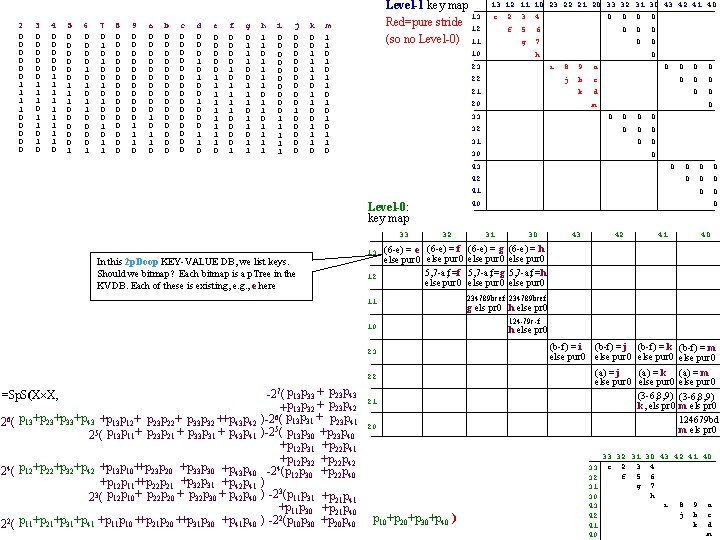
2 0 0 0 1 1 0 0 0 3 0 0 0 1 1 1 0 1 0 4 0 0 0 1 1 1 1 1 0 5 0 0 0 1 1 1 0 0 0 1 6 0 0 1 0 1 1 0 0 1 7 0 1 0 1 0 0 1 1 8 0 0 0 0 9 0 0 0 1 1 1 0 a 0 0 0 0 0 1 0 1 1 0 b 0 0 0 0 c 0 0 0 0 d 0 0 0 1 0 0 0 1 1 0 e 0 0 0 1 1 1 1 1 0 f 0 0 1 0 1 1 0 0 1 g 0 1 1 1 0 1 1 h 1 1 0 1 1 i 0 0 0 0 0 1 1 1 j 0 0 0 0 0 1 0 0 0 k 0 0 1 1 0 0 1 1 1 0 Level-1 key map 13 Red=pure stride 12 (so no Level-0) 11 m 1 1 0 1 0 1 0 13 12 11 10 23 22 21 20 33 32 31 30 43 42 41 40 e 10 2 3 4 f 5 6 g 7 0 0 0 0 0 h 23 0 i 22 21 8 9 a j b c k d 20 0 32 0 0 0 0 31 30 0 41 32 (6 -e) = e (6 -e) = f else pur 0 5, 7 -a, f=f else pur 0 11 10 23 22 =Sp. S(X X, 26( p 13+p 23+p 33+p 43 +p 13 p 12+ p 23 p 22+ p 33 p 32 ++p 43 p 42 25( p 13 p 11+ p 23 p 21 + p 33 p 31 + p 43 p 41 24( p 12+p 22+p 32+p 42 +p 13 p 10++p 23 p 20 +p 33 p 30 +p 43 p 40 +p 12 p 11++p 22 p 21 +p 32 p 31 +p 42 p 41 3 2 ( p 12 p 10+ p 22 p 20 + p 32 p 30 + p 42 p 40 22( p 11+p 21+p 31+p 41 +p 11 p 10 ++p 21 p 20 ++p 31 p 30 +p 41 p 40 -27( p 13 p 33 + p 23 p 43 +p 13 p 32 + p 23 p 42 6 ) -2 ( p 13 p 31 + p 23 p 41 ) -25( p 13 p 30 +p 23 p 40 +p 12 p 31 +p 22 p 41 +p 12 p 32 +p 22 p 42 -24(p 12 p 30 +p 22 p 40 ) ) -23(p 11 p 31 +p 21 p 41 +p 11 p 30 +p 21 p 40 ) -22(p 10 p 30 +p 20 p 40 0 0 0 0 40 Level-0: key map 12 0 0 0 42 13 0 0 43 In this 2 p. Doop KEY-VALUE DB, we list keys. Should we bitmap? Each bitmap is a p. Tree in the KVDB. Each of these is existing, e. g. , e here 0 0 m 33 33 0 21 0 31 (6 -e) = g else pur 0 5, 7 -a, f=g else pur 0 30 43 42 40 (6 -e) = h else pur 0 5, 7 -a, f=h else pur 0 234789 bcef g els pr 0 h else pr 0 124 -79 c-f h else pr 0 (b-f) = i (b-f) = j (b-f) = k (b-f) = m else pur 0 (a) = j (a) = k else pur 0 (3 -6, 8, 9) k, els pr 0 20 p 10+p 20+p 30+p 40 ) 41 33 32 31 30 43 42 41 40 (a) = m else pur 0 (3 -6, 8, 9) m els pr 0 124679 bd m els pr 0 33 32 31 30 43 42 41 40 e 2 3 4 f 5 6 g 7 h i 8 9 a j b c k d m