SingleSource Shortest Paths Camino ms corto desdehacia una

Single-Source Shortest Paths “Camino más corto desde/hacia una fuente” Agustín J. González ELO 320: Estructura de Datos y Algoritmos 1

Introducción n n Un estudiante quiere buscar el camino más corto que le permita llegar desde su casa, a la de la polola (pololo) pasando sólo por avenidas (para hacerlo doble sentido). Un computador debe determinar la ruta más conveniente para un paquete hacia su destino. Se trata entonces de buscar la ruta más “económica” para ir desde un nodo a cada uno de los otros. Se trata de buscar las rutas de menor costo a cada uno de los nodos. El algoritmo breadth-first search obtiene la ruta más corta en grafos sin peso, en el cual cada arco se puede considerar de peso unitario. Variantes: Camino más corto a un destino único Camino más corto entre dos nodos cualquiera. 2

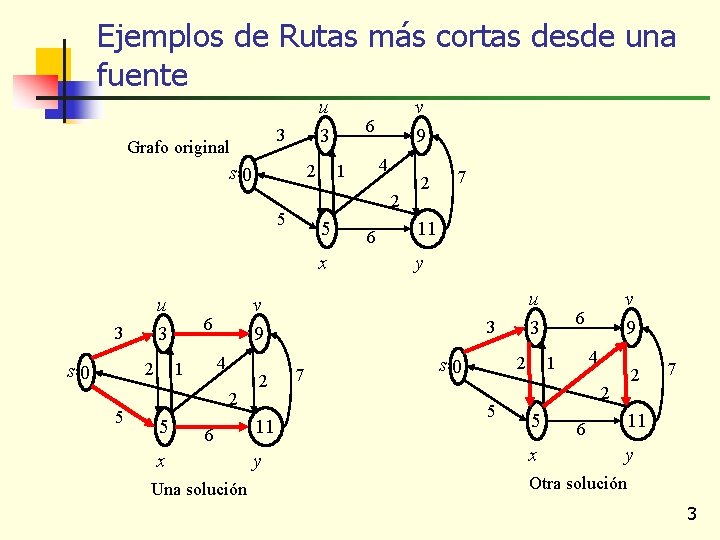
Ejemplos de Rutas más cortas desde una fuente u 3 3 Grafo original 2 s 0 2 5 s 0 5 4 2 5 6 2 7 11 y v 9 6 1 4 1 x 3 6 2 5 u 3 v 9 6 x Una solución 2 11 y u 3 3 7 2 s 0 5 v 9 6 4 1 2 2 5 x 7 11 6 y Otra solución 3

Observaciones n n Lema: Subcaminos del camino más corto son caminos más cortos. Dado un grafo dirigido con peso G=(V, E), sea p = <v 1, v 2, v 3, . . , vk> el camino más corto desde v 1 a vk, para 1 i j k sea pij = <vi, vi+1, , , vj> el subcamino de p desde el vértice vi al vj. Entonces pij es un camino más corto para ir de vi a vj. “Relajación” a través de un arco: Sea d[v] la estimación para la distancia más corta desde el nodo fuente. Al estudiar el arco (u, v) podemos mejorar la estimación dependiendo si la ruta vía u es mejor. Esta operación es conocida como “Relajar”. El algoritmo es: Relax (u, v, w){ if (d[v] > d[u] + w(u, v) ){ u v v d[v] = d[u] + w(u, v); u 2 2 5 6 p[v] = u; 5 9 } Relax(u, v) u 5 2 v 7 u 5 2 v 6 4

Algoritmo de Dijkstra(G, w, s) { for (cada vértice v en V[G] ) { d [v] = infinito; /* -”MAX_INT” por ejemplo*/ p [v] = NIL; } d [s] = 0; S = {}; /* S Contiene el arreglo de los nodos cuyo camino más corto ya ha sido encontrado */ Q = V [G]; while (Q != {}) { u = Extract_Min(Q); /* d [u] es Mínimo, lg V, |V| veces*/ S = S {u}; for ( cada vértice v en adj[u] ) /* un total de |E| veces */ Relax(u, v, w); /* O(lg V) */ } } 5

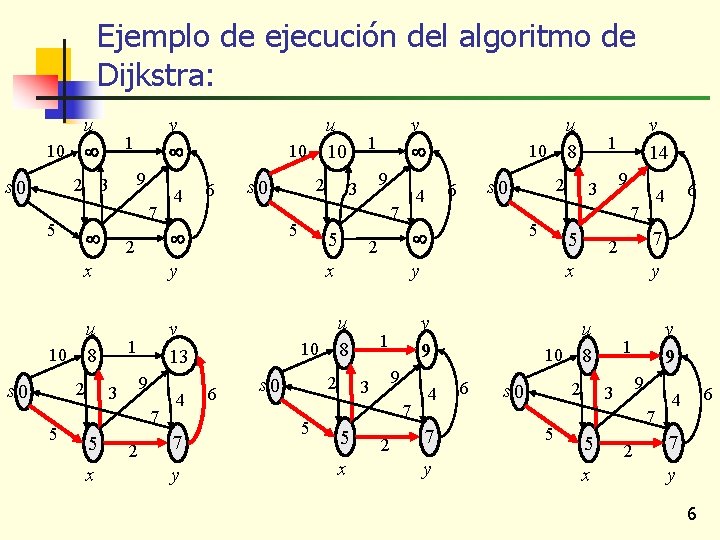
Ejemplo de ejecución del algoritmo de Dijkstra: u 10 1 9 2 3 s 0 7 5 2 5 9 7 x 2 4 7 y 1 9 3 5 6 2 5 9 3 7 5 x 2 9 3 4 7 y y u 10 8 6 2 s 0 5 6 4 7 2 x v 9 1 1 5 y u 10 8 v 14 7 5 2 2 s 0 6 4 x s 0 u 10 8 v 7 5 v 13 1 3 5 2 s 0 y u 10 8 s 0 4 6 x 2 u 10 10 v v 9 1 9 3 7 5 x 2 6 4 7 y 6

Comentarios sobre Algoritmo de Dijkstra n El tiempo de ejecución depende de la implementación de la cola de prioridad. Si se usara un arreglo lineal, Extract_Min toma O(V) con lo cual el algoritmo toma O(V 2 +E) = O(V 2). Si se usa un heap binario, Extract_Min toma O(lg V) con lo cual se reduce el tiempo total a =O(E lg V). Dijkstra(G, w, s) { for (cada vértice v en V[G] ) { d [v] = infinito; p [v] = NIL; } d [s] = 0; S = {}; /* S Contiene el arreglo de los nodos cuyo camino más corto ya ha sido encontrado */ Q = V [G]; while (Q != {}) { O(log|V|) cada vez, |V| veces u = Extract_Min(Q); S = S {u}; |E| veces for ( cada vértice v en adj[u] ) Relax(u, v, w); O(log |V|) } } Total=O(|V| log|V| +|E| log|V|) = O(|E| log |V|) O(|V|) 7

Comentarios sobre Algoritmo de Dijkstra n n Se supone que todos los arcos tienen peso no negativo. ¿Qué pasa si hay pesos negativos? Recordemos el supuesto del algoritmo: cuando extraemos un mínimo, la incorporación de nuevos nodos no mejorará su distancia a la fuente. -10 s S Si tenemos arcos negativos, entonces puede ocurrir que nodos por incorporar mejoren la situación de aquellos ya ingresados a S. Esta situación no es considerada en Dijkstra 8

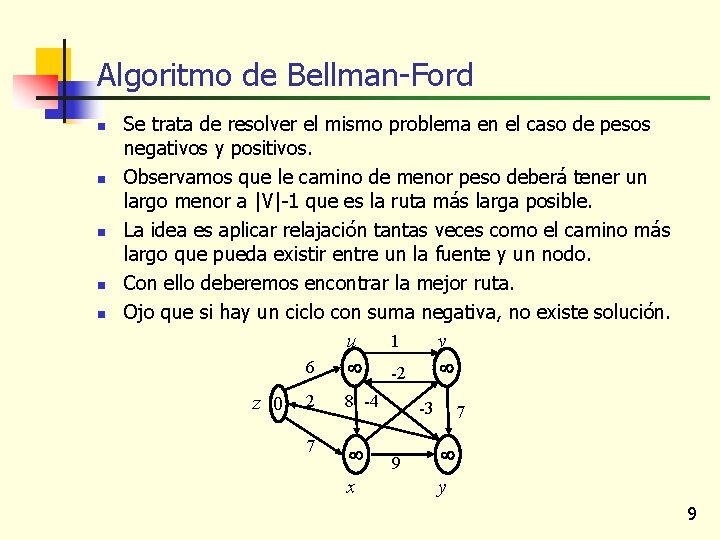
Algoritmo de Bellman-Ford n n n Se trata de resolver el mismo problema en el caso de pesos negativos y positivos. Observamos que le camino de menor peso deberá tener un largo menor a |V|-1 que es la ruta más larga posible. La idea es aplicar relajación tantas veces como el camino más largo que pueda existir entre un la fuente y un nodo. Con ello deberemos encontrar la mejor ruta. Ojo que si hay un ciclo con suma negativa, no existe solución. u v 1 6 -2 z 0 2 8 -4 7 x -3 9 7 y 9

Algoritmo de Bellman-Ford int Bellman-Ford(G, w, s) { for (cada vértice v en V[G] ) { d [v] = infinito; /* -”MAX_INT” por ejemplo*/ p [v] = NIL; } d [s] = 0; for (i=1 to |V [G]| -1 ) /* total de |V|-1 veces */ for (cada arco (u, v) en E[G] ) /*cada vez |E| veces */ Relax(u, v, w); for ( cada arco (u, v) en E[G] ) if(d [v] > d [u]+w(u, v)) return 0; /* False; no existe camino mínimo */ return 1; } 10

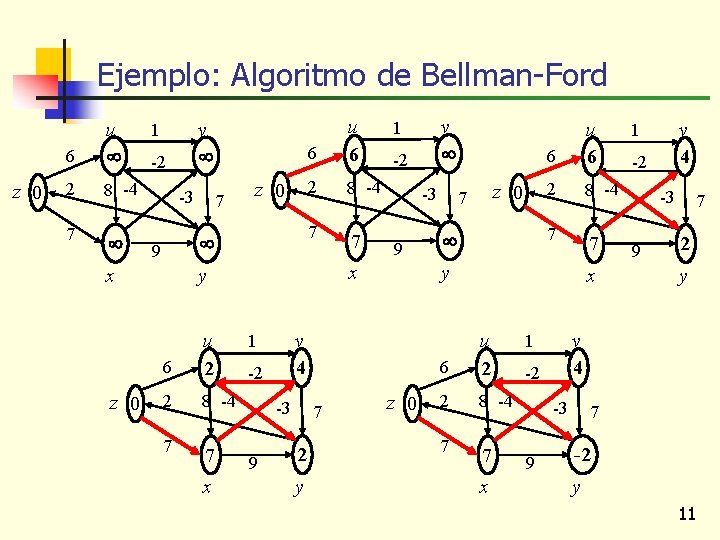
Ejemplo: Algoritmo de Bellman-Ford z 0 6 u 2 8 -4 7 -2 -3 7 z 0 9 x z 0 v 1 6 u 6 2 8 -4 7 7 6 u 2 2 8 -4 7 7 x -2 -3 9 x y -2 -3 9 7 2 y z 0 7 6 u 6 2 8 -4 7 7 y v 4 1 v 1 z 0 x 6 u 2 2 8 -4 7 7 x -2 -3 9 7 2 y v 4 1 -2 -3 9 v 4 1 7 -2 y 11

Algoritmo de Bellman-Ford int Bellman-Ford(G, w, s) { for (cada vértice v en V[G] ) { d [v] = infinito; p [v] = NIL; } d [s] = 0; for (i=1 to |V [G]| -1 ) for (cada arco (u, v) en E[G] ) Relax(u, v, w); } for ( cada arco (u, v) en E[G] ) if(d [v] > d [u]+w(u, v)) return 0; return 1; O(|V|) |V|-1 veces Cada vez |E| veces O(1) cada vez O(|E|) El tiempo de ejecución es O(|V|+ (|V|-1)*|E| + |E|) = O(|V||E|). 12