Relative Velocity 3 4 Relative Velocity Who is









- Slides: 10

Relative Velocity

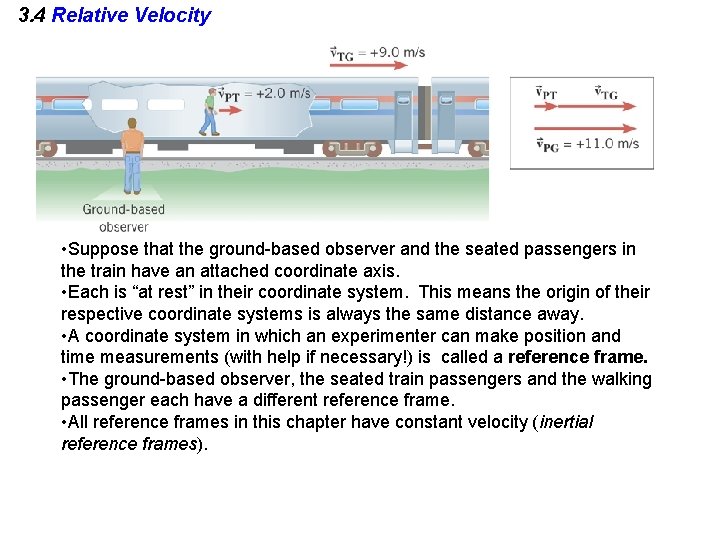
3. 4 Relative Velocity Who is “at rest” in this picture? Is it the ground-based observer? The seated passengers in the train? As the earth turns and the universe expands, one thing is certain: the idea of velocity is relative.

3. 4 Relative Velocity • Suppose that the ground-based observer and the seated passengers in the train have an attached coordinate axis. • Each is “at rest” in their coordinate system. This means the origin of their respective coordinate systems is always the same distance away. • A coordinate system in which an experimenter can make position and time measurements (with help if necessary!) is called a reference frame. • The ground-based observer, the seated train passengers and the walking passenger each have a different reference frame. • All reference frames in this chapter have constant velocity (inertial reference frames).

3. 4 Relative Velocity Consider the reference frame of the train (and its seated passengers). Let v. PT = velocity of the (moving) Passenger relative to the Train = +2. 0 m/s Consider the reference frame of the ground-based observer. Let VTG = velocity of the Train relative to the Ground = +9. 0 m/s Then what is the velocity of the Passenger relative to the Ground (VPG)?

Relative Velocity A person, standing on the ground, measures the velocity of a car to be VCG where: VCG = velocity of the Car relative to the Ground = +25 m/s. The driver of the car looks out the window and sees the ground go past her with a velocity of VGC, where: VGC = velocity of the Ground relative to the Car. How is VGC related to VCG? A. VGC = VCG = +25 m/s B. VGC = -VCG = -25 m/s C. VGC = 0 since the ground isn’t moving

A car and a bus A slower moving car is traveling behind a faster moving bus. In the reference frame of a ground based observer, the velocities of the two vehicles are: v. CG = velocity of the Car in the reference frame of the Ground = +15 m/s v. BG = velocity of the Bus in the reference frame of the Ground = +20 m/s. What is the velocity of the bus in the reference frame of the car? if the In other words, what is the velocity of the bus as measured by the driver of the car? A. +35 m/s B. +5 m/s C. -35 m/s D. -5 m/s

A car and a bus A slower moving car is traveling behind a faster moving bus. In the reference frame of a ground based observer, the velocities of the two vehicles are: v. CG = velocity of the Car in the reference frame of the Ground = +15 m/s. v. BG = velocity of the Bus in the reference frame of the Ground = +20 m/s. What is the velocity of the bus in the reference frame of the car? if the In other words, what is the velocity of the bus as measured by the driver of the car? VBC = VBG + VGC where VGC = - VCG = -15 m/s V BC = +20 m/s + - 15 m/s = +5 m/s

Up the down escalator The escalator that leads down into a subway station has a length of 30. 0 m and a speed of 1. 8 m/s relative to the ground. A student is coming out of the station by running in the wrong direction on this escalator. The local record time for this trick is 11 s. Relative to the escalator, what speed (magnitude only) must the student exceed in order to beat the record? If we follow the rule, our equation should be: VSE = VSG + VGE

Up the down escalator The escalator that leads down into a subway station has a length of 30. 0 m and a speed of 1. 8 m/s relative to the ground. A student is coming out of the station by running in the wrong direction on this escalator. The local record time for this trick is 11 s. VSE = VSG + VGE Knowns VEG = +1. 8 m/s: magnitude is given, sign is arbitrary VGE = - VEG = -1. 8 m/s VSG = - (30 m/11 s) = - 2. 7 m/s: relative to the groundbased observer, the student traveled 30 m in 11 s. Since he walked against the elevator, the sign is opposite to that of the elevator relative to the ground. Find: |VSE |, speed of the student relative to the elevator.

Up the down escalator The escalator that leads down into a subway station has a length of 30. 0 m and a speed of 1. 8 m/s relative to the ground. A student is coming out of the station by running in the wrong direction on this escalator. The local record time for this trick is 11 s. Relative to the escalator, what speed (magnitude only) must the student exceed in order to beat the record? VSE = VSG + VGE VSE = (-2. 7 + - 1. 8)m/s VSE = -4. 5 m/s speed is 4. 5 m/s
 Initial velocity and final velocity formula
Initial velocity and final velocity formula Darcy's law
Darcy's law Is v final velocity
Is v final velocity Rotational motion and the law of gravity
Rotational motion and the law of gravity Unit 2
Unit 2 Site:slidetodoc.com
Site:slidetodoc.com Angular acceleration formula with radius
Angular acceleration formula with radius Linear acceleration vs tangential acceleration
Linear acceleration vs tangential acceleration Instantaneous velocity vs average velocity
Instantaneous velocity vs average velocity Define relative velocity
Define relative velocity Relative triangles
Relative triangles



















