PreCalculus Daniela Calderon Erika Jaime Tapia Esther Duran

Pre-Calculus Daniela Calderon Erika Jaime Tapia Esther Duran Veronica Barragan Period 4

Functions and their Graphs • The Properties of Lines • a line has no beginning or end • parallel lines lie on the same plane and will extend forever without ever touching • perpendicular lines intersect and form 90 degree angles • intersecting lines are lines that will cross paths at some point • a transversal is a line that crosses a pair of parallel lines at a slant

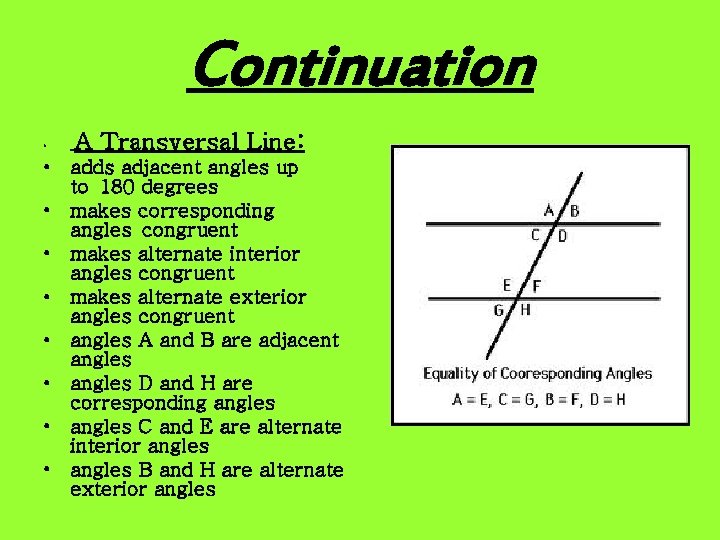
Continuation • A Transversal Line: • adds adjacent angles up to 180 degrees • makes corresponding angles congruent • makes alternate interior angles congruent • makes alternate exterior angles congruent • angles A and B are adjacent angles • angles D and H are corresponding angles • angles C and E are alternate interior angles • angles B and H are alternate exterior angles

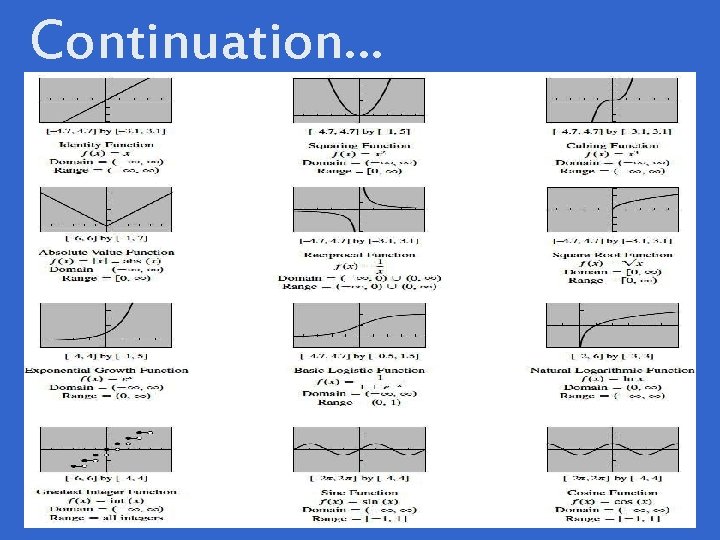
Twelve Basic Functions • • • The identity function has the equation f(x)= x. The graph falls left and rises right. This function has a domain and range of negative infinity to infinity and it is continuous. The graph looks like a diagonal line The squaring function has the equation f(x)= x^2. This graph rises on the left and right. It has a domain of negative infinity to infinity and a range of 0 to infinity. Its absolute minimum is at (0, 0) and is continuous. This graph looks like the letter "U" The cubing function has the equation f(x)= x^3. This graph falls to the left and rises to the right. This function has a domain and range of negative infinity to infinity and is continuous. The square root function has the eqation f(x)= x^(1/2). The graph has a domain and range of 0 to infinity and its absolute minimum is at (0, 0). This function is also continuous The natural logarithm function has the equation f(x)= ln x. It has a domain of 0 to infinity and a range of negative infinity to infinity. This function is continuous and it has a vertical asymptote x=0 The reciprocal function has the equation f(x)= 1/x. This function is not continuous and it has a vertical asymptote of x=0 and a horizontal asymptote of y=0. This function has a domain and range of (negative infinity to 0) u (0 to infinity)

MORE FUNCTIONS • • • The exponential function has the equation f(x)= e^x. This function has a domain of negative infinity to infinity and a range of 0 to infinity and is continuous. This function has a horizontal asymptote of y=0 The sine function has the equation f(x)= sinx. This function has a domain of negative infinity to infinity and a range of negative 1 to 1. This function is also periodic and continuous The cosine function has the equation f(x)= cosx. This function has a domain of negative infinity to infinity and a range of negative one to one. This function/graph is continuous and periodic but unlike sine, the cosine function does not start at (0, 0) The absolute value function has the equation f(x)= lxl. This function has a domain of negative infinity to infinity and a range of 0 to infinity. Its graph is continuous, has an absolute value minimum of (0, 0) and rises to the left and right in a "v" shape. The greatest integer function has an equation of f(x)= {x}. This function has a domain of negative infinity to infinity and all integers as its range. This graph is not continuous and has jump discontinuities at integer values of x The logistic function has an equation of f(x)= 1/1+e^ -x. This function has a domain of negative infinity to infinity and a range of 0 to one. The graph is continuous and has two horizontal asymptotes

Continuation…

Translations Horizontal translations • y= f(x-c) would equal a translation of the graph to the right c units • y= f(x+c) this would be a translation of the graph to the left c units

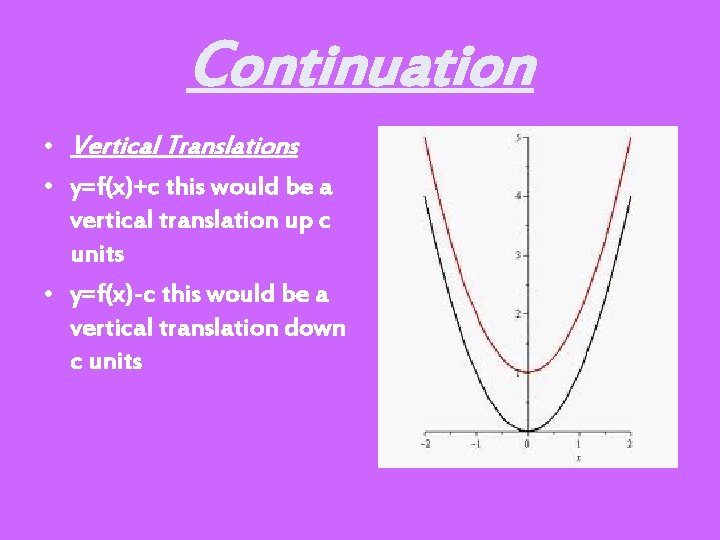
Continuation • Vertical Translations • y=f(x)+c this would be a vertical translation up c units • y=f(x)-c this would be a vertical translation down c units

Continuation… • Reflections • y= -f(x) is a reflection of the graph along the x-axis • y= f(-x) is a reflection of the graph along the y-axis

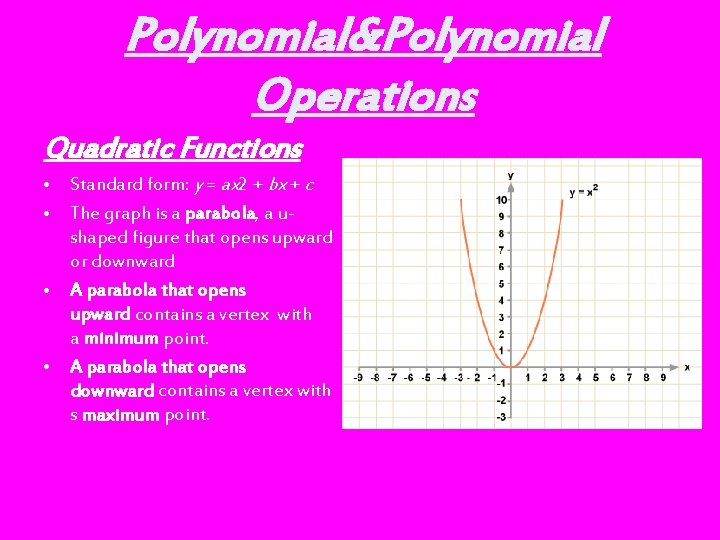
Polynomial&Polynomial Operations Quadratic Functions • Standard form: y = ax 2 + bx + c • The graph is a parabola, a ushaped figure that opens upward or downward • A parabola that opens upward contains a vertex with a minimum point. • A parabola that opens downward contains a vertex with s maximum point.

Continuation. . • The domain of a quadratic function is all real numbers. • The axis of symmetry divides the parabola into mirror images forming a vertical line. • The x-intercepts are the points at which a parabola intersects the x-axis. These points are also known as zeroes, roots, solutions, and solution sets. Each quadratic function has two, one, or no x-intercepts.

• • • Polynomial Functions Polynomial Function - A function that is defined by a polynomial; it is of the form f (x) = a n x n + a n-1 x n 1 +. . . + a 2 x 2 + a 1 x + a 0 , where a n, a n-1, …, a 1, a 0 are real numbers, n is a nonnegative integer and a n≠ 0. One-to-one functions: A function for which every element of the range of the function corresponds to exactly one element of the domain. y = f(x) is a function if it passes the vertical line test. It is a 1 -1 function if it passes both the vertical line test and the horizontal line test.

Synthetic Division • Synthetic Division: : A method of dividing polynomials when the divisor is a polynomial of the first degree, by using only the coefficients of the terms. • 1. Drop the first coefficient below the horizontal line. • 2. Multiply that number you drop by the number in the "box". Product is placed above the horizontal line just below the second coefficient. • 3. Add the column of numbers, then put the sum directly below the horizontal line. • 4. Repeat the process until you run out of columns to add.

Real Zeros Complex Numbers • Real zeros are the xintercepts of a function while the complex numbers are the imaginary solutions to the functions.

Rational Functions • A rational function is a function that can be written as the ratio of two polynomials. • A rational equation is an equation in which two rational expressions are set equal to each other. These expressions obey the same rules as fractions. The equations can be solved by cross-multiplying. Division by zero is undefined, so that a solution causing formal division by zero is rejected.

The Fundamental Theorem of Algebra • The fundamental theorem of algebra states that every polynomial equation over the field of complex numbers of degree higher than one has a complex solution. Polynomials of the form , with a, b, . . . coefficients real or complex, can be factored completely into where the r, s, . . . are complex numbers. The theorem also gives the number of solutions to the polynomial equation. If f(x) is a polynomial of degree n, then f(x) has exactly n roots, counting complex numbers and multiple roots.

Exponential and Logarithmic Functions

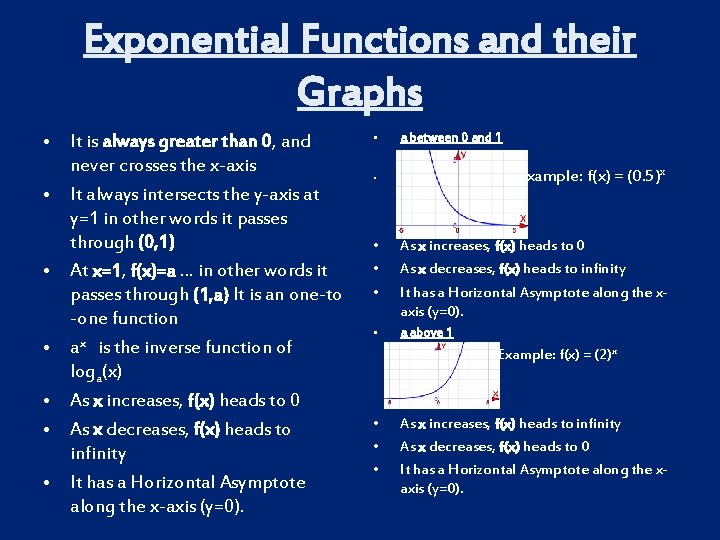
Exponential Functions and their Graphs • It is always greater than 0, and never crosses the x-axis • It always intersects the y-axis at y=1 in other words it passes through (0, 1) • At x=1, f(x)=a. . . in other words it passes through (1, a) It is an one-to -one function • ax is the inverse function of loga(x) • As x increases, f(x) heads to 0 • As x decreases, f(x) heads to infinity • It has a Horizontal Asymptote along the x-axis (y=0). • a between 0 and 1 Example: f(x) = (0. 5)x • • As x increases, f(x) heads to 0 As x decreases, f(x) heads to infinity It has a Horizontal Asymptote along the xaxis (y=0). • a above 1 Example: f(x) = (2)x • • • As x increases, f(x) heads to infinity As x decreases, f(x) heads to 0 It has a Horizontal Asymptote along the xaxis (y=0).

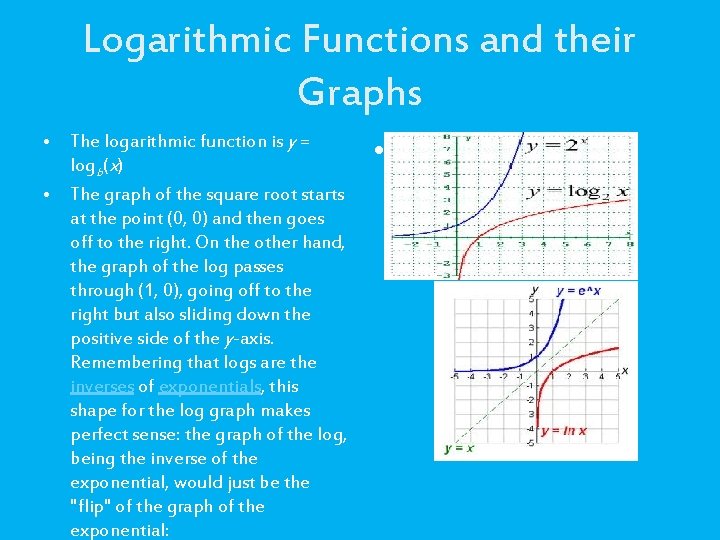
Logarithmic Functions and their Graphs • The logarithmic function is y = logb(x) • The graph of the square root starts at the point (0, 0) and then goes off to the right. On the other hand, the graph of the log passes through (1, 0), going off to the right but also sliding down the positive side of the y-axis. Remembering that logs are the inverses of exponentials, this shape for the log graph makes perfect sense: the graph of the log, being the inverse of the exponential, would just be the "flip" of the graph of the exponential: •

Properties of Logarithms • • • loga 1 = 0 because a 0 = 1 No matter what the base is, the log of 1 is always 0. That's because logarithmic curves always pass through (1, 0) loga a = 1 because a 1 = a Any value raised to the first power is that same value. loga ax = x The log base a of x and a to the x power are inverse functions. Whenever inverse functions are applied to each other, they inverse out, and you're left with the argument, in this case, x. loga x = loga y implies that x = y If two logs with the same base are equal, then the arguments must be equal. loga x = logb x implies that a = b If two logarithms with the same argument are equal, then the bases must be equal. •

Solving Exponential and Logarithmic equations • To solve an equation containing a variable exponent, isolate the exponential quantity. Then take a logarithm, to the base of the exponent, of both sides. • To solve an equation containing a logarithm, use the properties of logarithms to combine the logarithmic expressions into one expression. Then convert to exponential form and evaluate. Check the solution(s) and eliminate any extraneous solutions --recall that we cannot take the logarithm of a negative number. •

Parabolas • To make a parabola, you start with a line and a point off to one side. Which is the "directrix“. and point which is the "focus". The parabola is the graphed curve formed from all the points that are in the middle from the directrix and the focus. The line vertical to the directrix and passing through the focus is called the "axis of symmetry". The point on this axis which is exactly midway between the focus and the directrix is the "vertex“. Standard and vertex form Axis of Symmetry the equations for the vertex form of parabolas are: regular: y = a(x – h)2 + k sideways: x = a(y – k)2 + h

Hyperbolas • • A hyperbola is centered on the point (h, k), which is known as the center of the hyperbola. A hyperbola forms somewhat like an X when it is graphed. Hyperbolas share many of the ellipses' analytical properties such as eccentricity, focus, and directrix. Each branch of the hyperbola consists of two arms which become lower curvature more out from the center of the hyperbola. Diagonally opposite arms one from each branch tend in the limit to a common line, called the asymptote of those two arms. There are two asymptotes, their intersection is at the center of symmetry of the hyperbola, which can be thought of as the mirror point about which each branch reflects to form the other branch. In the case of the curve the asymptotes are the two coordinate axes. A hyperbola with center at the origin (0, 0), is the graph of

Ellipses • an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis. An ellipse is also the focus of all points of the plane whose distances to two fixed points add to the same constant. Ellipses are closed curves and are the bounded case of the conic sections, the curves that result from the intersection of a circular cone and a plane that does not pass through its apex.