Phy 212 General Physics II Chapter 16 Waves

Phy 212: General Physics II Chapter 16: Waves I Lecture Notes

Types of Waves Types of waves: a. Mechanical waves b. Electromagnetic waves c. Matter waves Classifying Waves: 1. Transverse Waves: oscillate perpendicular to the direction of wave propagation (examples: Light & E-M waves) 2. Longitudinal Waves: oscillate parallel to the direction of wave propagation (example: Sound)

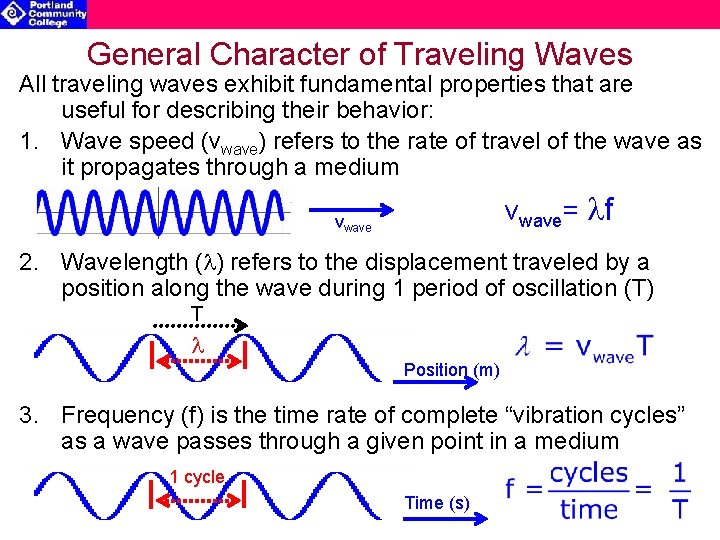
General Character of Traveling Waves All traveling waves exhibit fundamental properties that are useful for describing their behavior: 1. Wave speed (vwave) refers to the rate of travel of the wave as it propagates through a medium vwave= lf vwave 2. Wavelength (l) refers to the displacement traveled by a position along the wave during 1 period of oscillation (T) T l Position (m) 3. Frequency (f) is the time rate of complete “vibration cycles” as a wave passes through a given point in a medium 1 cycle Time (s)

Traveling Waves General form for the disturbance producing a traveling wave: Transverse Velocity: Velocity Amplitude: Acceleration: Acceleration Amplitude:

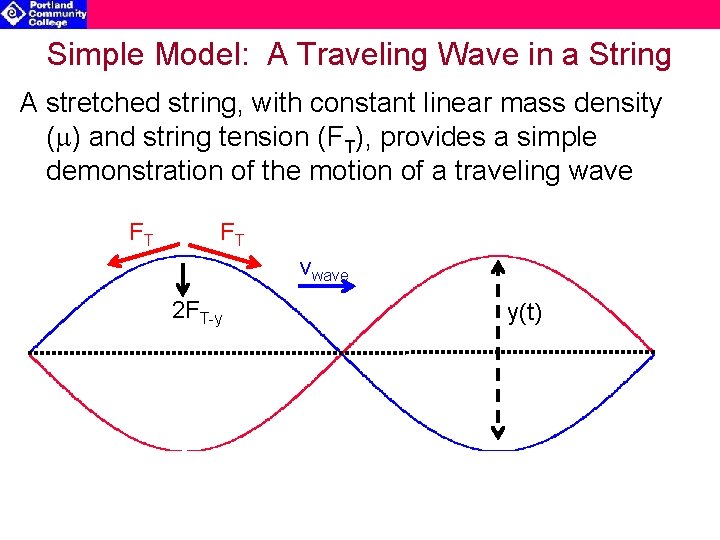
Simple Model: A Traveling Wave in a String A stretched string, with constant linear mass density (m) and string tension (FT), provides a simple demonstration of the motion of a traveling wave FT FT vwave 2 FT-y y(t)

Wave speed on Stretched String 1. 2. 3. 4. When a transverse disturbance travels along a taut string, the motion (transverse to the string) of any given segment of mass along the string oscillates in simple harmonic motion. The tension (FT ) in the string functions as an “elastic” force resulting in a traveling wave The linear mass density (m, in kg/m) of the string acts as the inertial element for the string which restricts the wave propagation. The wave speed along a string is therefore expressed as: Derivation:

Energy Transmission (Power) in Waves As a wave travels along the string, the total energy (d. Etot) for a string mass segment of length, dx, is the combination of both its K and U: where: The average energy is: where: d. K(t)avg = d. U(t)avg The average power is:

The Wave Equation 1. The motion of a traveling wave is dependent on both time and position: 2. This equation (and all equations) that describe traveling wave motion, must satisfy the wave equation:

Superposition of Waves & Interference Waves of the same type that cross paths do not alter the other. • They do appear to combine to produce a resulting wave that is a superposition of each wave. • For 2 identical waves (y 1 and y 2) that are out of phase, the resultant wave is given by: • The resultant wave is itself sinusoidal and its magnitude is depends on the phase difference between y 1 and y 2

Phasors are analogous to vectors and are useful for analyzing the superposition of same frequency traveling waves: y’ 1. A phasor is a vector representation of the magnitude (length) and phase (angular direction) for a wave 2. When 2 or more waves undergo interference, y 1 the magnitude and phase of the resultant (superimposed) wave can be determined by the vector addition of the corresponding phasors a. b. y 3 y 2 The resultant phasor magnitude is the magnitude of resultant wave The resultant phasor angle is the phase angle of resultant wave

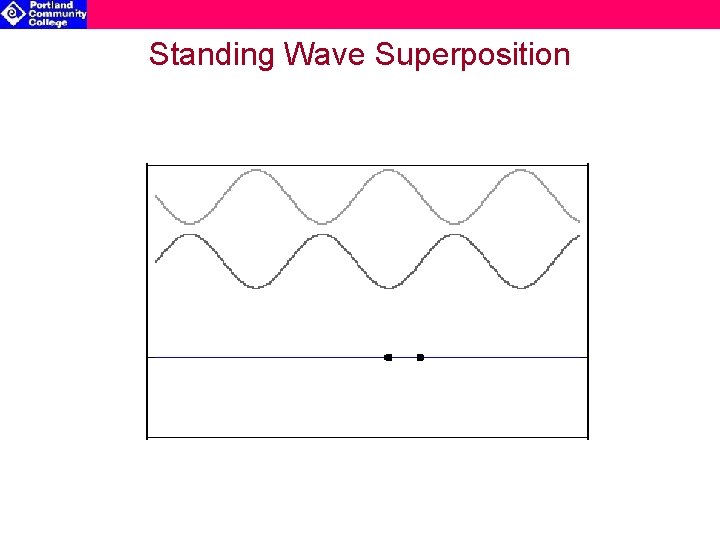
Standing Waves in a String 1. Standing waves are self-reinforcing waves produced by the constructive interference of a wave with its reflection. 2. Consider a wave traveling along a string (fixed at each end). When the wave reaches the end of the string it reflects back in the opposite direction (180 o out of phase). 3. The wave will produce a standing wave if the nodes for the resultant wave are stationary Condition for a standing wave: where: L is length of string n is the number of ½ wavelengths (l) n=1 n=2 n=3

Standing Wave Superposition