P 1 X Dynamics Relativity Newton Einstein Part

P 1 X Dynamics & Relativity: Newton & Einstein Part I - “I frame no hypotheses; Dynamics READ the textbook! section numbers in syllabus Motion Forces – Newton’s Laws Simple Harmonic Motion for whatever is not deduced from the phenomena is to be called a hypothesis; and hypotheses, whether metaphysical or physical, whether of occult qualities or mechanical, have no place in experimental philosophy. ” Circular Motion http: //ppewww. ph. gla. ac. uk/~parkes/teaching/Dynamics. html October 2007 Chris Parkes

Motion • Position [m] • Velocity [ms-1] – Rate of change of position x e. g dx 0 v dt t • Acceleration [ms-2] – Rate of change of velocity 0 a 0 t

Equations of motion in 1 D – Initially (t=0) at x 0 – Initial velocity u, – acceleration a, s=ut+1/2 at 2, where s is displacement from initial position Differentiate w. r. t. time: v=u+at v 2=u 2+2 as

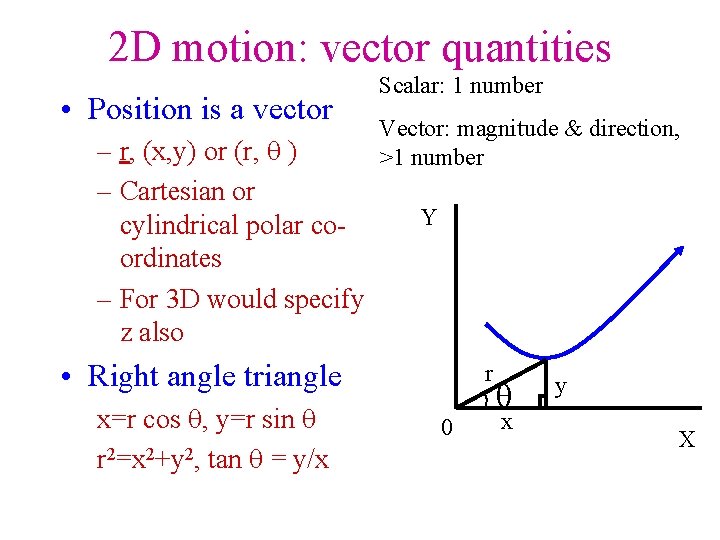
2 D motion: vector quantities • Position is a vector – r, (x, y) or (r, ) – Cartesian or cylindrical polar coordinates – For 3 D would specify z also Scalar: 1 number Vector: magnitude & direction, >1 number Y • Right angle triangle x=r cos , y=r sin r 2=x 2+y 2, tan = y/x r 0 x y X

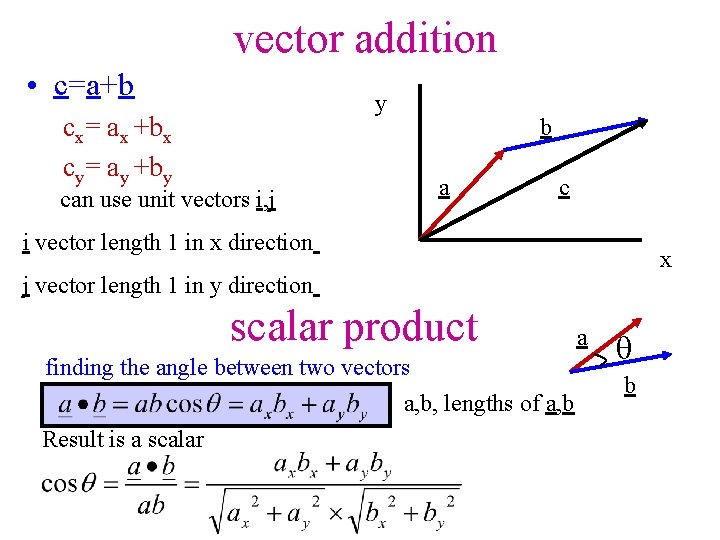
vector addition • c=a+b y cx= ax +bx cy= ay +by can use unit vectors i, j b a c i vector length 1 in x direction x j vector length 1 in y direction scalar product finding the angle between two vectors a, b, lengths of a, b Result is a scalar a b

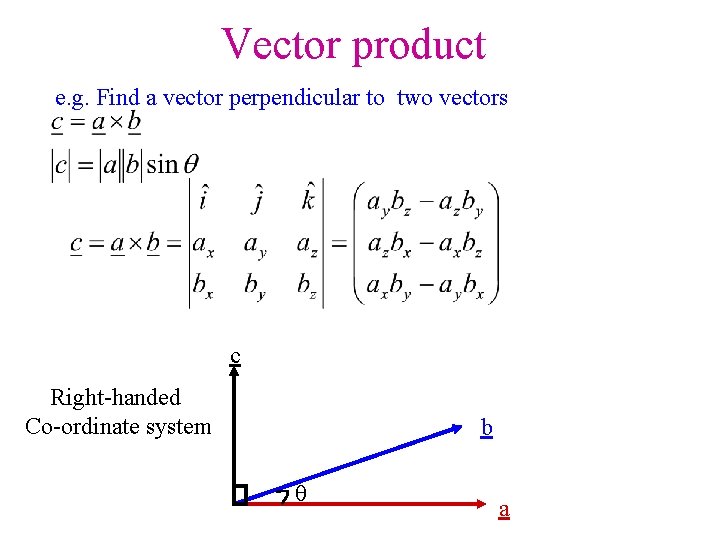
Vector product e. g. Find a vector perpendicular to two vectors c Right-handed Co-ordinate system b a

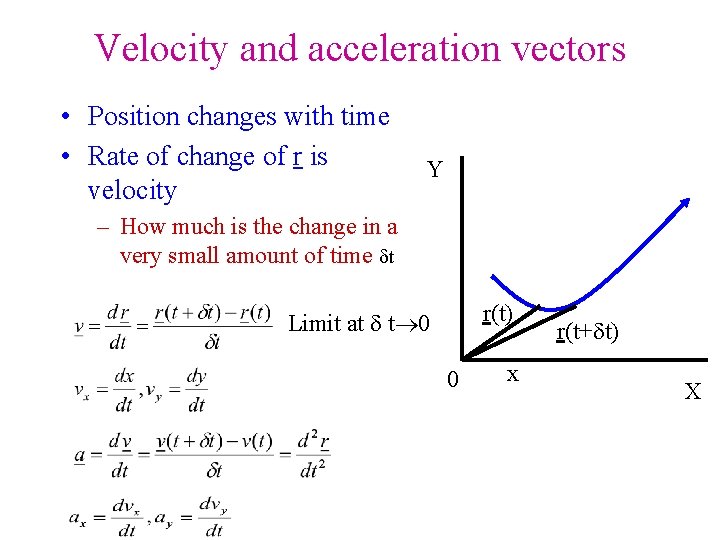
Velocity and acceleration vectors • Position changes with time • Rate of change of r is velocity Y – How much is the change in a very small amount of time t r(t) Limit at t 0 0 x r(t+ t) X

Projectiles Motion of a thrown / fired object mass m under gravity y Velocity components: v vx=v cos x, y, t vy=v sin x a: v=u+at: x direction ax=0 vx=vcos + axt = vcos s=ut+0. 5 at 2: x=(vcos )t Force: -mg in y direction acceleration: -g in y direction ay=-g vy=vsin - gt y= vtsin -0. 5 gt 2 This describes the motion, now we can use it to solve problems

Relative Velocity 1 D e. g. Alice walks forwards along a boat at 1 m/s and the boat moves at 2 m/s. What is Alice’s velocity as seen by Bob ? If Bob is on the boat it is just 1 m/s If Bob is on the shore it is 1+2=3 m/s If Bob is on a boat passing in the opposite direction…. . and the earth is spinning… Velocity relative to an observer Relative Velocity 2 D e. g. Alice walks across the boat at 1 m/s. V boat 2 m/s As seen on the shore: θ V relative to shore V Alice 1 m/s

Changing co-ordinate system Define the frame of reference – the co-ordinate system – in which you are measuring the relative motion. y (x’, y’) Frame S (shore) vt Frame S’ (boat) v boat w. r. t shore x’ x Equations for (stationary) Alice’s position on boat w. r. t shore i. e. the co-ordinate transformation from frame S to S’ Assuming S and S’ coincide at t=0 : Known as Gallilean transformations As we will see, these simple relations do not hold in special relativity

We described the motion, position, velocity, acceleration, now look at the underlying causes Newton’s laws • First Law – A body continues in a state of rest or uniform motion unless there are forces acting on it. • No external force means no change in velocity • Second Law – A net force F acting on a body of mass m [kg] produces an acceleration a = F /m [ms-2] • Relates motion to its cause F = ma units of F: kg. m. s-2, called Newtons [N]

• Third Law – The force exerted by A on B is equal and opposite to the force exerted by B on A Fb • Force exerted by Block on table block on table is F Fa=-Fb Weight (a Force) Fa • Force exerted by table on block is Fb (Both equal to weight) Examples of Forces weight of body from gravity (mg), - remember m is the mass, mg is the force (weight) tension, compression Friction, a

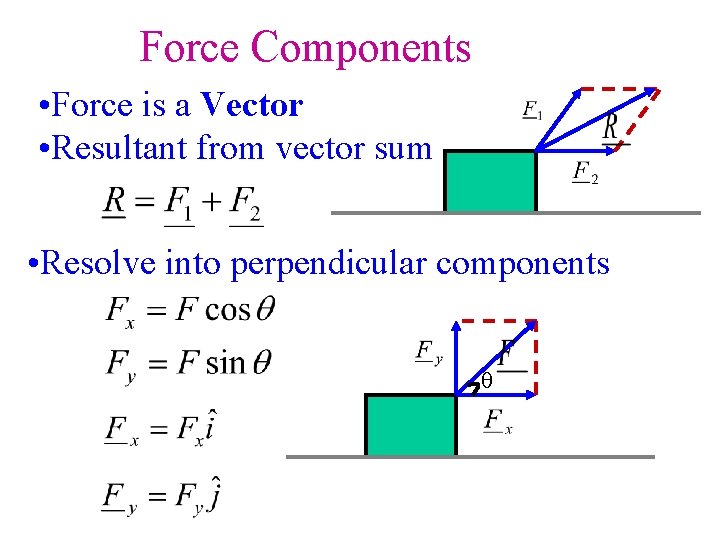
Force Components • Force is a Vector • Resultant from vector sum • Resolve into perpendicular components

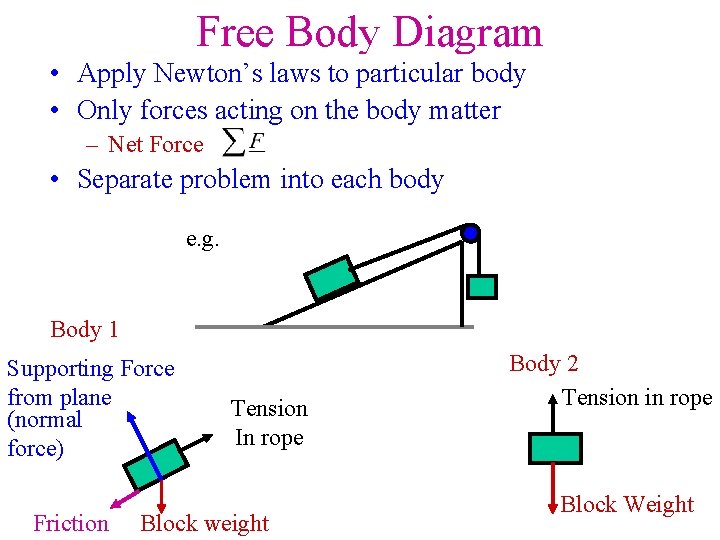
Free Body Diagram • Apply Newton’s laws to particular body • Only forces acting on the body matter – Net Force • Separate problem into each body e. g. Body 1 Supporting Force from plane (normal force) Friction Tension In rope Block weight Body 2 Tension in rope Block Weight

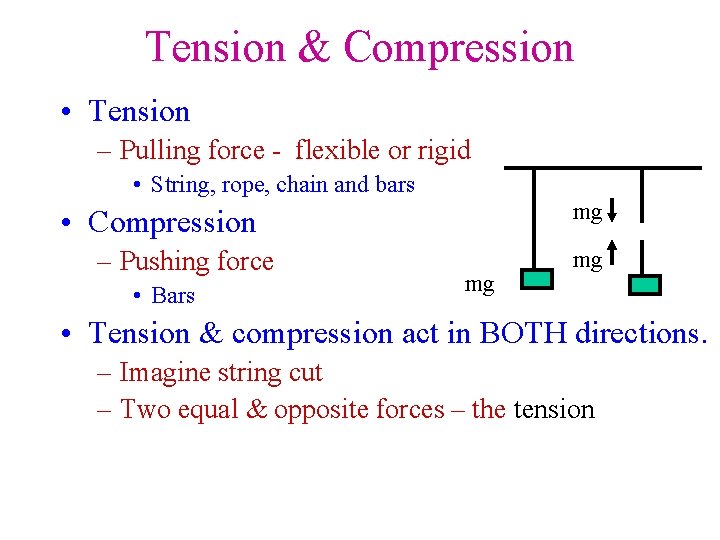
Tension & Compression • Tension – Pulling force - flexible or rigid • String, rope, chain and bars mg • Compression – Pushing force • Bars mg mg • Tension & compression act in BOTH directions. – Imagine string cut – Two equal & opposite forces – the tension

Friction • A contact force resisting sliding – Origin is chemical forces between atoms in the two surfaces. • Static Friction (fs) – Must be overcome before an objects starts to move • Kinetic Friction (fk) – The resisting force once sliding has started • does not depend on speed N fs or fk F mg

Simple Harmonic Motion Oscillating system that can be described by sinusoidal function Pendulum, mass on a spring, electromagnetic waves (E&B fields)… • Occurs for any system with Linear restoring Force » Same form as Hooke’s law – Hence Newton’s 2 nd – Satisfied by sinusoidal expression A is the oscillation amplitude is the angular frequency or – Substitute in to find in radians/sec Frequency Period Hz, cycles/sec Sec for 1 cycle

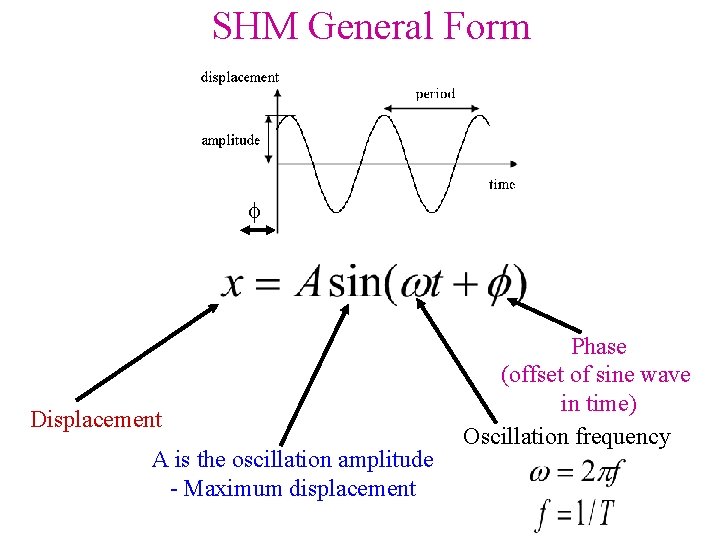
SHM General Form Displacement A is the oscillation amplitude - Maximum displacement Phase (offset of sine wave in time) Oscillation frequency

SHM Examples 1) Mass on a spring • Let weight hang on spring • Pull down by distance x – Let go! L’ In equilibrium F=-k. L’=mg Energy: x Restoring Force F=-kx (assuming spring has negligible mass) potential energy of spring But total energy conserved At maximum of oscillation, when x=A and v=0 Total Similarly, for all SHM (Q. : pendulum energy? )

SHM Examples 2) Simple Pendulum • Mass on a string L Working along swing: Not actually SHM, proportional to sin , not but if is small x c. f. this with F=-kx on previous slide mg sin mg Hence, Newton 2: and Angular frequency for simple pendulum, small deflection

Circular Motion 360 o = 2 radians 180 o = radians 90 o = /2 radians • Rotate in circle with constant angular speed R – radius of circle s – distance moved along circumference = t, angle (radians) = s/R • Co-ordinates x= R cos t y= R sin t y R s = t x t=0 • Velocity • Acceleration N. B. similarity with S. H. M eqn 1 D projection of a circle is SHM

Magnitude and direction of motion • Velocity v= R And direction of velocity vector v Is tangential to the circle • Acceleration v a a= 2 R=( R)2/R=v 2/R And direction of acceleration vector a a= - 2 r Acceleration is towards centre of circle

Force towards centre of circle • Particle is accelerating – So must be a Force • Accelerating towards centre of circle – So force is towards centre of circle F=ma= mv 2/R in direction –r or using unit vector • 1. 2. 3. Examples of central Force Tension in a rope Banked Corner Gravity acting on a satellite

Gravitational Force Myth of Newton & apple. He realised gravity is universal same for planets and apples • Any two masses m 1, m 2 attract each other with a gravitational force: F F r m 2 m 1 Newton’s law of Gravity Inverse square law 1/r 2, r distance between masses The gravitational constant G = 6. 67 x 10 -11 Nm 2/kg 2 • Explains motion of planets, moons and tides m. E=5. 97 x 1024 kg, RE=6378 km Mass, radius of earth Gravity on earth’s surface Or Hence,

N. B. general solution is an ellipse not a circle - planets travel in ellipses around sun Satellites • Centripetal Force provided by Gravity m R M Distance in one revolution s = 2 R, in time period T, v=s/T T 2 R 3 , Kepler’s 3 rd Law • Special case of satellites – Geostationary orbit • Stay above same point on earth T=24 hours

Dynamics I – Key Points 1. 1 D motion, 2 D motion as vectors – s=ut+1/2 at 2 v=u+at v 2=u 2+2 as – Projectiles, 2 D motion analysed in components 2. Newton’s laws – F = ma – Action & reaction 3. SHM 4. Circular motion (R, ) Oscillating system that can be described by sinusoidal function Force towards centre of circle