Nemlineris programozs Jtkelmlet Alkalmazott opercikutats 8 elads 20072008

Nemlineáris programozás Játékelmélet Alkalmazott operációkutatás 8. előadás 2007/2008. tanév 2008. március 31.

Gyakorlás – tk. 124. oldal • 6 munkafeladat, 4 munkás • 4. és 6. munkafeladatot mindenképpen el kell végezni • Az 1. munkás a 3. és 6. munkafeladatot nem végezheti. • A 2. munkás az 1. és 4. munkafeladatot nem végezheti. • Határozzuk meg az elosztási tervet úgy, hogy az összköltség a legkisebb legyen!

Feladat – tk. 126. oldal • • Lovasverseny – 4 lovas – 4 ló Tibi, Béla, Pali, Zoli – A, B, C, D ló Pontátlagok az eddig szerzett pontok alapján Mi az a minimum pontszám, aminek az elérése mindenképpen várható? • Mennyi pontot szerezhetnek maximum?

Nemlineáris programozás • Célfüggvény nem lineáris (feltételek lineárisak) • Közgazdaságtanban ez szinte mindig így van, pl. ár-keresleti görbe • Nincs közös megoldási algoritmus (speciális megoldási algoritmusok) • Osztályozás: célfüggvény alapján – Célfüggvény másodfokú => kvadratikus programozás – Célfüggvény lineáris törtfüggvény => tört vagy hiperbolikus programozás

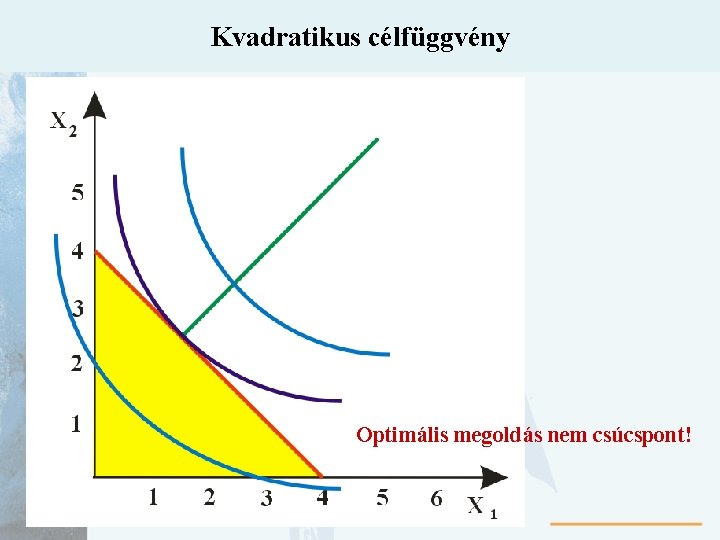
Kvadratikus célfüggvény Optimális megoldás nem csúcspont!

Tört vagy hiperbolikus program • Definíció: Hiperbolikus programozásról beszélünk akkor, ha lineáris feltételrendszer nemnegatív megoldásait tartalmazó halmaz felett olyan racionális törtfüggvény maximumát keressük, amelyben mind a számláló, mind a nevező első fokú függvény. • Megoldás: – Martos-féle módszer – Lineáris programozási feladattá transzformálás

Játékelmélet

Játékelmélet – alapfogalmak I. • Definíció: A játékelmélet olyan matematikai elmélet, amely vetélkedési helyzetek általános jellegzetességeivel foglalkozik. – kétszemélyes játék – n-személyes játék • Feltételek: – Racionális gondolkodás – Saját érdekek – Stratégia választás az ellenfél stratégiájának ismerete nélkül • Definíció: A stratégia egy előre kimondott szabály, amely meghatározza, hogyan válaszol a játékos a játék minden egyes szakaszában minden egyes körülményre. • Szóba jövő stratégiák összessége = stratégia halmaz Smahó Melinda

Játékelmélet – alapfogalmak II. • Definíció: Ha a játékosok egymástól függetlenül, csak a saját érdekük figyelembevételével választanak stratégiát, akkor nemkooperatív, egyébként kooperatív játékról beszélünk. • Játék kimenetele – Értékelő függvény – Kifizető mátrix • Ha a stratégiák halmaza véges, akkor véges játékról, egyébként végtelen játékról beszélünk. Smahó Melinda

Kétszemélyes zérusösszegű játékok • 2 játékos, az egyik játékos azt nyeri, amit a másik elveszít • Példa: egy J 1 játékos és egy J 2 játékos felmutatja egyszerre egy vagy két ujját. Ha az ujjak száma megegyezik, akkor J 1 játékos nyer, ha nem, akkor veszít. A játék kifizetési táblázata J 1 játékos számára: Smahó Melinda

Mátrixjáték egyensúlyi pontja / nyeregpontja • Mátrixjáték: kétszemélyes zérusösszegű véges játék

Kevert stratégiájú mátrixjátékok • Tiszta stratégia: ha játékos a játékban egy oszlopot vagy sort választ és végig ezzel a stratégiával játszik. • Kevert/súlyozott stratégia: a játékosok változtatják a stratégiát a játék során.

Kétszemélyes nem konstans összegű játékok • Kooperatív nem konstans összegű játék: játékosok együttműködnek, együttes nyeremény szétosztása (J. Nash, R. Selten, Harsányi J. ) 1928 - 1930 - 1920 - 2000 • Nem kooperatív nem konstans összegű játék: játékosok nem működnek együtt

Nash-egyensúly: J 2 adott választása mellett J 1 döntése optimális és J 1 döntése esetén J 2 döntése optimális. (egyik sem tudja előre, hogy mit választ a másik).

Fogoly-dilemma B játékos Vall A játékos Tagad Vall Tagad Nash-egyensúly: ha mindketten vallanak Pareto-hatékony: ha mindketten tagadnak (mindketten jobban járnak) Nash-egyensúly nem mindig Pareto-hatékony!

Szállítási feladat Az R 1, R 2, R 3, R 4 jelű vegyesboltok péksüteménnyel való ellátását az F 1, F 2, F 3 jelű pékségekből biztosítják. Az egyes boltok napi péksüteményigénye rendre (sorrendben) 30, 80, 50, 40 kg. A pékségek napi teljesítménye rendre (sorrendben) 90, 70, 40 kg. Az egyes Ri-Fi viszonylatokban érvényes fajlagos szállítási költséget (Ft/kg) az alábbi táblázat mutatja. • Feladatok: • a) Oldjuk meg a feladatot soroszlopminimum módszerrel! • b) Határozzuk meg az előállított lehetséges megoldáshoz tartozó szállítási költséget!

Köszönöm a figyelmet!