Module 3 3 Tick TockThe Pendulum Clock Angela

Module 3. 3 Tick Tock—The Pendulum Clock Angela B. Shiflet and George W. Shiflet Wofford College © 2014 by Princeton University Press

Introduction • The first pendulum clock built by a Dutch scientist Christiaan Huygens in 1656 was incredibly accurate (losing less than a minute each day). • Galileo is usually credited with the invention of the pendulum during the sixteenth century. Galileo studied gravity used the motion of a pendulum although the common myth is that he studied the gravity by dropping objects from the top of the Leaning Tower of Pisa.

Introduction • Physicists use the pendulum as a classic example of energy conservation. • Mechanical energy is equal to the total of kinetic (½mv 2) and potential energy (due to gravity m*g*h), assuming no friction in the air, and is always constant during the oscillation of the pendulum. • If you pull up the mass, you increase the potential energy. When you release it, the potential energy decreases as the mass (bob) fall, but the kinetic energy increases as the speed of the mass increases.

Simple pendulum • Simplifying assumptions • All mass for bob concentrated at point • Stiff string has no mass • Friction does not exist

Simple pendulum equations • Tangential component of the weight • -mg sinϕ (because it points to the left when ϕ > 0 and points to the right when ϕ <0) • Arc length from bob to vertical • lϕ • Angular acceleration • d 2(lϕ)/dt 2 = l d 2(ϕ)/dt 2 • Force by Newton's Second Law of Motion • F = ma = ml d 2(ϕ)/dt 2

Simple pendulum equations • Equate forces : ml d 2(ϕ)/dt 2 = -mg sinϕ • Solve for angular acceleration • Angular acceleration d 2(ϕ)/dt 2 = -g sinϕ/l • Initial angular velocity = d(ϕ)/dt = 0 This ODE is non-linear. We can approximate it by letting sinϕ ≈ ϕ.

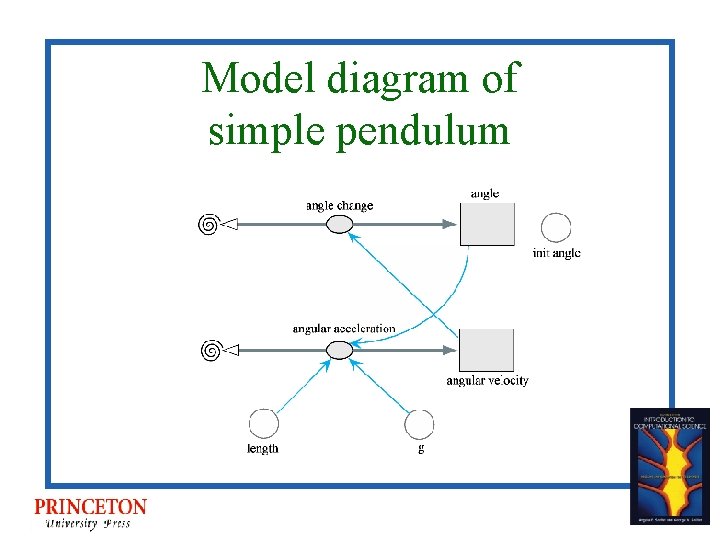
Model diagram of simple pendulum

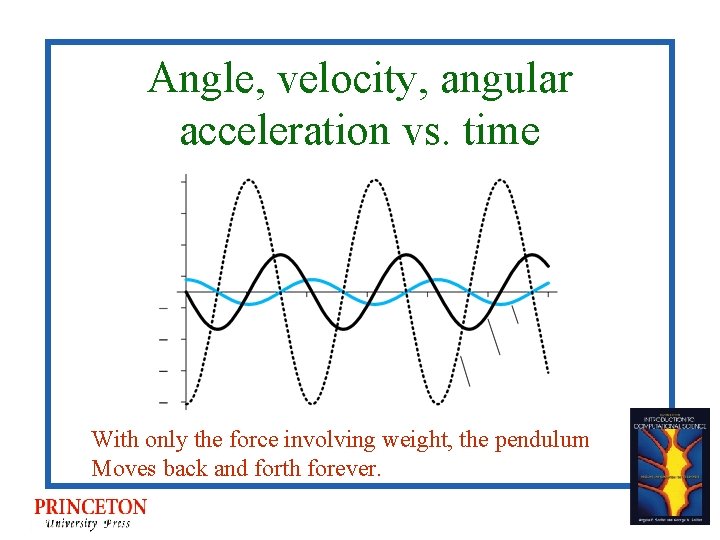
Angle, velocity, angular acceleration vs. time With only the force involving weight, the pendulum Moves back and forth forever.

Linear damping ml d 2(ϕ)/dt 2 = -mg sinϕ – kd(ϕ)/dt Initial condition: ϕ = ϕ 0 and d(ϕ)/dt |t =0= 0 Þd 2(ϕ)/dt 2 + (k/(m*l)) *d(ϕ)/dt + (g/l)*sinϕ = 0 This is a non-linear second order ODE. We can approximate the solution by letting sinϕ ≈ ϕ.

Linear damping • Linear friction (use Stokes’ friction F = kv) • kd(ϕ)/dt • Incorporate friction as another force • ml d 2(ϕ)/dt 2 = -mg sinϕ – kd(ϕ)/dt • Initial condition: ϕ = ϕ 0 and d(ϕ)/dt |t =0= 0 • Note that the angle ϕ of a pendulum does not affect its period, or the length of the time to complete a full cycle.

Pendulum clock