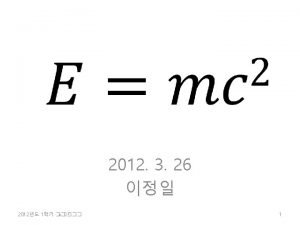Module 1 Newtonian Relativity The Galilean Transformation Equations

Module 1 Newtonian Relativity The Galilean Transformation Equations What do we mean by a “theory of relativity”? Let’s discuss the matter using conventional terminology. An observer measures an event in the observer’s frame of reference. The frame of reference is the spatial and temporal coordinate system used by the observer. An event is something that happens and is observed by the observer. It can be anything, a light going on, a light going off, a clap, or simply the occupation of some spatial point at some time by an object. The event is described by the observer by three spatial coordinates (location) and one temporal coordinate (time of occurrence). Using a Cartesian coordinate system, you can represent the frame of reference as shown below in Figure 1 -1. Let’s call the frame of reference S. You can imagine the observer situated at the spatial origin O with a clock to measure time. An event, then, is described by the four coordinates (x, y, z, t). y S Event (x, y, z, t) 0: 00 x O z Module 1 Newtonian Relativity Fig. 1 -1 1

Now imagine that there is another observer moving relative to the first observer. This observer has his own frame of reference. Let’s call it S’. This observer, situated at the origin O’, sees the same event occur and measures (x’, y’, z’, t’) for the event. The purpose of a theory of relativity is to relate the coordinates measured in frame S to those measured in frame S’ for the same event. That’s it, plain and simple. I have to admit that theory is richer than this may sound since many other physical quantities are found from position and time. A relativity theory will also relate quantities like velocity, acceleration, momentum, and energy. Let’s set up the geometry of the two frames that we’ll use throughout the course. We will make the x-axis of frame S and the x’-axis of frame S’ be collinear and always point in the direction of the relative motion between the frames. The relative speed between the frames is v and frame S’ moves to the right relative to S. We’ll also make the times measured in both frames be zero when the origins coincide. Figure 1 -2 shows our conventional geometry. I find it helpful to imagine the two observers at rest in their respective frames at the origins. In fact, let’s give the observers names. Let’s call the observer in S Unprime and the observer in S’ Prime. So we can picture Unprime sitting at origin O, Prime sitting at origin O’, and Prime moving to the right at speed v relative to Unprime. y y’ S S’ v O z Module 1 x O’ z’ Newtonian Relativity x’ Fig. 1 -2 2

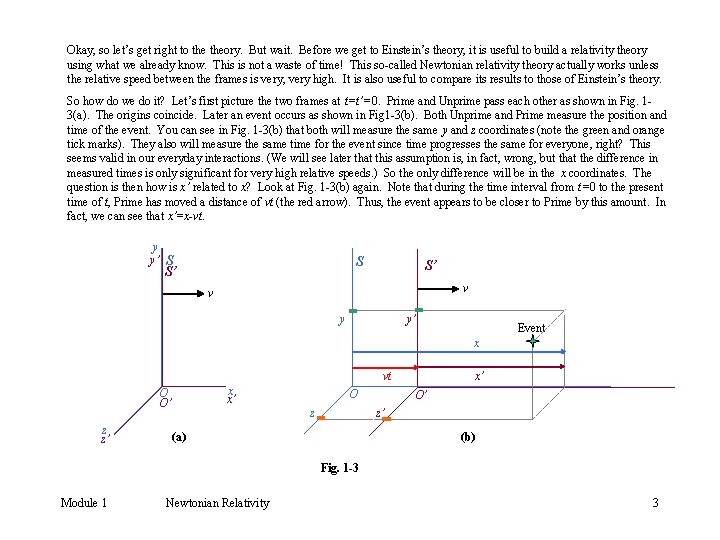
Okay, so let’s get right to theory. But wait. Before we get to Einstein’s theory, it is useful to build a relativity theory using what we already know. This is not a waste of time! This so-called Newtonian relativity theory actually works unless the relative speed between the frames is very, very high. It is also useful to compare its results to those of Einstein’s theory. So how do we do it? Let’s first picture the two frames at t=t’=0. Prime and Unprime pass each other as shown in Fig. 13(a). The origins coincide. Later an event occurs as shown in Fig 1 -3(b). Both Unprime and Prime measure the position and time of the event. You can see in Fig. 1 -3(b) that both will measure the same y and z coordinates (note the green and orange tick marks). They also will measure the same time for the event since time progresses the same for everyone, right? This seems valid in our everyday interactions. (We will see later that this assumption is, in fact, wrong, but that the difference in measured times is only significant for very high relative speeds. ) So the only difference will be in the x coordinates. The question is then how is x’ related to x? Look at Fig. 1 -3(b) again. Note that during the time interval from t=0 to the present time of t, Prime has moved a distance of vt (the red arrow). Thus, the event appears to be closer to Prime by this amount. In fact, we can see that x’=x-vt. y y’ S S S’ S’ v v y y’ Event x x’ vt x x’ O O’ z z’ O z O’ z’ (b) (a) Fig. 1 -3 Module 1 Newtonian Relativity 3

We can then write down the following group of relativity relations: (1. 1) These set of relations are called the Galilean transformation equations. Any theory of relativity is described by a set of transformation equations. Newtonian relativity uses the Galilean transformation equations. From these basic equations, you can then relate other physical quantities that the observers measure. For instance, suppose that an object is moving in both frames of reference and that both Unprime and Prime measure its velocity and acceleration. You can derive the velocity and acceleration transformation equations from Eqs. (1. 1). You will do this in Problem 1. 1 and will show that (1. 2) and (1. 3) Module 1 Newtonian Relativity 4

In the subsequent problems of Module 1, you will compare other physical quantities of an object measured by the two observers. You will see that even though the two observers measure different speeds, different distances traveled, different momenta, and different energies for the same objects, each observer measures the same acceleration and force acting on a particular object and each observer sees energy and momentum conserved. This is what we mean when we say that the laws of mechanics are invariant in Newtonian relativity. One last note before we move on to the next section. We have assumed in our discussion that the relative velocity is a constant. That is, Prime always move in the same direction relative to Unprime and at the same speed v. This makes the two frames of S and S’ inertial frames of reference and theory a special relativity theory. We will assume that this is the case throughout this course. If the relative velocity does change, the frames are not inertial frames of reference and the relationships between the quantities measured by the observers can be different than we derive here. The Space-time Four-vector and Matrix Representation You are use to dealing with three-dimensional vectors, like position, which has three orthogonal components which we can specify with the form (x, y, z). Now imagine that we add another orthogonal component to make a four-dimensional vector. Let’s make this component ct where c is a constant. We multiply time by c to make this fourth component have the same units as the other three components, namely units of length. This constant has units of speed and one could let it be equal to the speed of light in vacuum, but that’s not important right now. As long as c is a constant, it’s value doesn’t really matter at this point. It is difficult to visualize this fourth component, no doubt, as who can imagine four perpendicular axes? But we can still do it mathematically. In fact, we can have a vector with N orthogonal components if we want. We now recognize that the four components of this vector give the position and time of an event measured by Unprime. We call this vector the space-time four-vector since its four components specify the spatial position and time of a measured event. Let’s denote it by the vector symbol tau, (1. 4) Module 1 Newtonian Relativity 5

It follows that there is a corresponding space-time four vector whose components are the position and time measured by Prime for the same event, (1. 5) In terms of a vector picture, note that the Galilean transformation equations take the tau vector and change it into the tau prime vector. This a vector operation. The Galilean transformation equations can be thought of as a vector operator. If we symbolize this operator by G, we can represent the transformation by (1. 6) We can describe G further by using a matrix representation. To do this, we do need to recall how matrices multiply each other. Suppose we have a matrix with two rows and one column. (A matrix with one column is called a column vector. ) Let’s call the two elements of the matrix x and y. Let’s multiply this matrix by another matrix with two rows and two columns. Let’s call the elements of this matrix a, b, c, and d. The rules of matrix multiplication dictate that the product of these two matrices is a column vector with two rows whose elements are specified in Eq. (1. 7) Note that to get the first element in the product matrix, you take the first row of the first matrix and “multiply” it by the column of the column vector as indicated below with the red lines. Similarly, you “multiply” the second row of the matrix by the column of the column vector to get the second row of the product matrix. Module 1 Newtonian Relativity 6

We can represent the two space-time vectors as two column vectors with four elements in each. Then Eq. (1. 6) looks like (1. 8) It follows that G must be a four-by-four matrix (four rows and four columns). What are the elements of G? You should prove to yourself using the Galilean transformation equations that the matrix G must be given by (1. 9) One more word about viewing G as a vector operator. Note that when it operates on the tau vector to give the tau prime vector, it changes only one component, namely the x-component. Thus, the tau prime vector does not have the same magnitude as the tau vector. The magnitude of a four-vector is simply the square root of the sum of the squares of its components, just like for an ordinary three-dimensional position vector. Specifically, the squares of the magnitudes of the tau and tau prime vectors are given by t 2 = x 2 + y 2 + z 2 + c 2 t 2 and t’ 2 = x’ 2 + y’ 2 + z’ 2 + c’ 2 t’ 2. The fact that the magnitudes of the vectors are not the same makes us say that the space-time four-vector is not invariant under Newtonian relativity. The ideas of four-vectors and representing transformation equations by matrix vector operators will prove useful later when we discuss Einstein’s theory. Module 1 Newtonian Relativity 7