ME 321 Kinematics and Dynamics of Machines Steve
- Slides: 16
ME 321 Kinematics and Dynamics of Machines Steve Lambert Mechanical Engineering, U of Waterloo 9/17/2020
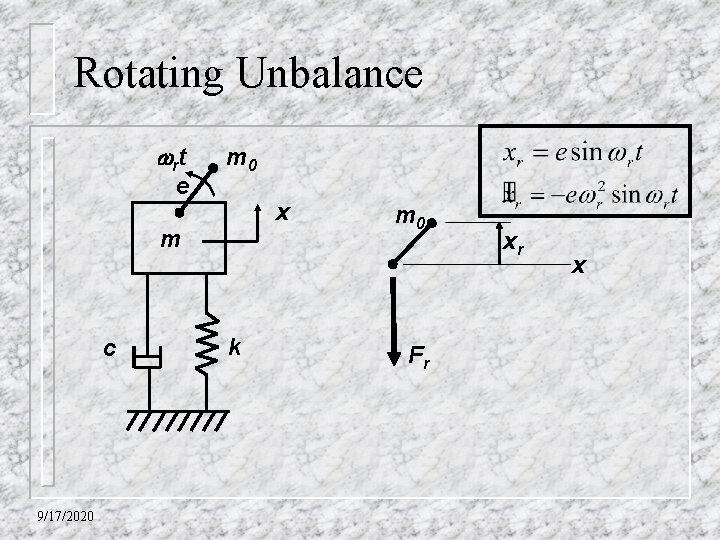
Rotating Unbalance r t e m 0 x m c 9/17/2020 k m 0 Fr xr x
Rotating Unbalance Equations of Motion: For the unbalanced mass: For the net mass: 9/17/2020
Rotating Unbalance Assume a particular solution of the form: By analogy to earlier solutions: and for r = r/ n 9/17/2020
Rotating Unbalance 9/17/2020
Rotating Unbalance Example 6. 5: A machine has a rotating unbalance, which results in a maximum steady-state deflection of 1 cm at resonance. Based on a measurement of the free decay of the system, it is estimated that the damping ratio is = 0. 1. The total mass of the system is 100 kg, and it is estimated, from manufacturing considerations, that the magnitude of the mass unbalance is 5 kg. Estimate the effective radius, e of the unbalance, and the amount of mass that would have to be added to the machine to reduce the vibration to 1 mm. 9/17/2020
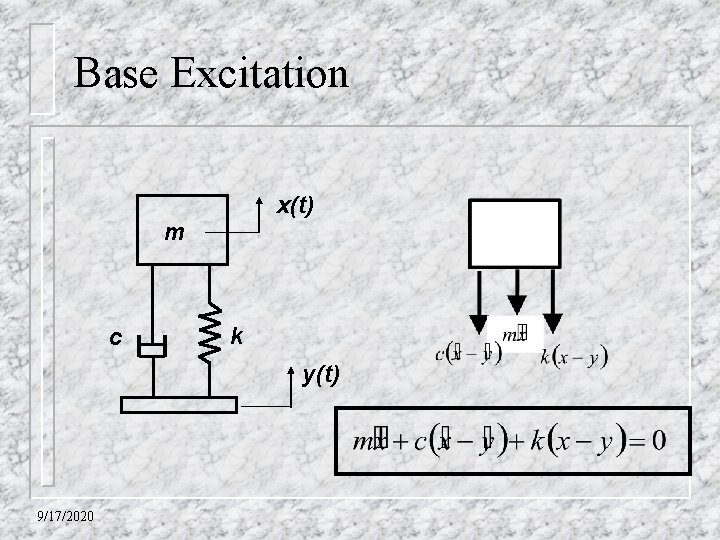
Base Excitation x(t) m c k y(t) 9/17/2020
Base Excitation Assume a base excitation of the form: This gives the following governing differential equation: Or, in normalized form: 9/17/2020
Base Excitation There are two particular solutions. One due to the force of the damper: And one due to the force of the spring: 9/17/2020
Base Excitation These two solutions have the same frequency, and can be combined as follows: 9/17/2020
Base Excitation Displacement transmissibility: 9/17/2020
Base Excitation The force acting on the mass through the damper and spring is: or: 9/17/2020
Base Excitation The transmitted force can be rewritten as: with: or, in normalized form: 9/17/2020
Base Excitation Force transmissibility: 9/17/2020
Base Excitation Force transmissibility (dashed line) and displacement transmissibility (solid line) for = 0. 05 9/17/2020
Base Excitation Example 6. 6: Consider a single degree-of-freedom model of an automobile suspension travelling over a rough road. The road is modeled as providing a base excitation, in m, of The equivalent stiffness of the suspension is k = 4 105 N/m, a damping coefficient, c = 40 103 kg/s, and a mass of 1000 kg. Determine the steady-state amplitude and displacement of the automobile mass. 9/17/2020
Kinematics and dynamics of machines
Aplusphysics kinematics-horizontal kinematics
Kinematics acceleration formula
Dynamics kinematics
Curvilinear translation
Ronald wayne biography
Dynamics of machines
Dynamics of machines
Pivoted cradle balancing machine
Kinematics and kinetics of rigid bodies
Linear and angular kinematics
Closed kinematic chain
Edel 321
Responsibilities
Csi 321
123 132 213 231 312 321
Apokalypsis 321
