ME 321 Kinematics and Dynamics of Machines Steve
















- Slides: 16

ME 321 Kinematics and Dynamics of Machines Steve Lambert Mechanical Engineering, U of Waterloo 2/22/2021

Kinematics and Dynamics l l Position Analysis Velocity Analysis Acceleration Analysis Force Analysis We will concentrate on four-bar linkages 2/22/2021

Velocity Analysis l l 2/22/2021 Can use vector methods or instantaneous centres Vector equations can be expressed in general form, or specialized for planar problems Ô Graphical Solutions Ô Vector Component Solutions Ô Complex Number Solutions

Vector Equations 2/22/2021

Vector Equations for Velocity Differentiate Position Vector with respect to Time 2/22/2021

Vector Velocity Equation Where: = Total absolute velocity of point = Absolute velocity of local origin = Relative velocity in local system = Angular velocity of Local System = Position of point in local system 2/22/2021

Planar Velocity Equations Assume: • Motion is restricted to the XY plane • Local frame is aligned with and fixed to link Therefore: • becomes the angular velocity of the link 2/22/2021

Planar Velocity Equations Becomes: 2/22/2021

Application to Four-Bar Linkages 2/22/2021

Graphical Solution 2/22/2021

Velocity Image A’B’ is the velocity image of link AB And then the velocity of point C, VC, can be obtained directly from the figure as the vector O’C’ 2/22/2021

Vector Component Solution But: and Giving: or: 2/22/2021

Instant Centres An instant centre is a point at which there is no relative velocity between two links in a mechanism, at a particular instant in time 2/22/2021

Kennedy’s Theorem Kennedy’s theorem states: the three instant centres of three bodies moving relative to one another must lie along a straight line. 2/22/2021

Kennedy’s Theorem 2/22/2021

Instant Centre Velocity Analysis 2/22/2021
 Kinematics and dynamics of machines
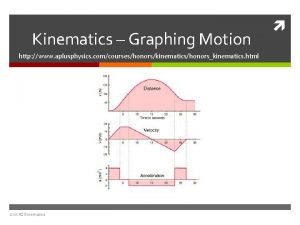
Kinematics and dynamics of machines Aplusphysics kinematics-horizontal kinematics
Aplusphysics kinematics-horizontal kinematics Kinematic equaitons
Kinematic equaitons A tourist being chased by an angry bear
A tourist being chased by an angry bear Rigid planar
Rigid planar Steve jobs steve wozniak ronald wayne
Steve jobs steve wozniak ronald wayne Dynamics of machines
Dynamics of machines Dynamics of machines
Dynamics of machines Pivoted cradle balancing machine
Pivoted cradle balancing machine Kinematic of rigid body
Kinematic of rigid body Linear and angular kinematics
Linear and angular kinematics Closed kinetic chain definition
Closed kinetic chain definition Edel 321
Edel 321 Responsibilities
Responsibilities Csi 321
Csi 321 123 132 213 231 312 321
123 132 213 231 312 321 Apokalypsis 321
Apokalypsis 321