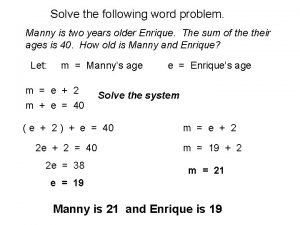Mathematic Problem Solving Learning to solve problems is

Mathematic Problem Solving Learning to solve problems is the principal reason for studying mathematics. (National Council of Supervisors of Mathematics (22) By: Rini, Julianty, Palupi Mentor : Sam

Issue Most of the students have difficulties to solve maths problems.

Why is teaching problem solving important? • It is an interesting and enjoyable way to learn mathematics; because the problems are the real life context • It produces positive attitudes towards mathematics • It teaches thinking, flexibility and creativity; because through problem solving, students can explore their ideas and creativity • It teaches general problem solving skills; because there are different strategies to solve the problems • It encourages cooperative skills; (students can work in pairs or groups to solve the problems) • It is a useful way to practice and apply mathematical skills

Objective To find out the effective strategies to help students solve maths problems independently.

Research Question What strategies are needed to improve students’ skills in solving maths problems?

Data Collection and Analysis 1. Do survey Give students a problem (in grade 3, 4 and 6) and let them solve it using steps ( fact, question, strategy used, how to solve and conclusion) Criteria for assessment: • Understanding of the problem • Deciding appropriate strategies • Explaining the way of thinking • Calculating accurately • Time needed 2. Observations of applying solving problems strategies

From the observations, the problems that students face when they solve Math problems are: • Reading the problems (more on reading comprehension)- language barrier • Identifying math operations (convert vocabs into symbols) • Some students tend to do skimming. They do not read the problems carefully, so they miss out the important element of problems. • Most of students tend to use algorithm way rather than other strategies, as they think problem solving always dealing with numbers. • Having difficulties in deciding the appropriate strategy and explaining the way of thinking. • Confidence to share their understanding (some students try to make sure their understanding to teacher(s)

Strategies Used to Improve Students’ Skills in Solving Maths Problem Solving • Pair up students to solve particular problems (different ability) • Recall some vocabs that can be transferred into symbols (gain, lost, sum, total, etc) • Reading comprehension with CUBES strategies (circle, underline, box, evaluate and solve) and break down all understanding in form of fact, question, solution and conclusion. • Visualize the problem (words, numbers, symbols, diagrams and models) • Use Thinking and Solution Chart • Teach every strategy of solving problems in particular time for some questions that are best solved with this strategy. Then at the last we give students problems that require different strategies to solve them.

CUBES C = circle the key numbers U = underline the question B = box math action words E = evaluate (what steps do I take) S = solve and check

Visualize the Problem Alex needed a square area for his chickens. If he used 24 fence posts, how many are there on each side? Read it again. Alex needed a square area for his chickens. If he used 24 fence posts, how many are there on each side? Highlight the important information Alex needed a square area for his chickens. If he used 24 fence posts, how many are there on each side? Restate the problem in your own words How many fence-posts are on each side of a square? There are 24 posts altogether. Identify any key words I need to understand Square is an important word in this problem. I know that a square has all four sides the same.
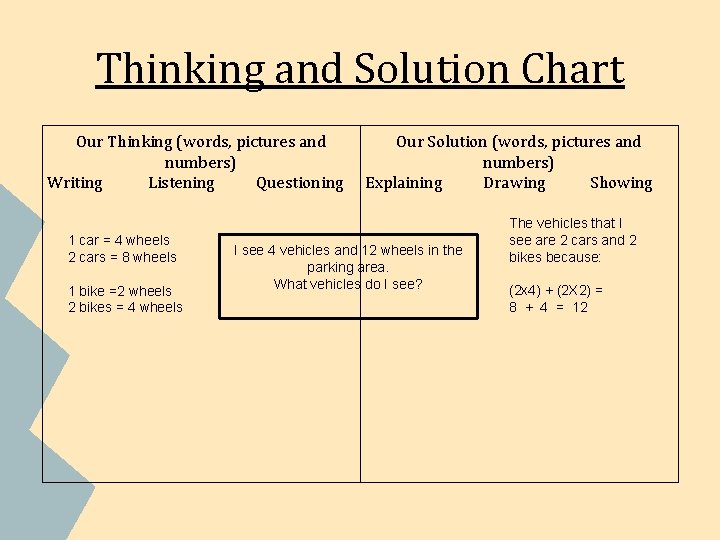
Thinking and Solution Chart Our Thinking (words, pictures and numbers) Writing Listening Questioning 1 car = 4 wheels 2 cars = 8 wheels 1 bike =2 wheels 2 bikes = 4 wheels Our Solution (words, pictures and numbers) Explaining Drawing Showing I see 4 vehicles and 12 wheels in the parking area. What vehicles do I see? The vehicles that I see are 2 cars and 2 bikes because: (2 x 4) + (2 X 2) = 8 + 4 = 12
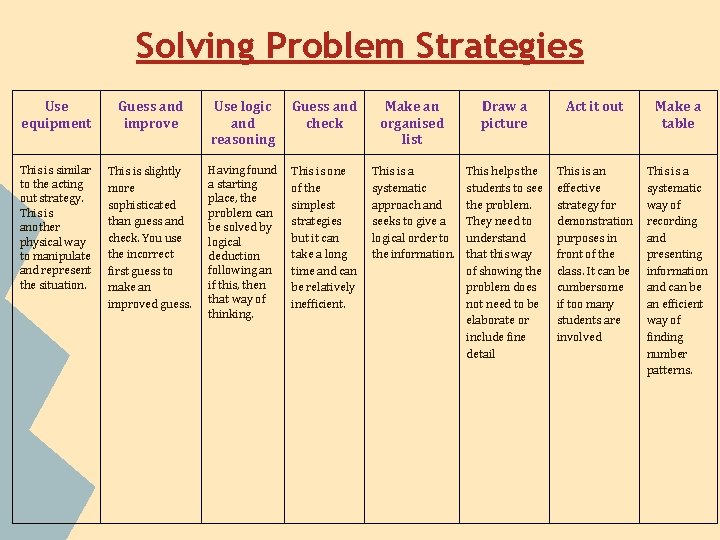
Solving Problem Strategies Use equipment Guess and improve Use logic and reasoning Guess and check Make an organised list Draw a picture Act it out Make a table This is similar to the acting out strategy. This is another physical way to manipulate and represent the situation. This is slightly more sophisticated than guess and check. You use the incorrect first guess to make an improved guess. Having found a starting place, the problem can be solved by logical deduction following an if this, then that way of thinking. This is one of the simplest strategies but it can take a long time and can be relatively inefficient. This is a systematic approach and seeks to give a logical order to the information. This helps the students to see the problem. They need to understand that this way of showing the problem does not need to be elaborate or include fine detail This is an effective strategy for demonstration purposes in front of the class. It can be cumbersome if too many students are involved This is a systematic way of recording and presenting information and can be an efficient way of finding number patterns.

Bibliography • http: //www. nzmaths. co. nz/bracken/pd/Teaching_Problem_Solving/Teachin g_Problem_Solving. html • http: //www. majortests. com/sat/problem-solving. php • www. mathplayground. com/wordproblems. html • www. kidsmathgamesonline. com/problemsolving. html • Chanda Pinsent, International Mathematics Consultant, New Zealand, in “Pedagogical Content Knowledge and Planning for Learning in Mathematics” September 30 -October 11, 2013. • Grade 3 A, 4 A and 6 D students, survey and observations term 2 -3, 2013 -2014

Reflection • We used more qualitative data analysis, so we don’t have the exact data to measure the success of our research. We consider to use quantitative data as well for further research. • We focused on students difficulties in solving problems, somehow teacher(s)’s plan, knowledge and skills contribute to the success of students in solving problems.
- Slides: 14