Solve direct and inverse proportion problems Solve problems

Solve direct and inverse proportion problems Solve problems involving direct and inverse proportion, including graphical and algebraic representations If you have any questions regarding these resources or come across any errors, please contact helpful-report@pixl. org. uk

Key vocabulary Inverse Direct Proportional Equation Constant Value
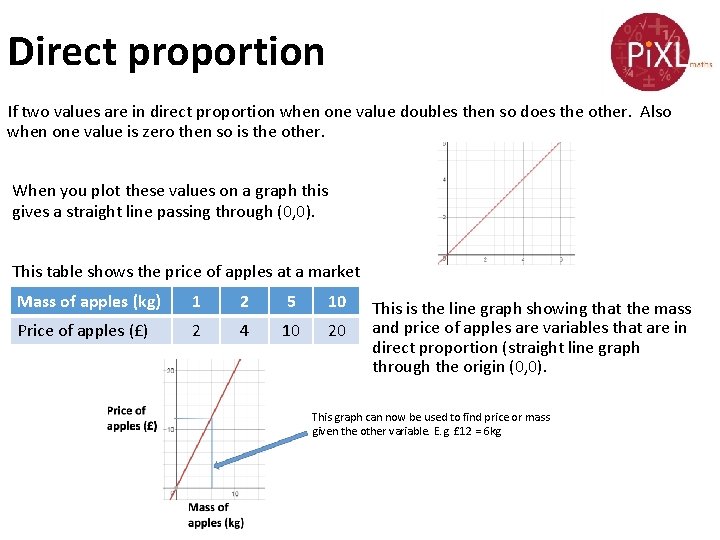
Direct proportion If two values are in direct proportion when one value doubles then so does the other. Also when one value is zero then so is the other. When you plot these values on a graph this gives a straight line passing through (0, 0). This table shows the price of apples at a market Mass of apples (kg) 1 2 5 10 Price of apples (£) 2 4 10 20 This is the line graph showing that the mass and price of apples are variables that are in direct proportion (straight line graph through the origin (0, 0). This graph can now be used to find price or mass given the other variable. E. g. £ 12 = 6 kg
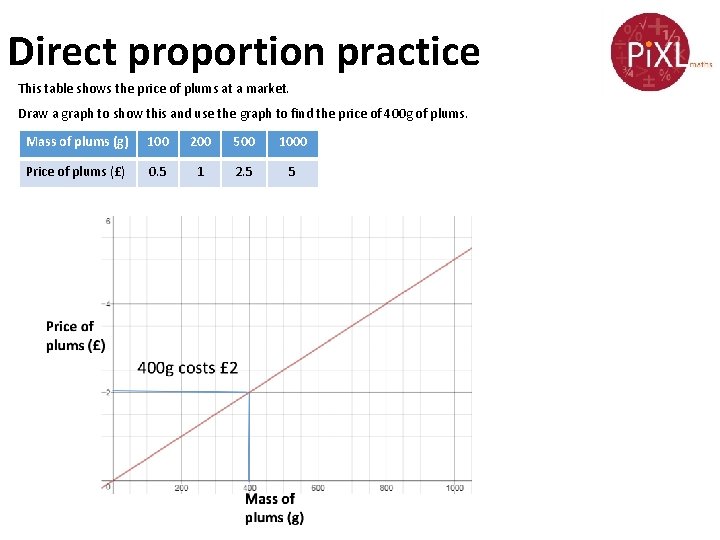
Direct proportion practice This table shows the price of plums at a market. Draw a graph to show this and use the graph to find the price of 400 g of plums. Mass of plums (g) 100 200 500 1000 Price of plums (£) 0. 5 1 2. 5 5
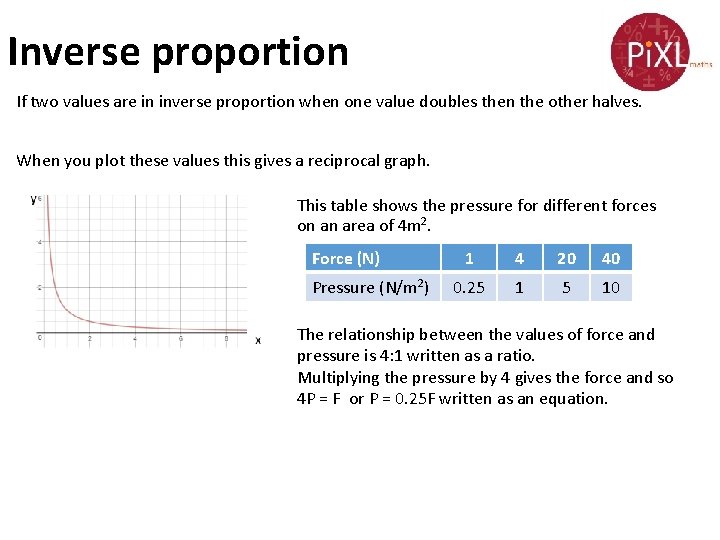
Inverse proportion If two values are in inverse proportion when one value doubles then the other halves. When you plot these values this gives a reciprocal graph. This table shows the pressure for different forces on an area of 4 m 2. Force (N) Pressure (N/m 2) 1 4 20 40 0. 25 1 5 10 The relationship between the values of force and pressure is 4: 1 written as a ratio. Multiplying the pressure by 4 gives the force and so 4 P = F or P = 0. 25 F written as an equation.

Inverse proportion practice Q 1: This table shows the relationship between two variables. x 1 2 10 20 y 0. 5 10 What is the relationship between the values of x and y written as a ratio. Write the relationship between x and y as an equation. The relationship between the values of x and y is 2: 1 written as a ratio. So 2 y = x or y = 0. 5 x written as an equation. Q 2: If it takes 5 builders 20 days to build a wall. How many days would it take 2 builders to build another wall the same size? 1 builder would take 20 x 5 = 100 days 2 builders would take 100 ÷ 2 = 50 days
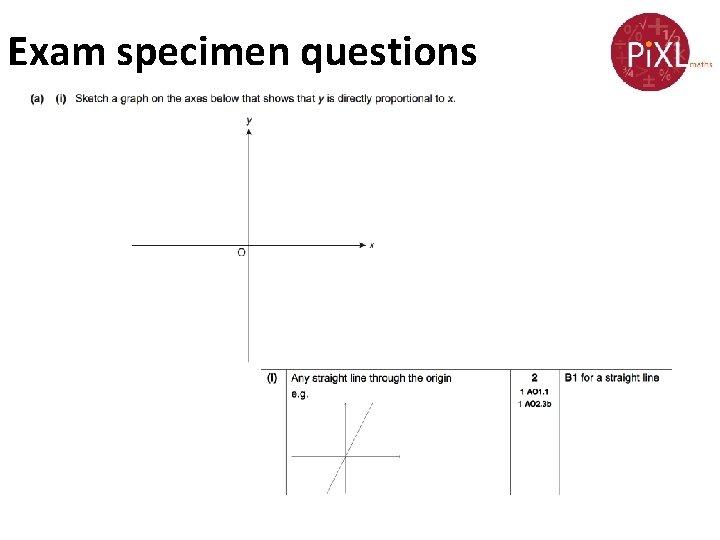
Exam specimen questions

Exam specimen questions

Exam specimen questions
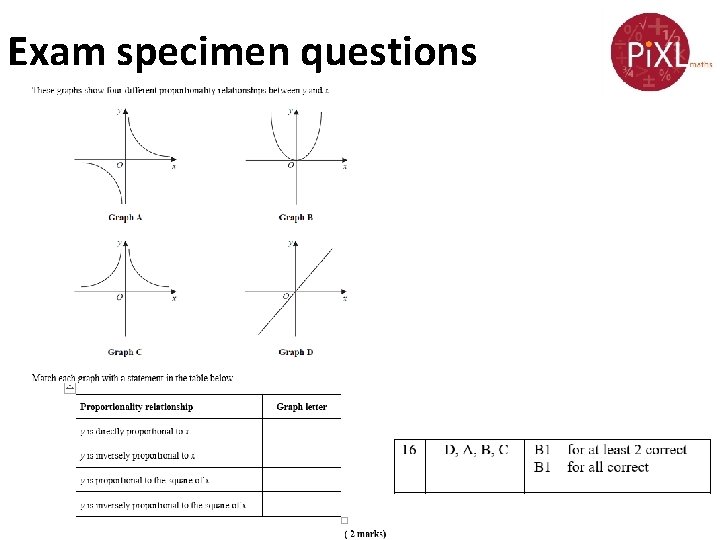
Exam specimen questions

Exam specimen questions

Exam specimen questions
- Slides: 12