Linear Inequalities Copy these key points into your





- Slides: 10

Linear Inequalities Copy these key points into your notes and then study for your quiz!! Key Terms: A Linear Inequality: involves a linear expression in two variables by using any of the relational symbols such as <, >, ≤ or ≥ Solutions of an Inequality: all points that make the inequality true These points are going to be revealed by a shaded area below or above a curve Dashed Lines: used for <, > (non-inclusive)

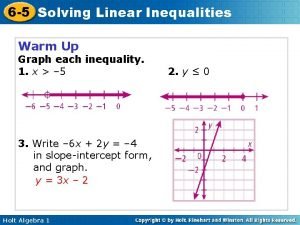
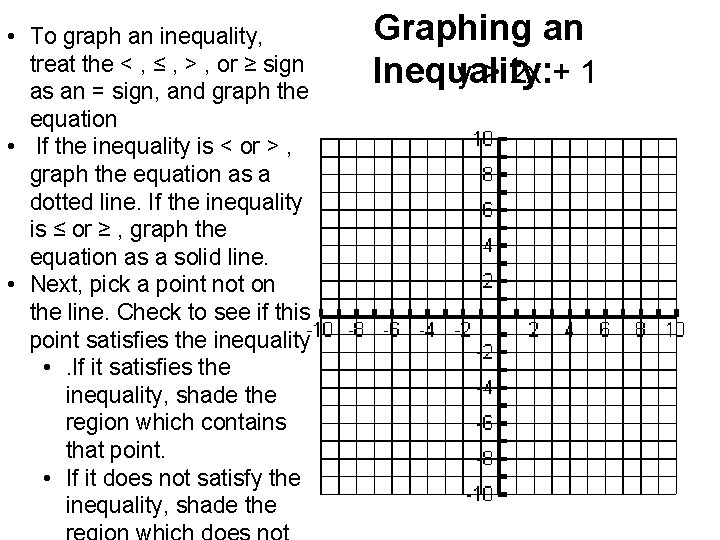
• To graph an inequality, treat the < , ≤ , > , or ≥ sign as an = sign, and graph the equation • If the inequality is < or > , graph the equation as a dotted line. If the inequality is ≤ or ≥ , graph the equation as a solid line. • Next, pick a point not on the line. Check to see if this point satisfies the inequality • . If it satisfies the inequality, shade the region which contains that point. • If it does not satisfy the inequality, shade the Graphing an Inequality: y > 2 x + 1

Let’s Put 2 and 2 Together! Systems + Graphing Inequities=Today! We should be able to: • Graph and inequality • Graph 2 inequalities on the same graph • Identify the shared region

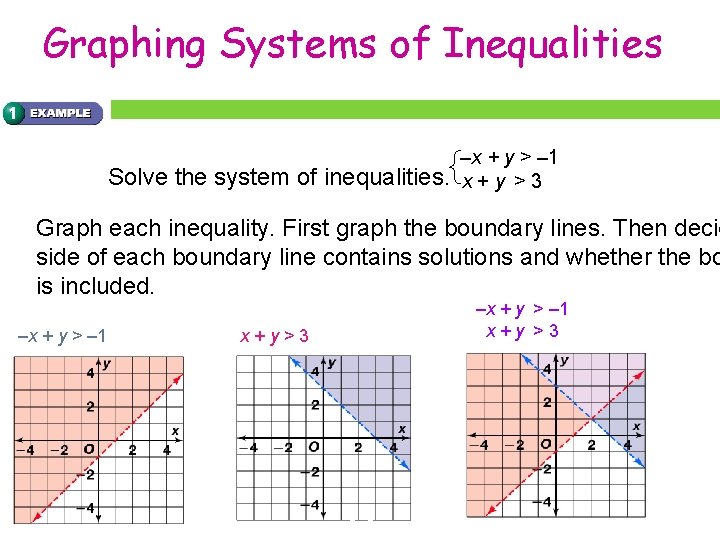
Graphing Systems of Inequalities Solve the system of inequalities. –x + y > – 1 x+y >3 Graph each inequality. First graph the boundary lines. Then decid side of each boundary line contains solutions and whether the bo is included. –x + y > – 1 x+y >3 x+y>3 3 -3

Systems of Inequalities (continued) Every point in the red region above the dashed line is a solution of Every point in the blue region above the dashed line is a solution o Every point in the purple region where the red and blue regions intersect is a solution of the system. For example (2, 2) is a solution. Check: Check (2, 2) in both inequalities of the system. –x + y > – 1 x+y >3 –(2) + (2) > – 1 (2) + (2) > 3 0 > – 1 4 >3

You Try Solve the following system: 2 x – 3 y < 12 x + 5 y < 20 x>0

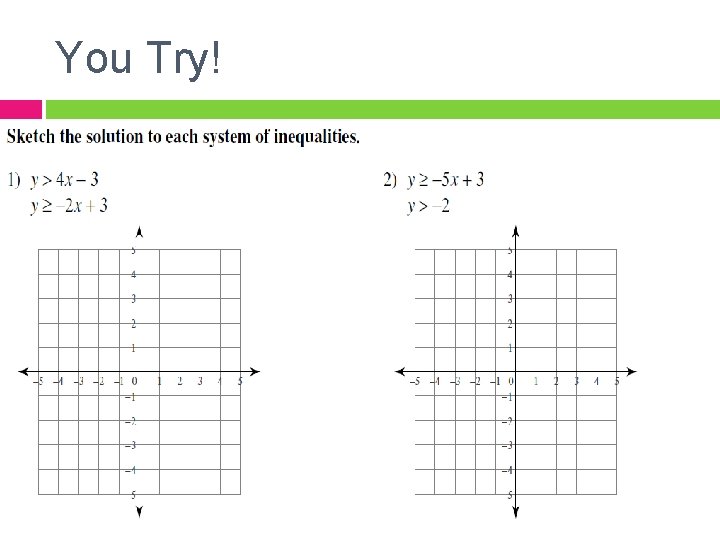
You Try!

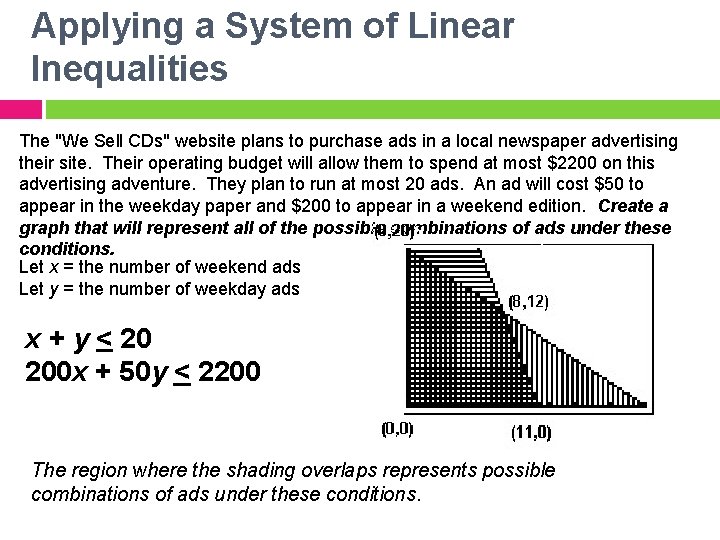
Applying a System of Linear Inequalities The "We Sell CDs" website plans to purchase ads in a local newspaper advertising their site. Their operating budget will allow them to spend at most $2200 on this advertising adventure. They plan to run at most 20 ads. An ad will cost $50 to appear in the weekday paper and $200 to appear in a weekend edition. Create a graph that will represent all of the possible combinations of ads under these conditions. Let x = the number of weekend ads Let y = the number of weekday ads x + y < 20 200 x + 50 y < 2200 The region where the shading overlaps represents possible combinations of ads under these conditions.

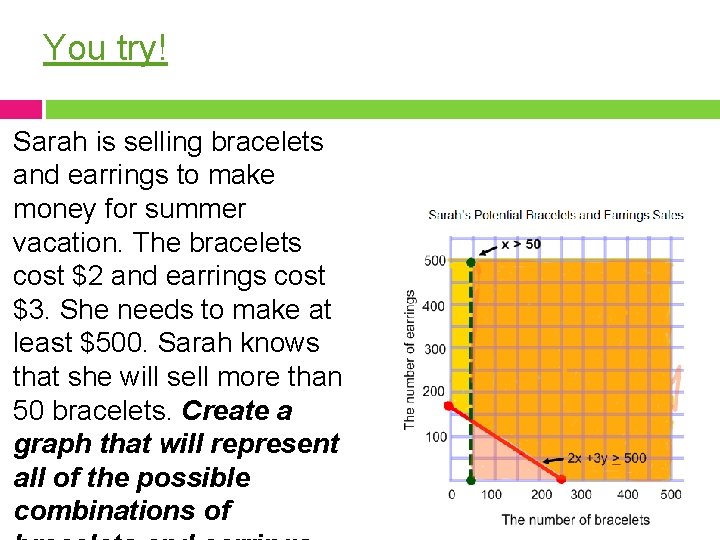
You try! Sarah is selling bracelets and earrings to make money for summer vacation. The bracelets cost $2 and earrings cost $3. She needs to make at least $500. Sarah knows that she will sell more than 50 bracelets. Create a graph that will represent all of the possible combinations of

Exit Ticket! (Be precise in your graphing ) Graph the following precisely! 1) 3) 2) 4) Which of the following ordered pairs is part of the solution to the following system of inequalities? a) (0, 0) b) (5, 0) c) (-4, 3)
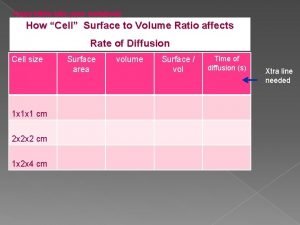
 Complete the table by copying it in your notebook.
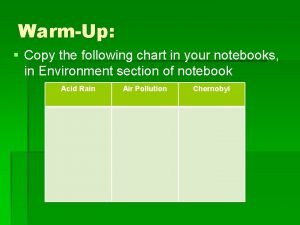
Complete the table by copying it in your notebook. Copy the world map in your notebook
Copy the world map in your notebook Copy in your notebook
Copy in your notebook Copy in your notebook
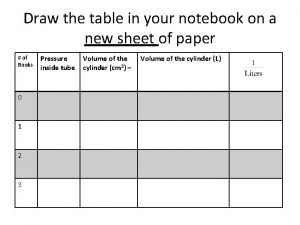
Copy in your notebook Draw the table in your notebook
Draw the table in your notebook 6-5 linear inequalities answer key
6-5 linear inequalities answer key 6-5 linear inequalities
6-5 linear inequalities Inequality graph examples
Inequality graph examples 6-5 linear inequalities answer key
6-5 linear inequalities answer key Trigonometric functions maze
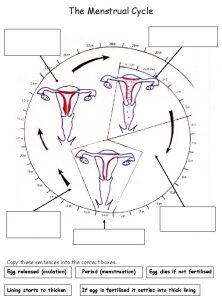
Trigonometric functions maze Copy these sentences to the correct boxes below
Copy these sentences to the correct boxes below