Lecture 6 Standing waves on a stretched string

Lecture 6 - Standing waves on a stretched string. D Aims: ë Semi-infinite string: >Standing waves arising from reflection: >counter-propagating waves. ë String of finite length: >Quantisation; >violins and laser cavities. ë 2 -D and 3 -D standing waves. >Rectangular, elastic sheet; >Waves in a box (black-body radiation). 1 Waves 6

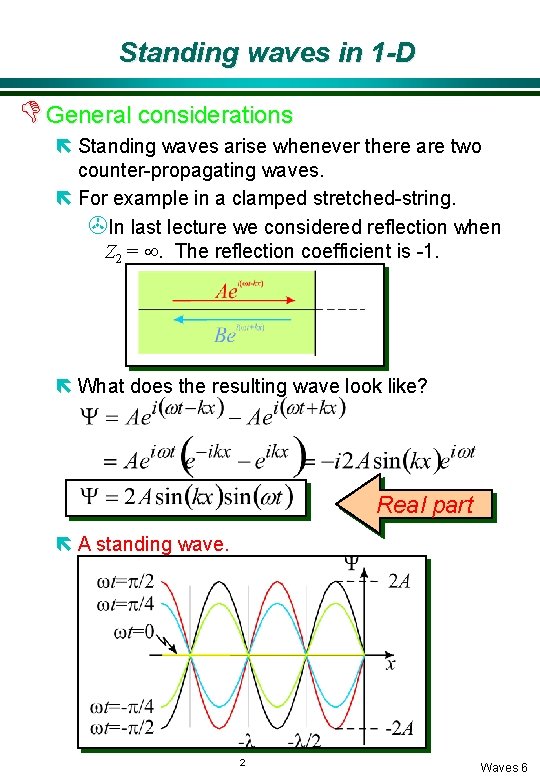
Standing waves in 1 -D D General considerations ë Standing waves arise whenever there are two counter-propagating waves. ë For example in a clamped stretched-string. >In last lecture we considered reflection when Z 2 = ¥. The reflection coefficient is -1. ë What does the resulting wave look like? Real part ë A standing wave. 2 Waves 6

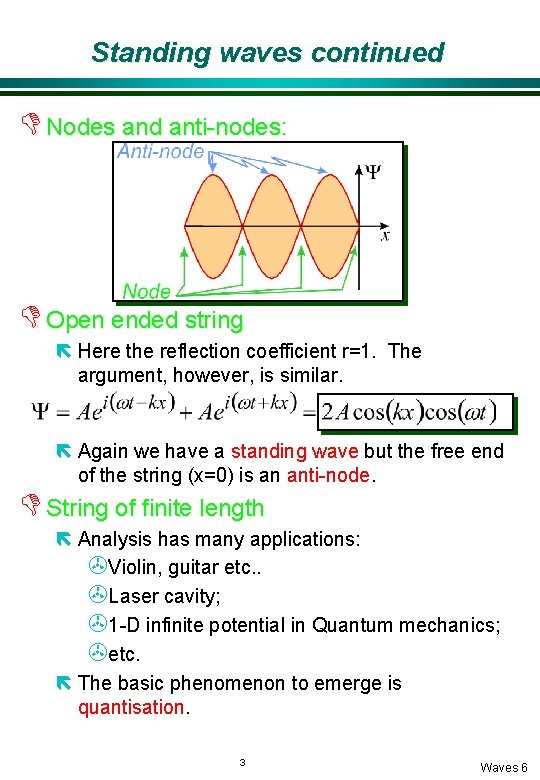
Standing waves continued D Nodes and anti-nodes: D Open ended string ë Here the reflection coefficient r=1. The argument, however, is similar. ë Again we have a standing wave but the free end of the string (x=0) is an anti-node. D String of finite length ë Analysis has many applications: >Violin, guitar etc. . >Laser cavity; >1 -D infinite potential in Quantum mechanics; >etc. ë The basic phenomenon to emerge is quantisation. 3 Waves 6

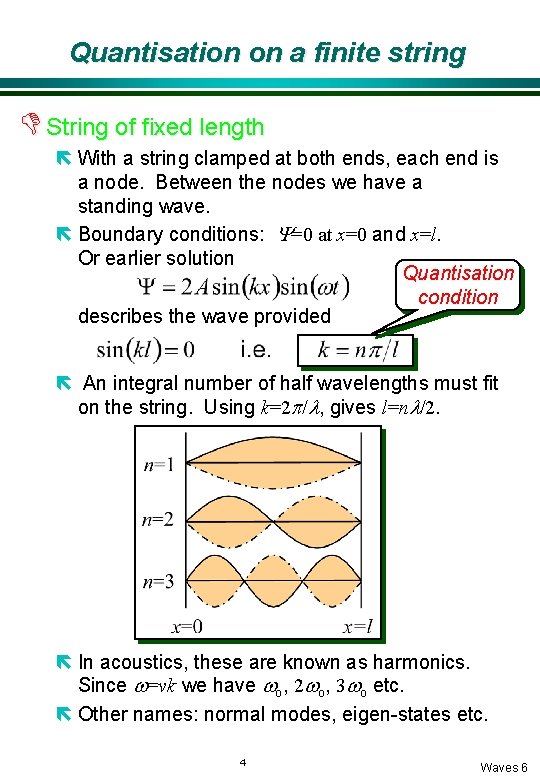
Quantisation on a finite string D String of fixed length ë With a string clamped at both ends, each end is a node. Between the nodes we have a standing wave. ë Boundary conditions: Y=0 at x=0 and x=l. Or earlier solution Quantisation condition describes the wave provided ë An integral number of half wavelengths must fit on the string. Using k=2 p/l, gives l=nl/2. ë In acoustics, these are known as harmonics. Since w=vk we have wo, 2 wo, 3 wo etc. ë Other names: normal modes, eigen-states etc. 4 Waves 6

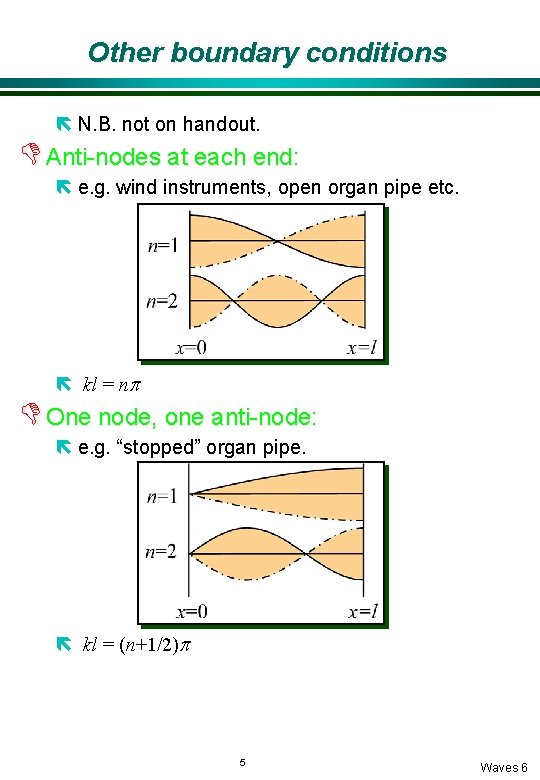
Other boundary conditions ë N. B. not on handout. D Anti-nodes at each end: ë e. g. wind instruments, open organ pipe etc. ë kl = np D One node, one anti-node: ë e. g. “stopped” organ pipe. ë kl = (n+1/2)p 5 Waves 6

Standing waves in 2 - and 3 -D D Examples: ë acoustics of drums, soundboards etc. ë electron states in 2 -D and 3 -D potential wells ë black-body radiation (photons in a cavity) ë phonon modes in solids (will be used in “Thermal Physics” to describe the Debye theory for thermal capacity of a solid) D 2 -D standing waves on a rectangular sheet: ë Boundary x=0, a; and y=0, b. z 2=¥ outside. ë Reflection at each boundary results in a phase change of p. Thus, Superposition gives 6 Waves 6

2 -D standing wave solution D Boundary conditions ë Must have: Y=0 at x=0, a; and y=0, b. Quantisation conditions ë Each pair of integers, (nx, ny), specifies a normal mode. ë Frequency of vibration follows from 7 Waves 6

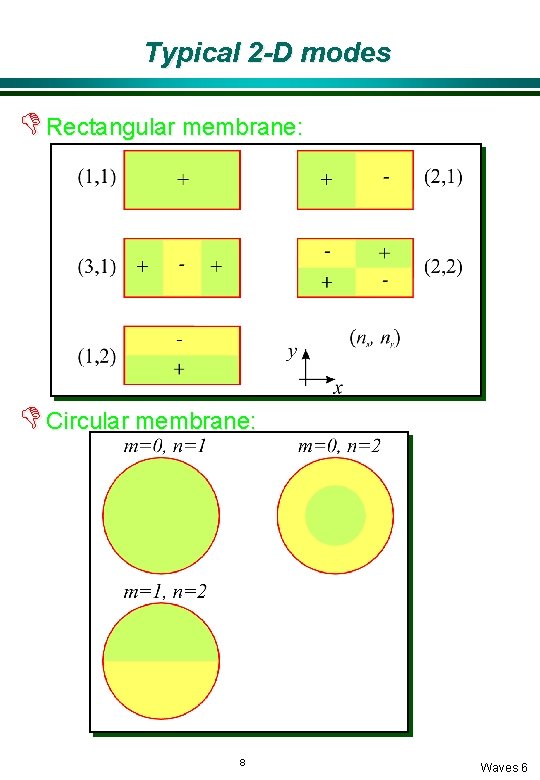
Typical 2 -D modes D Rectangular membrane: D Circular membrane: 8 Waves 6

3 -D: stabding waves in a box D Extend argument to 3 -D ë ë boundary conditions lead to quantisation conditions: ë Thus, gives the frequency of the normal modes as: 9 Waves 6