Lecture 4 Stretched string Transverse waves on a

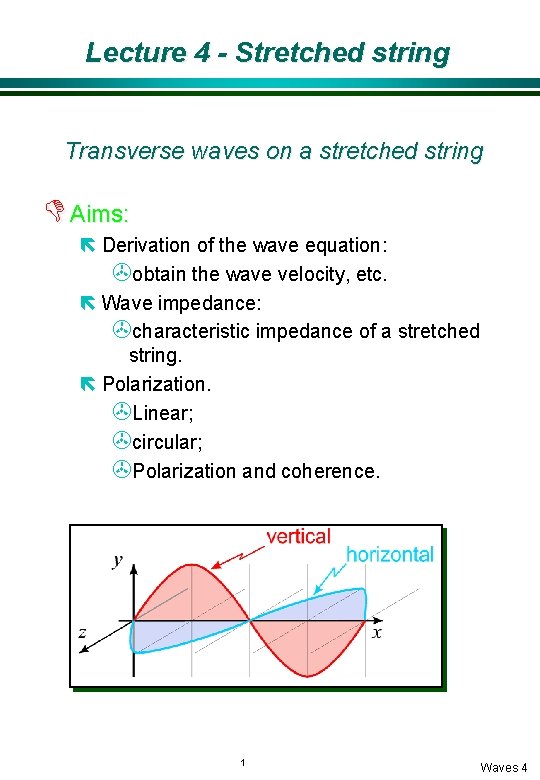
Lecture 4 - Stretched string Transverse waves on a stretched string D Aims: ë Derivation of the wave equation: >obtain the wave velocity, etc. ë Wave impedance: >characteristic impedance of a stretched string. ë Polarization. >Linear; >circular; >Polarization and coherence. 1 Waves 4

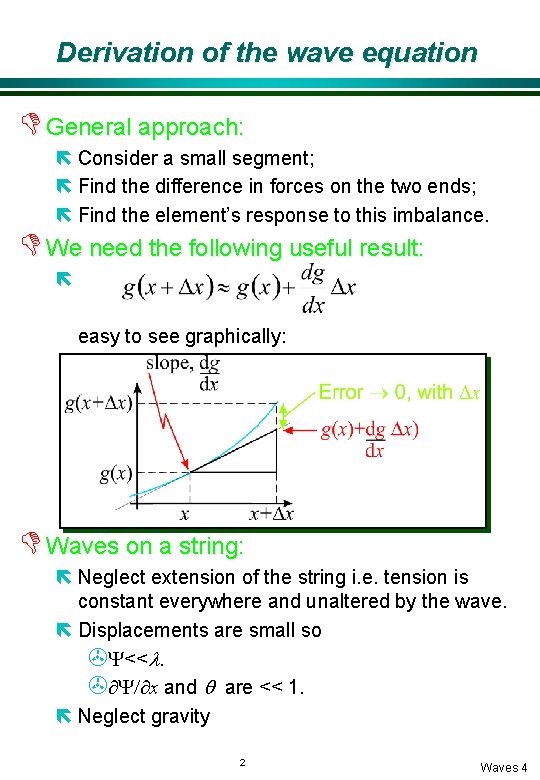
Derivation of the wave equation D General approach: ë Consider a small segment; ë Find the difference in forces on the two ends; ë Find the element’s response to this imbalance. D We need the following useful result: ë easy to see graphically: D Waves on a string: ë Neglect extension of the string i. e. tension is constant everywhere and unaltered by the wave. ë Displacements are small so >Y<<l. >¶Y/¶x and q are << 1. ë Neglect gravity 2 Waves 4

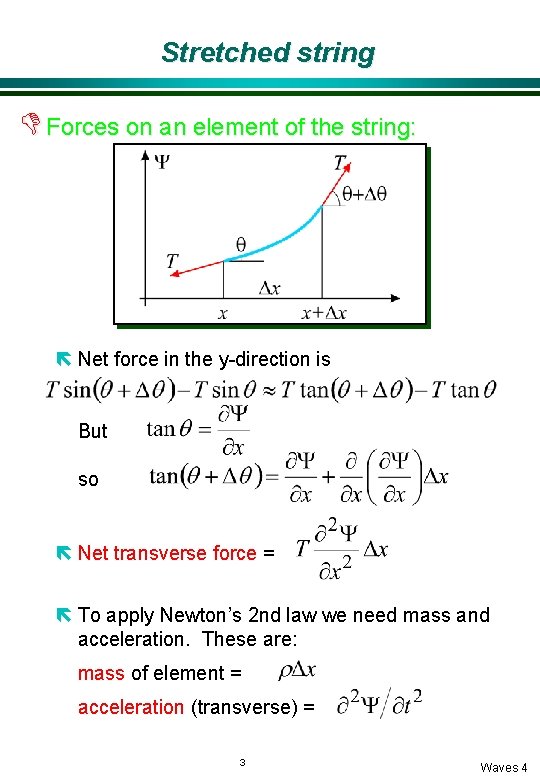
Stretched string D Forces on an element of the string: ë Net force in the y-direction is But so ë Net transverse force = ë To apply Newton’s 2 nd law we need mass and acceleration. These are: mass of element = acceleration (transverse) = 3 Waves 4

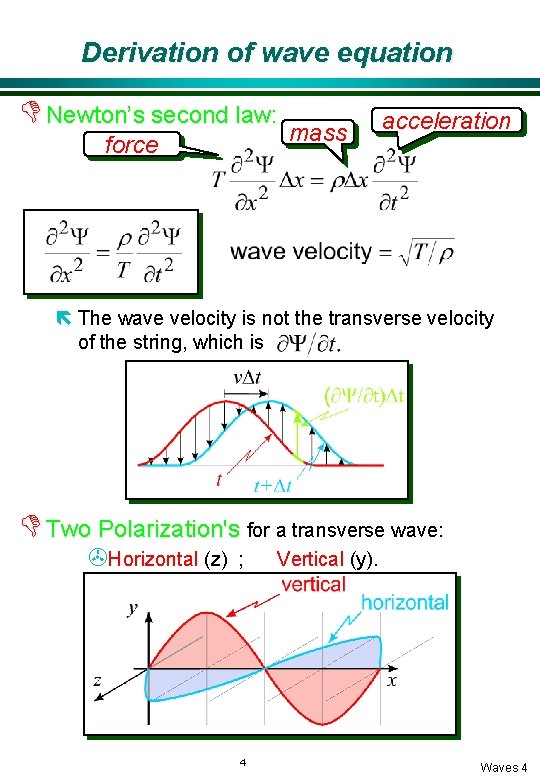
Derivation of wave equation D Newton’s second law: mass force acceleration ë The wave velocity is not the transverse velocity of the string, which is D Two Polarization's for a transverse wave: >Horizontal (z) ; 4 Vertical (y). Waves 4

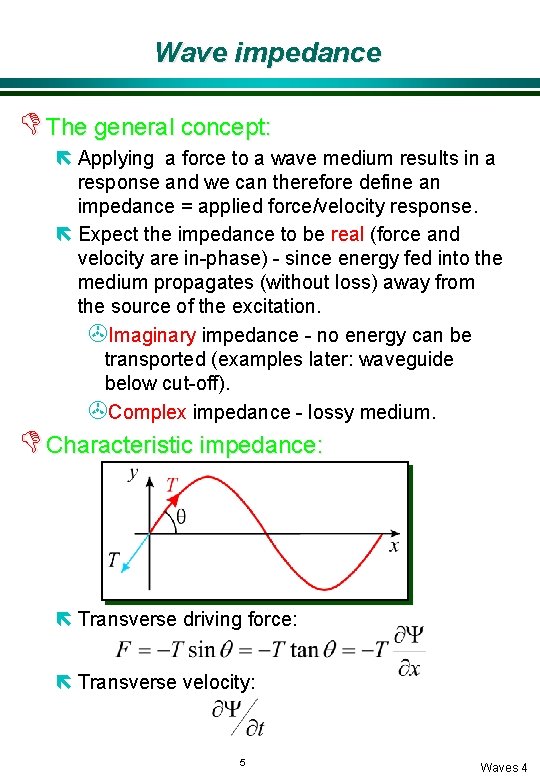
Wave impedance D The general concept: ë Applying a force to a wave medium results in a response and we can therefore define an impedance = applied force/velocity response. ë Expect the impedance to be real (force and velocity are in-phase) - since energy fed into the medium propagates (without loss) away from the source of the excitation. >Imaginary impedance - no energy can be transported (examples later: waveguide below cut-off). >Complex impedance - lossy medium. D Characteristic impedance: ë Transverse driving force: ë Transverse velocity: 5 Waves 4

Impedance of a stretched string D Impedance ë ë For a wave in +ve x-direction, recall ë Impedance (for wave in +ve x-direction) ë Wave in -ve x-direction, Z has the opposite sign: ë Note that the impedance is real. i. e. the medium is lossless (in this idealised picture). 6 Waves 4

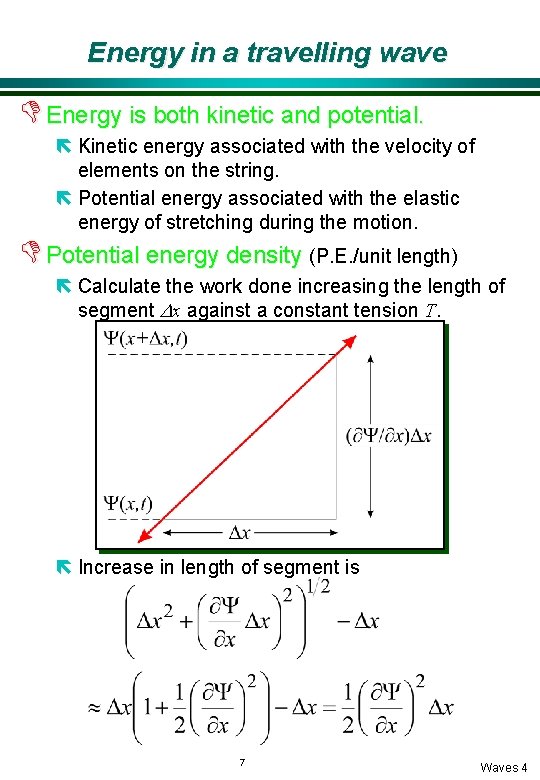
Energy in a travelling wave D Energy is both kinetic and potential. ë Kinetic energy associated with the velocity of elements on the string. ë Potential energy associated with the elastic energy of stretching during the motion. D Potential energy density (P. E. /unit length) ë Calculate the work done increasing the length of segment Dx against a constant tension T. ë Increase in length of segment is 7 Waves 4

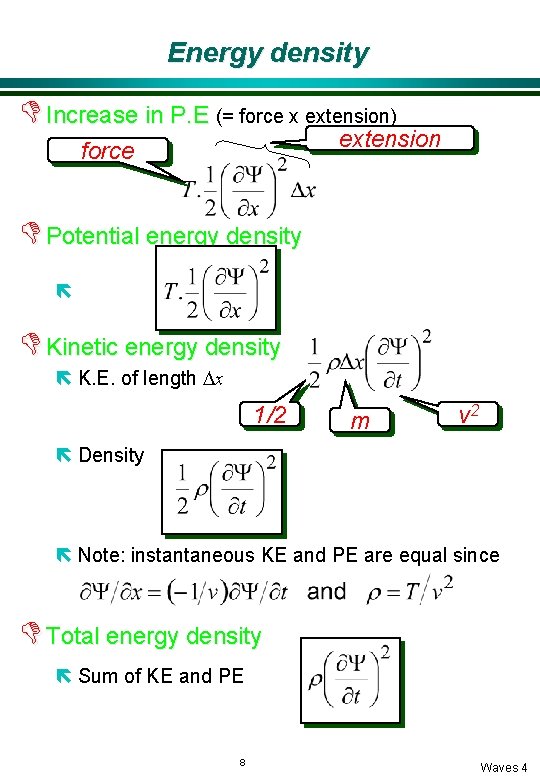
Energy density D Increase in P. E (= force x extension) extension force D Potential energy density ë D Kinetic energy density ë K. E. of length Dx 1/2 m v 2 ë Density ë Note: instantaneous KE and PE are equal since D Total energy density ë Sum of KE and PE 8 Waves 4

Energy: harmonic wave D Average energy density (section 1. 1. 3) ë ë average energy density is ë consider each element, length Dx, as an oscillator with energy ë In time Dt we excite a length Dx=v. Dt. So the energy input is ë Since Z=rv, D Mean power 9 Waves 4