IMMANUEL KANT RUSSIAN STATE UNIVERSITY ZIRCONIUM DIBORIDE SHOCK

IMMANUEL KANT RUSSIAN STATE UNIVERSITY ZIRCONIUM DIBORIDE SHOCK SYNTHESIS V. N. Leitsin, M. A. Dmitrieva, I. V. Kobral

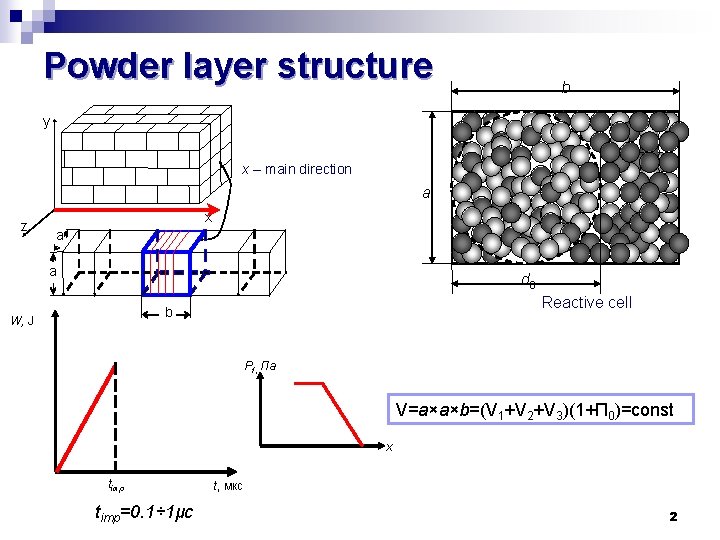
Powder layer structure b y x – main direction a z x a a d 0 Reactive cell b W, J Pf, Па V=a×a×b=(V 1+V 2+V 3)(1+П 0)=const x timp=0. 1÷ 1μc t, мкс 2

Computer Simulation Concept State parameters of powder medium behind shock pulse front 3

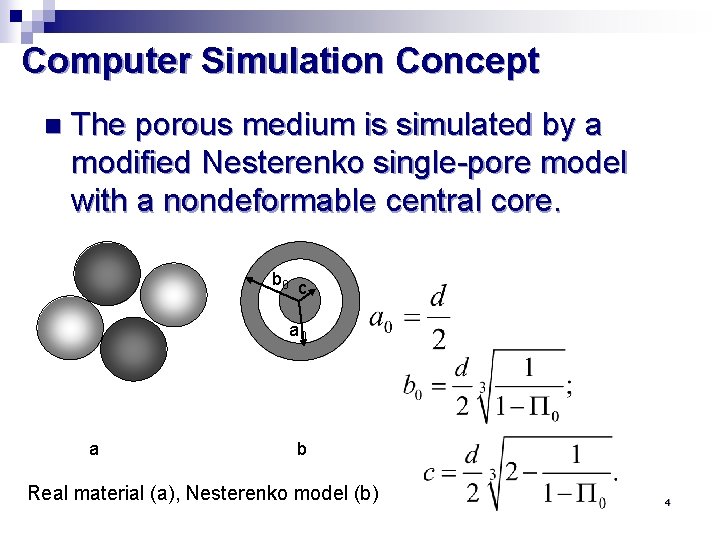
Computer Simulation Concept n The porous medium is simulated by a modified Nesterenko single-pore model with a nondeformable central core. b 0 c а 0 а b Real material (а), Nesterenko model (b) 4

Computer Simulation Concept n specific energy, WD, dissipating in the surroundings of a pore at the collapse stage nat further stages, energy is expended to disrupt the boundary layers of particles implementing non-stationary compacting mode mechanisms Wk=W-WD 5

Computer Simulation Concept n The mechanical loading of powder mixture can increase the reactionary ability of reactive components 1. Plastic deformation: 2. Fracture of surface layers: 6

Computer Simulation Concept The law of conservation of energy 7

Computer Simulation Concept Volumetric heat transfer coefficient Skeleton thermal conductivity Heat sources: Heat losses: m =0, 7 мкс 8

Computer Simulation Concept n The exothermal conversion macrokinetics is supposed to be a multilevel reactionary cell model coordinated with the power law of reactionary diffusion. The kinetic function φ(z)=0, 5 z-1 Pre-exponent Change in the reactivity Condition of reactive equivalence 9

Computer Simulation Concept Filtration of liquid phase obeys the Darcy law Permeability coefficient Viscosity of the melt 0 exp(Еμ /RT), Porous pressure 10

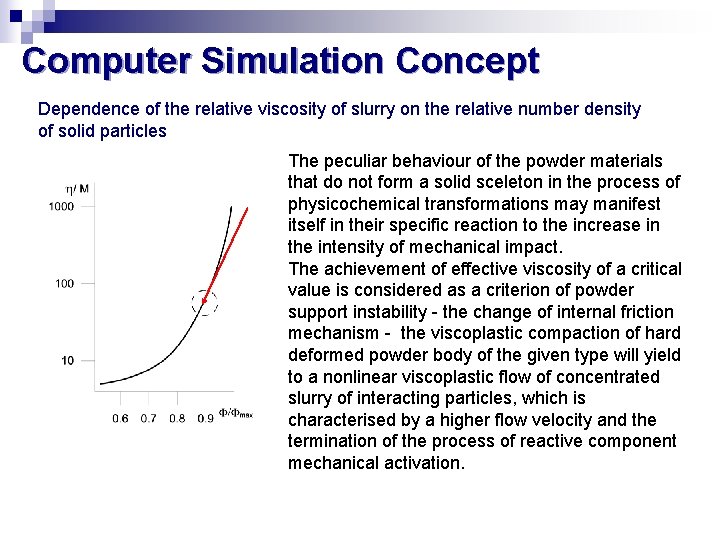
Computer Simulation Concept Dependence of the relative viscosity of slurry on the relative number density of solid particles The peculiar behaviour of the powder materials that do not form a solid sceleton in the process of physicochemical transformations may manifest itself in their specific reaction to the increase in the intensity of mechanical impact. The achievement of effective viscosity of a critical value is considered as a criterion of powder support instability - the change of internal friction mechanism - the viscoplastic compaction of hard deformed powder body of the given type will yield to a nonlinear viscoplastic flow of concentrated slurry of interacting particles, which is characterised by a higher flow velocity and the termination of the process of reactive component mechanical activation.

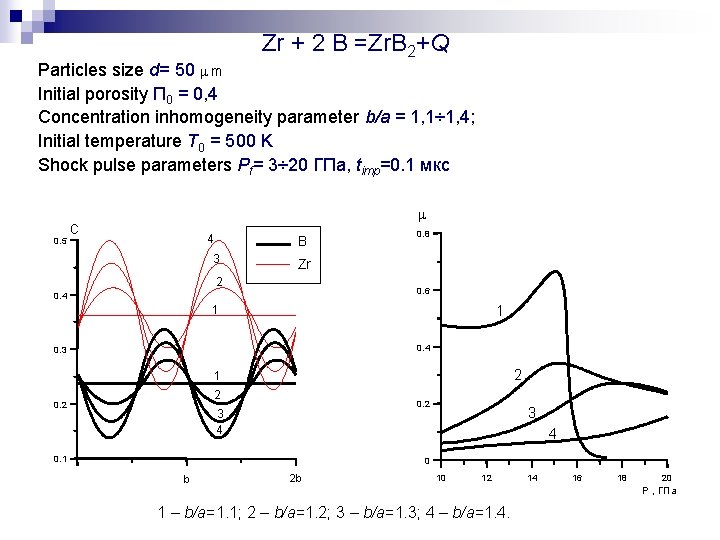
Zr + 2 B =Zr. B 2+Q Particles size d= 50 m m Initial porosity П 0 = 0, 4 Concentration inhomogeneity parameter b/a = 1, 1÷ 1, 4; Initial temperature T 0 = 500 K Shock pulse parameters Pf= 3÷ 20 ГПа, timp=0. 1 мкс 0. 5 m C 4 B 3 0. 8 Zr 2 0. 6 0. 4 1 1 0. 4 0. 3 2 1 2 0. 2 3 4 0. 1 0 b 2 b 10 12 14 16 18 20 Р , ГПа 1 – b/a=1. 1; 2 – b/a=1. 2; 3 – b/a=1. 3; 4 – b/a=1. 4.

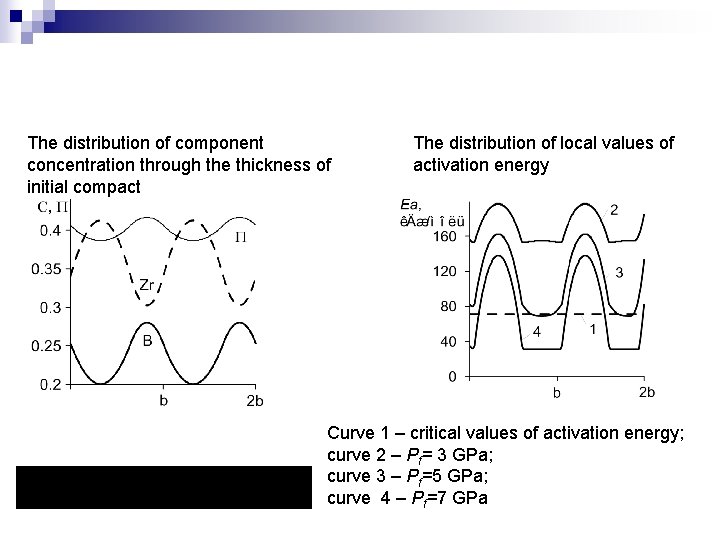
The distribution of component concentration through the thickness of initial compact The distribution of local values of activation energy Curve 1 – critical values of activation energy; curve 2 – Pf= 3 GPa; curve 3 – Pf=5 GPa; curve 4 – Pf=7 GPa

Conclusion n n The data presented suggest that the degree of mechanical activation of Zr-B mixture reactive components play the key role in the satisfaction of the conditions of shock initiation of chemical transformations. For the macroscopically heterogeneous powder mixture, shock initiation is possible in the areas with an excess of refractory component. The change of internal friction mechanism is key feature of zirconium diboride shock synthesis Thank You for Your attention 14