IL TRIANGOLO DI TARTAGLIA 1500 1557 Il nome

IL TRIANGOLO DI TARTAGLIA

1500 - 1557

Il nome di tartaglia è noto per il triangolo che porta il suo nome. Eppure il triangolo non fu un’opera interamente sua , di fatti , molti uomini orientali contribuirono alla nascita di questo elemento. Anche Newton lo ripropose in modo completamente nuovo , nei suoi studi sul calcolo della probabilità. Il famoso Leonardo Fibonacci , può essere considerato il predecessore dell’idea di Tartaglia. Infatti anche nel suo libro liber abaci , descrive , in un certo qual modo , questa innovazione. Per poter capire come i due matematici siano legati , occorre far riferimento ad uno dei problemi di Fibonacci.

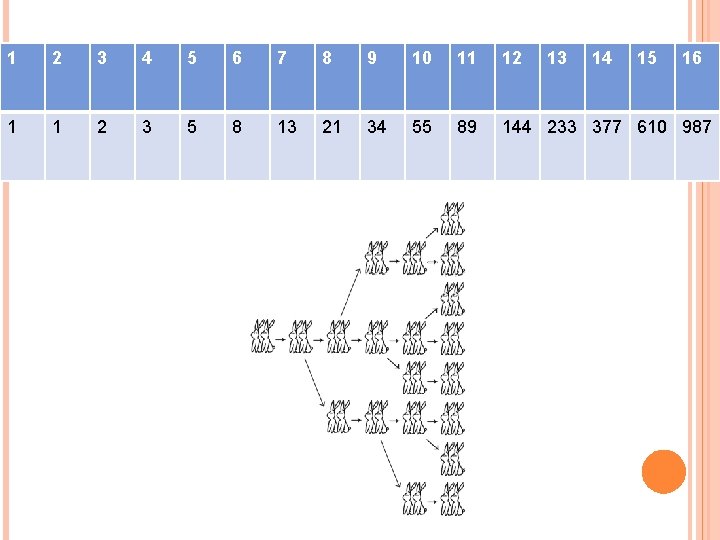
Due conigli , i quali riescono a procreare solamente nel mese di Gennaio , danno alla luce due figli nel mese di Febbraio e a loro volta questi ultimi , diventati grandi procreeranno altri due figli dopo due mesi da quando hanno la possibilità di svolgere quest’ azione. Fibonacci , contando le coppie presenti ogni mese , ottenne una sequenza di numeri che porta il suo nome : 1 , 2 , 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Nel giro di un anno , la coppia di conigli ha generato altre 232 coppie di conigli. La serie funziona in questo modo, a partire dal 3 numero ciascuno dei successivi corrisponde alla somma dei 2 precedenti

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987

Ma la nuova seria ha anche altre proprietà : -Sommando i primi numeri e aggiungendone 1 alla somma , si ottiene il numero di posto numero 2 -Tenendo sempre il primo numero e sommando i numeri della seria , prendendone uno si e uno no , fermandosi all’ennesimo si ottiene il numero di posto numero +1 - Facendo il quadrato del numero di posto K e sommando al quadrato del numero di posto K +1 , si ottiene il numero di posto 2 k +1 -Un qualsiasi numero della serie , di posto pari , elevato al quadrato è il prodotto di quello che lo precede e di quello che lo segue , meno uno ; un qualsiasi numero della serie di posto dispari , elevato al quadrato , è il prodotto di quello che lo precede

E di quello che lo precede ; Anche in natura possiamo riscontrare la presenza di molti schemi di Fibonacci : -Molti fiori hanno un numero di petali pari ad un numero pari alla serie di Fibonacci ( crisantemo 13 petali , margherita 34 , 55 , 89 petali - La disposizione delle foglie , dei ramoscelli , degli steli , ovvero la fillotassi rispetto alla serie di Fibonacci -Le pigne numeri di Fibonacci hanno la tendenza di comparire come spirale Destrorse e sinistrorse e lo stesso avviene con i semi di girasole -L’ananas è un’ottima pianta in cui cercare i numeri di Fibonacci

Il triangolo di Tartaglia , apparentemente simile a quello di Fibonacci , si compone mettendo alla sommità il numero 1, nella riga successiva una coppia di 1 e per le righe successive si procede ponendo all’inizio sempre 1, mentre gli altri numeri si ottengono sommando via le coppie di numeri che li precedono e li seguono nella riga superiore. Si può così continuare all’infinito. o utilizzò per trovare i coefficienti dell’elevamento a potenza di un binomio. Per ottenerne il quadrato, per esempio, bisogna moltiplicare il binomio (a+b) per se stesso: il risultato è a 2+ 2 ab+b 2. I numeri che precedono le lettere corrispondono proprio a quelli della seconda riga del triangolo di Tartaglia.

Il filosofo e matematico francese Blaise Pascal (16231662) utilizzò invece il triangolo per ricavare tutti gli abbinamenti possibili tra alcuni gruppi di numeri predefiniti. Se, per esempio, si vuole scoprire quante sono le strette di mano che si possono scambiare 2, 4 o 10 persone diverse, bisogna andare nella riga del 2 del triangolo e scorrere una delle due diagonali corrispondenti (sono uguali): accanto ai numeri ipotizzati, si trova il risultato: tra 2 persone è possibile una sola stretta di mano, tra 4 sono possibili 6 strette, tra 10 sono possibili 45 strette di mano.

Realizzato da : Lena Signoretta Gustavo Pregoni IV GINNASIO