Formuls gylis Prefiksinis postfiksinis ir infiksinis pavidalai Rekursinis





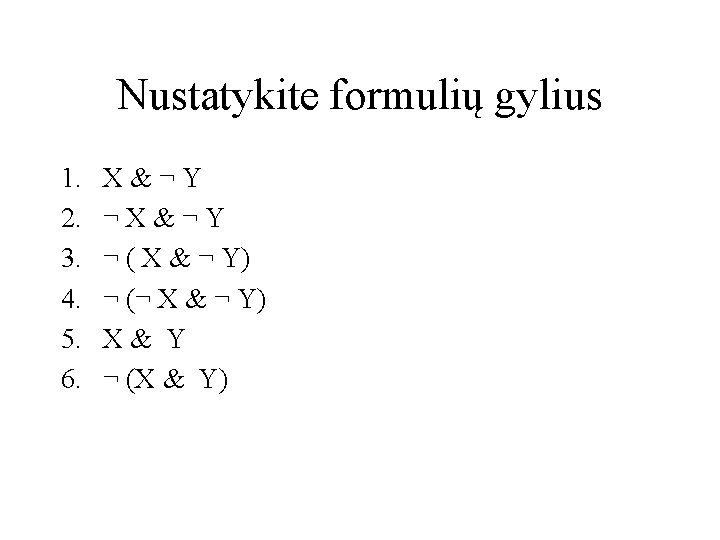
















- Slides: 22

Formulės gylis. Prefiksinis, postfiksinis ir infiksinis pavidalai

Rekursinis formulių aibės apibrėžimas F 0 = a, b, …, A, B, …, x 1, …, Y 2, …; Fn+1 = Fn U {(¬ x): x Fn} U {(x & y): x, y Fn} U {( x v y ): x, y Fn} U {(x y): x, y Fn} U {( x y): x, y Fn} U … Formulės F gyliu vadinamas skaičius

Raskite formulės gylį: ((( e v t ) ¬ s) | ( ¬ t & u )) v ( s ( e | u )) Loginiai kintamieji yra nulinio gylio formulės. Šiuo atveju kintamieji yra e, t, s, u. Nulinio gylio formules žymėsime A 0. Tada formulę galima perrašyti taip: ((( A 0 v A 0 ) ¬ A 0) | ( ¬ A 0 & A 0 )) v ( A 0 | A 0 )) Atlikus vieną veiksmą su dviem nulinio gylio formulėmis arba neigimą su nulinio gylio formulę, gausime pirmo gylio formulę. Jas žymėsime A 1. Šiuo atveju pirmo gylio formulės yra ( A 0 v A 0 ) ¬ A 0 ( A 0 | A 0 )

Perrašome formulę: ((( A 0 v A 0 ) ¬ A 0) | ( ¬ A 0 & A 0 )) v ( A 0 | A 0 )) (( A 1) | ( A 1 & A 0 )) v ( A 0 A 1) Paneigus pirmo gylio formulę ar atlikus vieną veiksmą su dviem pirmo ir nedidesnio už pirmą gylio formulėmis gauname antro gylio formulę. Šiuo atveju tai butu ( A 1) ( A 1 & A 0 ) Taigi gauname: ( A 2 | A 2 ) v A 2 ( A 0 A 1)

( A 2 | A 2 ) v A 2 Paneigus antro gylio formulę ar atlikus vieną veiksmą su dviem antro ir nedidesnio už antrą gylio formulėmis gauname trečio gylio formulę. Šiuo atveju tai butu ( A 2 | A 2 ) Tuomet gauname: A 3 v A 2 Rezultatas – ketvirto gylio formulė A 4
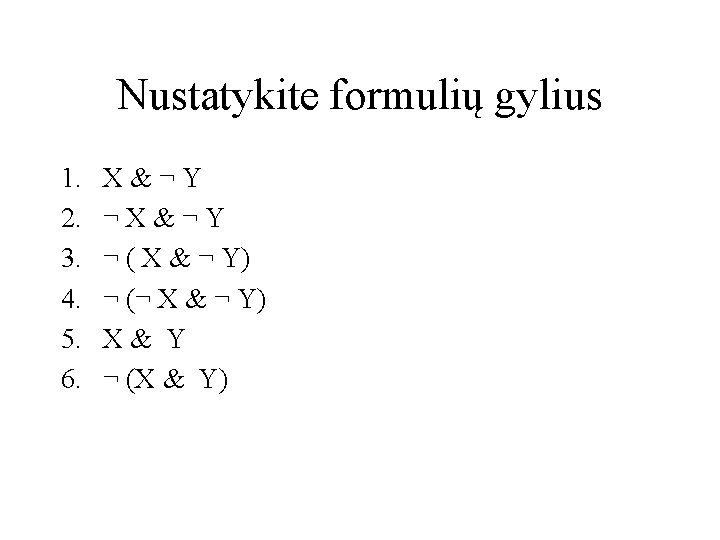
Nustatykite formulių gylius 1. 2. 3. 4. 5. 6. X&¬Y ¬ ( X & ¬ Y) ¬ (¬ X & ¬ Y) X& Y ¬ (X & Y)

Formulių užrašymo pavidalai 1. Infiksinis (tradicinis su skliaustais) A B 2. Prefiksinis (operacija operandai) AB 3. Postfiksinis (operandai operacija) AB

Perrašykite prefiksiniu pavidalu: ((( e v t ) ¬ s) | ( ¬ t & u )) v ( s ( e | u )) Randame visas pirmo gylio formules ir pažymime jas: A = ( e v t ); B = ¬ s; C= ¬t; D=(e|u) Prefiksiniu pavidalu jos atrodys taip: A=v et; B = ¬ s; C= ¬t; Pasinaudojame naujais žymėjimais: ((A B) | (C & u )) v ( s D) D=|eu

Randame pirmo gylio formules: ((A B) | (C & u )) v ( s D) E = (A B); F = (C & u ); G = ( s D) Prefiksiniu pavidalu jos atrodys taip: E = A B; F=&Cu; Pasinaudojame naujais žymėjimais: (E|F)v. G G= s. D

Tęsiame: (E|F)v. G I = E | F, prefiksiniu pavidalu: I = | E F Perrašome formulę J = I v G, Iv. G prefiksiniu pavidalu: J = v I G

Antras etapas – atbulinė eiga: J = v I G, kur I = | E F, G= s. D J=v|EF s. D, čia E = A B, F=&Cu, J=v| AB&Cu s|eu, čia A=v et, B = ¬ s, C= ¬t J=v| v et¬s&¬tu s|eu, D=|eu

Perrašyti infiksiniu pavidalu V| Vhz¬a&¬z¬x a|h x za Randame struktūras “operacija kintamasis” ir perrašome jas infiksiniu pavidalu. Prieš kintamąjį gali būti neigimas. A = V h z, t. y. A = h V z, B = & ¬ z ¬ x, B = ¬ z & ¬ x, Perrašome formulę: V| A¬a. B a|h x. C C = z a, C = z a.

Tą patį darysime su gauta formule: V| A¬a. B a|h x. C D = A ¬ a, t. y. E= x. C D = A ¬ a, Įrašome D ir E: V|DB a|h. E Tada F = | D B, G = | h E, t. y. F = D | B, G = h | E. E=x C

Perrašome: VF a. G Tada I = a G, ir I = a G. Formulė pertvarkoma: V F I, arba infiksiniu pavidalu F V I.

Atbulinė eiga (dabar prireiks skliaustų): F V I, kur F = D | B, I = a G. Įrašome: čia Įrašome: ( D | B ) V ( a G ), D = A ¬ a, B = ¬ z & ¬ x, G = h | E. (( A ¬ a ) | (¬ z & ¬ x ) ) V ( a ( h | E ) ).


Užduotys savarankiškam darbui










