Engineering Electromagnetics Lecture 6 Dr Ing Erwin Sitompul

Engineering Electromagnetics Lecture 6 Dr. -Ing. Erwin Sitompul President University http: //zitompul. wordpress. com 2 0 1 6 President University Erwin Sitompul EEM 6/1

Chapter 4 Energy and Potential The Potential Field of a System of Charges: Conservative Property n We will now prove, that for a system of charges, the potential is also independent of the path taken. n Continuing the discussion, the potential field at the point r due to a single point charge Q 1 located at r 1 is given by: n The field is linear with respect to charge so that superposition is applicable. Thus, the potential arising from n point charges is: President University Erwin Sitompul EEM 6/2

Chapter 4 Energy and Potential The Potential Field of a System of Charges: Conservative Property n If each point charge is now represented as a small element of continuous volume charge distribution ρvΔv, then: n As the number of elements approach infinity, we obtain the integral expression: n If the charge distribution takes from of a line charge or a surface charge, President University Erwin Sitompul EEM 6/3

Chapter 4 Energy and Potential The Potential Field of a System of Charges: Conservative Property n As illustration, let us find V on the z axis for a uniform line charge ρL in the form of a ring, ρ = a, in the z = 0 plane. • The potential arising from point charges or continuous charge distribution can be seen as the summation of potential arising from each charge or each differential charge. • It is independent of the path chosen. President University Erwin Sitompul EEM 6/4

Chapter 4 Energy and Potential The Potential Field of a System of Charges: Conservative Property n With zero reference at ∞, the expression for potential can be taken generally as: n Or, for potential difference: n Both expressions above are not dependent on the path chosen for the line integral, regardless of the source of the E field. • Potential conservation in a simple dc-circuit problem in the form of Kirchhoff’s voltage law n For static fields, no work is done in carrying the unit charge around any closed path. President University Erwin Sitompul EEM 6/5

Chapter 4 Energy and Potential Gradient n We have discussed two methods of determining potential: directly from the electric field intensity by means of a line integral, or from the basic charge distribution itself by a volume integral. n E or ρv known V asked n In practical problems, however, we rarely know E or ρv. n Preliminary information is much more likely to consist a description of two equipotential surface, and the goal is to find the electric field intensity. n V known E asked President University Erwin Sitompul EEM 6/6

Chapter 4 Energy and Potential Gradient n The general line-integral relationship between V and E is: n For a very short element of length ΔL, E is essentially constant: n Assuming a conservative field, for a given reference and starting point, the result of the integration is a function of the end point (x, y, z). We may pass to the limit and obtain: President University Erwin Sitompul EEM 6/7

Chapter 4 Energy and Potential Gradient n From the last equation, the maximum positive increment of potential, Δvmax, will occur when cosθ = – 1, or ΔL points in the direction opposite to E. n We can now conclude two characteristics of the relationship between E and V at any point: 1. The magnitude of E is given by the maximum value of the rate of change of V with distance L. 2. This maximum value of V is obtained when the direction of the distance increment is opposite to E. President University Erwin Sitompul EEM 6/8

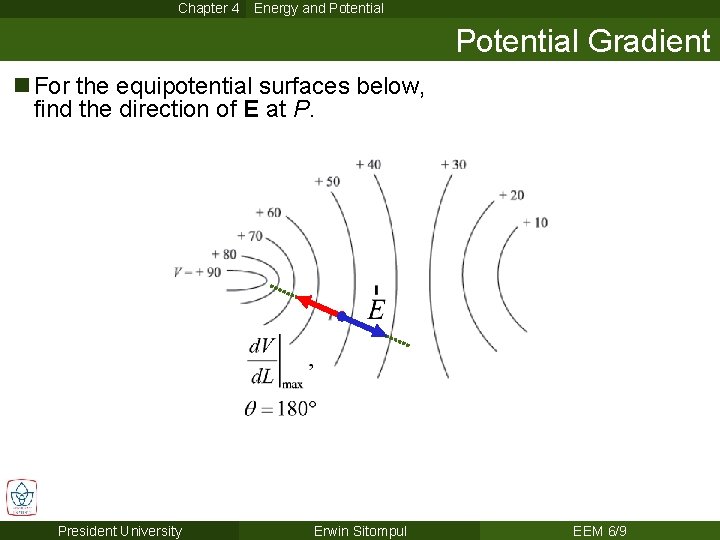
Chapter 4 Energy and Potential Gradient n For the equipotential surfaces below, find the direction of E at P. President University Erwin Sitompul EEM 6/9

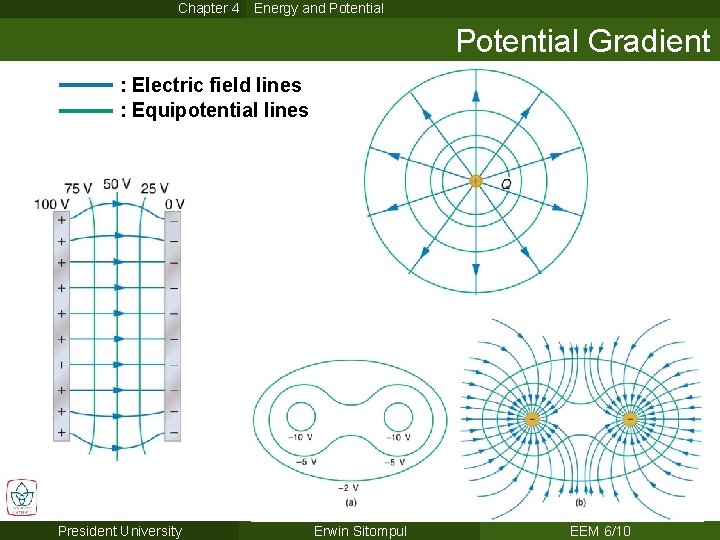
Chapter 4 Energy and Potential Gradient : Electric field lines : Equipotential lines President University Erwin Sitompul EEM 6/10

Chapter 4 Energy and Potential Gradient n Since the potential field information is more likely to be determined first, let us describe the direction of ΔL (which leads to a maximum increase in potential) in term of potential field. n Let a. N be a unit vector normal to the equipotential surface and directed toward the higher potential. n The electric field intensity is then expressed in terms of the potential as: n The maximum magnitude occurs when ΔL is in the a. N direction. Thus we define d. N as incremental length in a. N direction, President University Erwin Sitompul EEM 6/11

Chapter 4 Energy and Potential Gradient n We know that the mathematical operation to find the rate of change in a certain direction is called gradient. n Now, the gradient of a scalar field T is defined as: n Using the new term, President University Erwin Sitompul EEM 6/12

Chapter 4 Energy and Potential Gradient n Since V is a function of x, y, and z, the total differential is: n But also, n Both expression are true for any dx, dy, and dz. Thus: n Note: Gradient of a scalar is a vector. President University Erwin Sitompul EEM 6/13

Chapter 4 Energy and Potential Gradient n Introducing the vector operator for gradient: We now can relate E and V as: Rectangular Cylindrical Spherical President University Erwin Sitompul EEM 6/14

Chapter 4 Energy and Potential Gradient n Example Given the potential field, V = 2 x 2 y– 5 z, and a point P(– 4, 3, 6), find V, E, direction of E, D, and ρv. President University Erwin Sitompul EEM 6/15

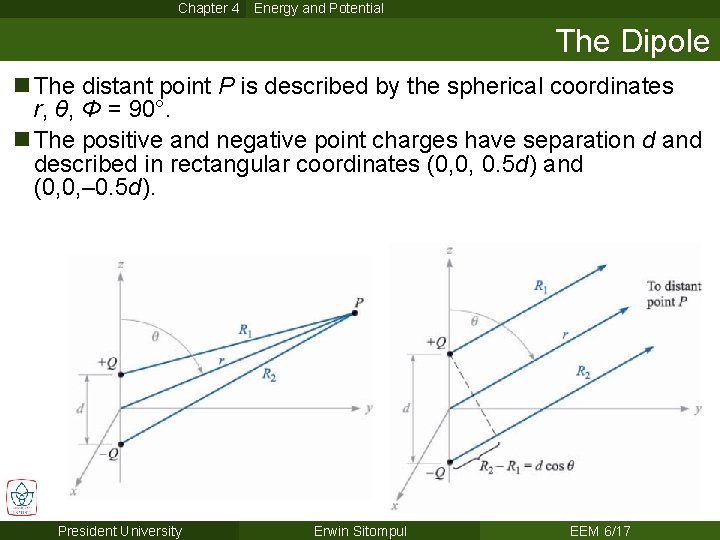
Chapter 4 Energy and Potential The Dipole n The dipole fields form the basis for the behavior of dielectric materials in electric field. n The dipole will be discussed now and will serve as an illustration about the importance of the potential concept presented previously. n An electric dipole, or simply a dipole, is the name given to two point charges of equal magnitude and opposite sign, separated by a distance which is small compared to the distance to the point P at which we want to know the electric and potential fields. President University Erwin Sitompul EEM 6/16

Chapter 4 Energy and Potential The Dipole n The distant point P is described by the spherical coordinates r, θ, Φ = 90°. n The positive and negative point charges have separation d and described in rectangular coordinates (0, 0, 0. 5 d) and (0, 0, – 0. 5 d). President University Erwin Sitompul EEM 6/17

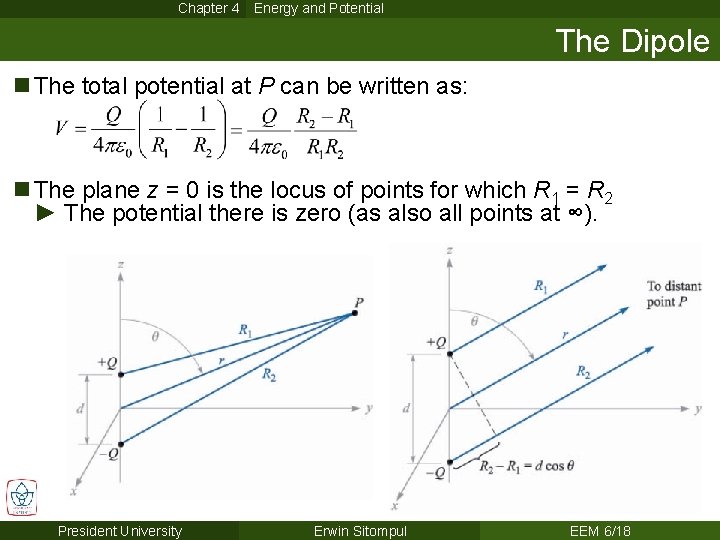
Chapter 4 Energy and Potential The Dipole n The total potential at P can be written as: n The plane z = 0 is the locus of points for which R 1 = R 2 ► The potential there is zero (as also all points at ∞). President University Erwin Sitompul EEM 6/18

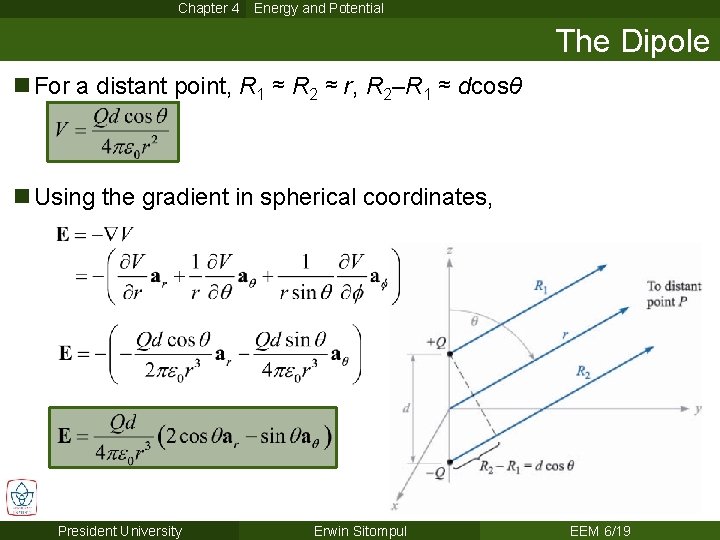
Chapter 4 Energy and Potential The Dipole n For a distant point, R 1 ≈ R 2 ≈ r, R 2–R 1 ≈ dcosθ n Using the gradient in spherical coordinates, President University Erwin Sitompul EEM 6/19

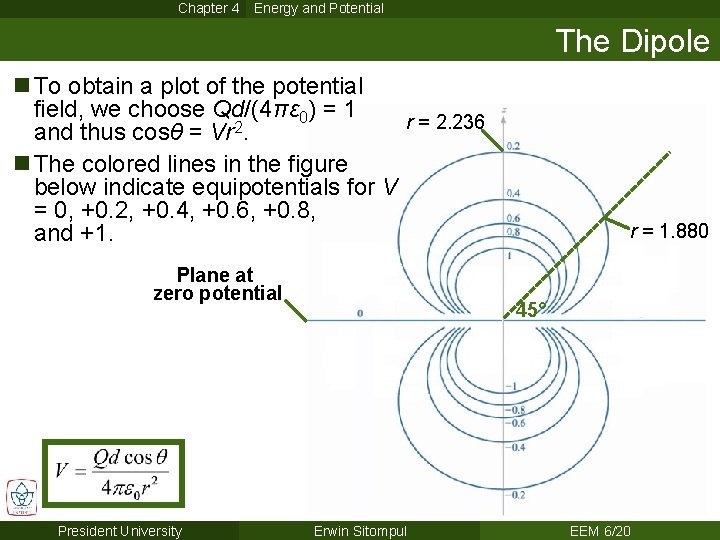
Chapter 4 Energy and Potential The Dipole n To obtain a plot of the potential field, we choose Qd/(4πε 0) = 1 r = 2. 236 and thus cosθ = Vr 2. n The colored lines in the figure below indicate equipotentials for V = 0, +0. 2, +0. 4, +0. 6, +0. 8, and +1. Plane at zero potential President University r = 1. 880 45° Erwin Sitompul EEM 6/20

Chapter 4 Energy and Potential The Dipole n The potential field of the dipole may be simplified by making use of the dipole moment. n If the vector length directed from –Q to +Q is identified as d, then the dipole moment is defined as Qd and is assigned the symbol p. n Since d ar = d cosθ , we then have: • Dipole charges: • Point charge: President University Erwin Sitompul EEM 6/21

Chapter 4 Energy and Potential Exercise Problems 1. A charge in amount of 13. 33 n. C is uniformly distributed in a circular disk form, with the radius of 2 m. Determine the potential at a point on the axis, 2 m from the disk. Compare this potential with that which results if all the charge is at the center of the disk. (Sch. S 62. E 3) Answer: 49. 7 V, 60 V. 2. For the point P(3, 60°, 2) in cylindrical coordinates and the potential field V = 10(ρ +1)z 2 cosφ V in free space, find at P: (a) V; (b) E; (c) D; (d) ρv; (e) d. V/d. N; (f) a. N. (Hay. E 5. S 112. 23) Answer: (a) 80 V; (b) – 20 aρ + 46. 2 aφ – 80 az V/m; (c) – 177. 1 aρ + 409 aφ – 708 az p. C/m 2; (d) – 334 p. C/m 3; (e) 94. 5 V/m; (f) 0. 212 aρ – 0. 489 aφ +0. 846 az 3. Two opposite charges are located on the z-axis and centered on the origin, configuring as an electric dipole is located at origin. The distance between the two charges, each with magnitude of 1 n. C, is given by 0. 1 nm. The electric potential at A(0, 1, 1) nm is known to be 2 V. Find out the electric potential at B(1, 1, 1) nm. Hint: Do not assume that A and B are distant points. Determine E due to both charges first, then calculate the potential difference. (EEM. Pur 5. N 4) Answer: 1. 855 V. President University Erwin Sitompul EEM 6/22