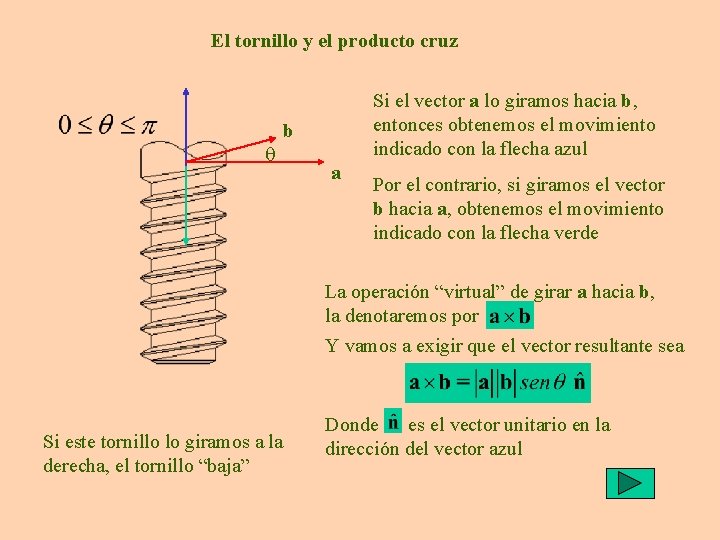
El tornillo y el producto cruz q Si

El tornillo y el producto cruz q Si el vector a lo giramos hacia b, entonces obtenemos el movimiento indicado con la flecha azul b a Por el contrario, si giramos el vector b hacia a, obtenemos el movimiento indicado con la flecha verde La operación “virtual” de girar a hacia b, la denotaremos por Y vamos a exigir que el vector resultante sea Si este tornillo lo giramos a la derecha, el tornillo “baja” Donde es el vector unitario en la dirección del vector azul

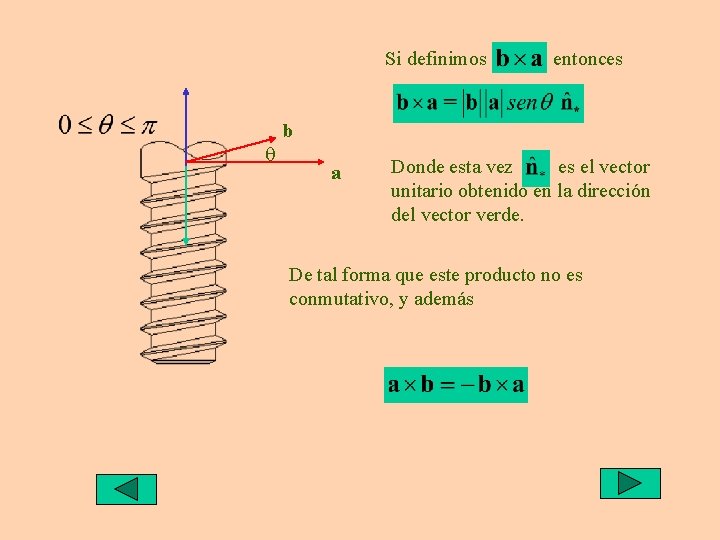
Si definimos q entonces b a Donde esta vez es el vector unitario obtenido en la dirección del vector verde. De tal forma que este producto no es conmutativo, y además

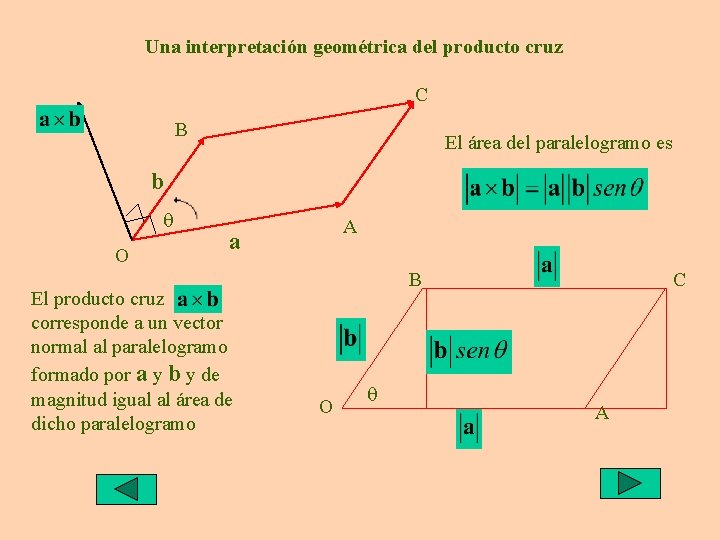
Una interpretación geométrica del producto cruz C B El área del paralelogramo es b q O A a El producto cruz corresponde a un vector normal al paralelogramo formado por a y b y de magnitud igual al área de dicho paralelogramo B O q C A

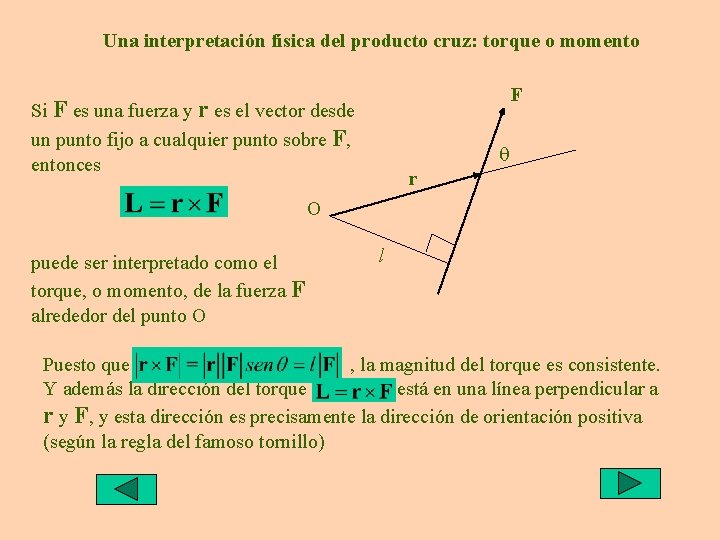
Una interpretación física del producto cruz: torque o momento F Si F es una fuerza y r es el vector desde un punto fijo a cualquier punto sobre F, entonces q r O puede ser interpretado como el torque, o momento, de la fuerza F alrededor del punto O l Puesto que , la magnitud del torque es consistente. Y además la dirección del torque está en una línea perpendicular a r y F, y esta dirección es precisamente la dirección de orientación positiva (según la regla del famoso tornillo)

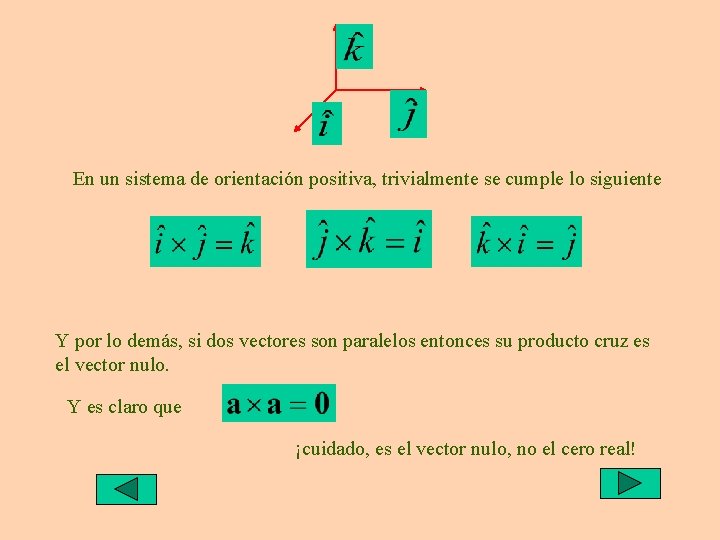
En un sistema de orientación positiva, trivialmente se cumple lo siguiente Y por lo demás, si dos vectores son paralelos entonces su producto cruz es el vector nulo. Y es claro que ¡cuidado, es el vector nulo, no el cero real!

Representación en componentes del vector Sean a y b dos vectores no paralelos, con representación en componentes Nuestro objetivo será encontrar los valores de p 1, p 2 y p 3 tales que El vector es perpendicular a ambos vectores, entonces ¡Este sistema, por sí solo, tiene muchísimas soluciones!

Las infinitas soluciones del sistema anterior están dadas por Estas soluciones las podemos escribir de forma simétrica como Siendo, ahora, la constante l a descubrir. Necesitamos imponer la condición de la magnitud del vector producto cruz. Es decir debemos obtener información de

Esta última ecuación traducida a sus componentes, nos queda Pero de la ecuación anterior podemos obtener

Desarrollando con paciencia estas expresiones podemos comprobar que son iguales. De modo que obtenemos la ecuación Se puede verificar que para l = 1 corresponde a un sistema orientación positiva, y para l = - 1 corresponde a un sistema orientado negativamente (recuerde el tornillo). Para l = 1 obtenemos

Con estas ecuaciones calculamos los valores de p 1, p 2 y p 3 Una regla nemotécnica (es decir algo solo para recordar pero que no tiene ningún valor matemático) es como sigue