Digital Lesson Operations on Rational Expressions Rational expressions












- Slides: 12

Digital Lesson Operations on Rational Expressions

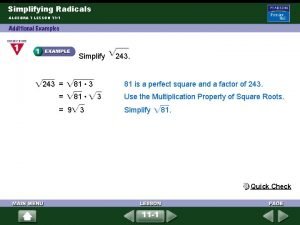
Rational expressions are fractions in which the numerator and denominator are polynomials and the denominator does not equal zero. Example: Simplify . , x– 3 0 , x 3 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 2

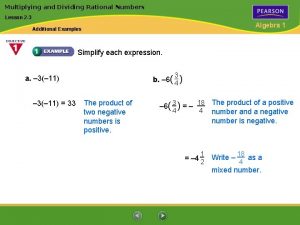
To multiply rational expressions: 1. Factor the numerator and denominator of each fraction. 2. Multiply the numerators and denominators of each fraction. 3. Divide by the common factors. 4. Write the answer in simplest form. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 3

Example: Multiply . Factor the numerator and denominator of each fraction. Multiply. Divide by the common factors. Write the answer in simplest form. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 4

To divide rational expressions: 1. Multiply the dividend by the reciprocal of the divisor. The reciprocal of is . 2. Multiply the numerators. Then multiply the denominators. 3. Divide by the common factors. 4. Write the answer in simplest form. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 5

Example: Divide . Multiply by the reciprocal of the divisor. Factor and multiply. Divide by the common factors. Simplest form Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 6

The least common multiple (LCM) of two or more numbers is the least number that contains the prime factorization of each number. Examples: 1. Find the LCM of 10 and 4. 10 = (5 • 2) factors of 10 4 = (2 • 2) LCM = 2 • 5 = 20 factors of 4 2. Find the LCM of 4 x 2 + 4 x and x 2 + 2 x + 1. 4 x 2 + 4 x = (4 x)(x +1) = 2 • 2 x (x + 1) x 2 + 2 x + 1 = (x +1) factors of x 2 + 2 x + 1 LCM = 2 • 2 x (x +1) = 4 x 3 + 8 x 2 + 4 x factors of 4 x 2 + 4 x Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 7

Fractions can be expressed in terms of the least common multiple of their denominators. Example: Write the fractions and in terms of the LCM of the denominators. The LCM of the denominators is 12 x 2(x – 2). LCM Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 8

To add rational expressions: 1. If necessary, rewrite the fractions with a common denominator. 2. Add the numerators of each fraction. To subtract rational expressions: 1. If necessary, rewrite the fractions with a common denominator. 2. Subtract the numerators of each fraction. Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 9

Example: Add Example: Subtract Copyright © by Houghton Mifflin Company, Inc. All rights reserved. . . 10

Two rational expressions with different denominators can be added or subtracted after they are rewritten with a common denominator. Example: Add Copyright © by Houghton Mifflin Company, Inc. All rights reserved. . 11

Example: Subtract . Add numerators. Factor. Divide. Simplest form Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 12
 Lesson 11-3 solving radical equations answers
Lesson 11-3 solving radical equations answers Lesson 2: multiplying and dividing rational expressions
Lesson 2: multiplying and dividing rational expressions Order of operations and evaluating expressions
Order of operations and evaluating expressions Rational expressions and functions
Rational expressions and functions How do you simplify a rational expression
How do you simplify a rational expression Complex rational expressions
Complex rational expressions 11-4 practice multiplying and dividing rational expressions
11-4 practice multiplying and dividing rational expressions 6-2 multiplying and dividing radical expressions
6-2 multiplying and dividing radical expressions Reducing rational expressions to lowest terms
Reducing rational expressions to lowest terms Multiplying and dividing rational expressions quizlet
Multiplying and dividing rational expressions quizlet Rational expressions jeopardy
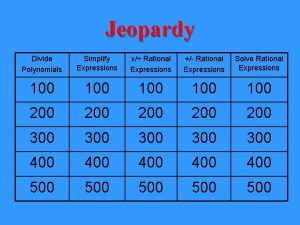
Rational expressions jeopardy Chapter 9 rational expressions and equations answers
Chapter 9 rational expressions and equations answers Practice 9-5 adding and subtracting rational expressions
Practice 9-5 adding and subtracting rational expressions