Degenerate Fermi gas 0 TTF T0 When TTF

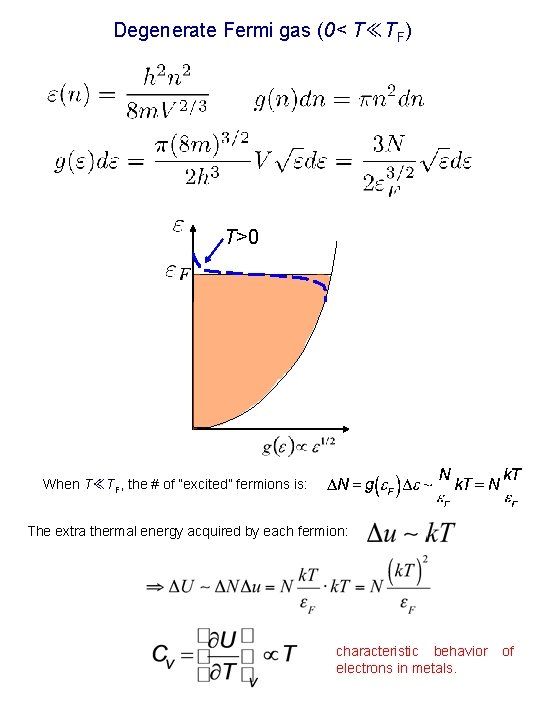
Degenerate Fermi gas (0< T≪TF) T>0 When T≪TF, the # of “excited” fermions is: The extra thermal energy acquired by each fermion: characteristic behavior electrons in metals. of

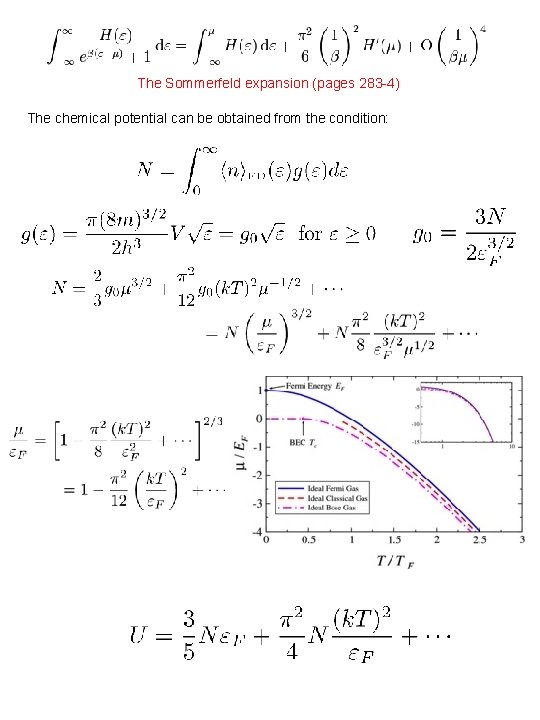
The Sommerfeld expansion (pages 283 -4) The chemical potential can be obtained from the condition:

Two types of bosons: (a) Composite particles which contain an even number of fermions. The number of these particles is conserved if the energy does not exceed the dissociation/separation energy. (b) Particles associated with a field, of which the most important example is the photon. The number of these particles is not conserved: if the total energy of the field changes, particles would appear and disappear. The chemical potential of such particles is zero in equilibrium, regardless of density. Bosons are special: any # of bosons can occupy one quantum state (energy level) A layman’s definition: Bose-Einstein Condensation (BEC) is a special macrostate with macroscopic # of bosons occupying one quantum state (often, the ground state) of a bosonic system. As the system temperature is cooled below certain temperature TC, BEC spontaneously forms. It is a phase transition purely driven by quantum (exchange) effect. 4 3 2 1 Consider a special case of T = 0 K. What is the macrostate of a bosonic system? All the bosons (a macroscopic #) occupy the lowest energy level, i. e. the ground state, so that the system has lowest energy.

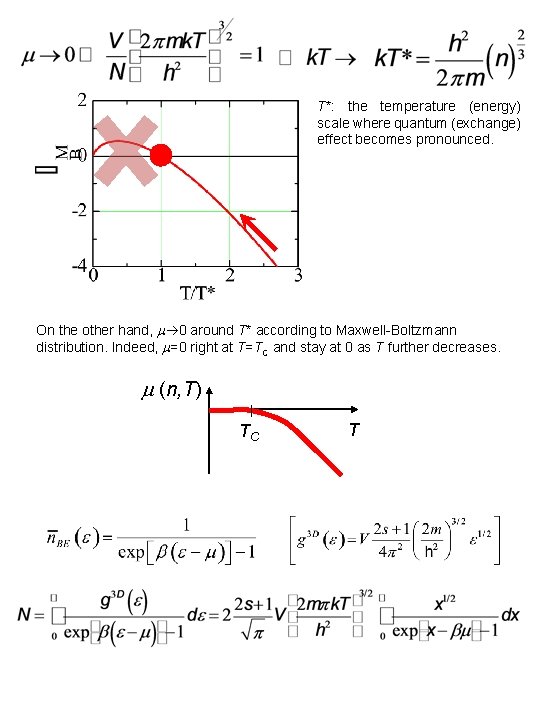
T*: the temperature (energy) scale where quantum (exchange) effect becomes pronounced. On the other hand, 0 around T* according to Maxwell-Boltzmann distribution. Indeed, =0 right at T=TC and stay at 0 as T further decreases. (n, T) TC T

Let us perform the integration at TC, i. e. , at =0. Critical temperature of BEC T>TC, the system can adjust (<0) to satisfy the constraint: What happens at T<TC? is already 0 at TC. The right hand side decreases as T 3/2… Resolving the paradox: The problem is caused by the behavior of the 3 D density of states and our use of the continuum approximation. Because g( )=0 at =0, our calculations of n ignored all the particles in the ground ( =0) state. At low energies, we have to take into account the discrete nature of quantum states. Excited states only! n( ) g( )

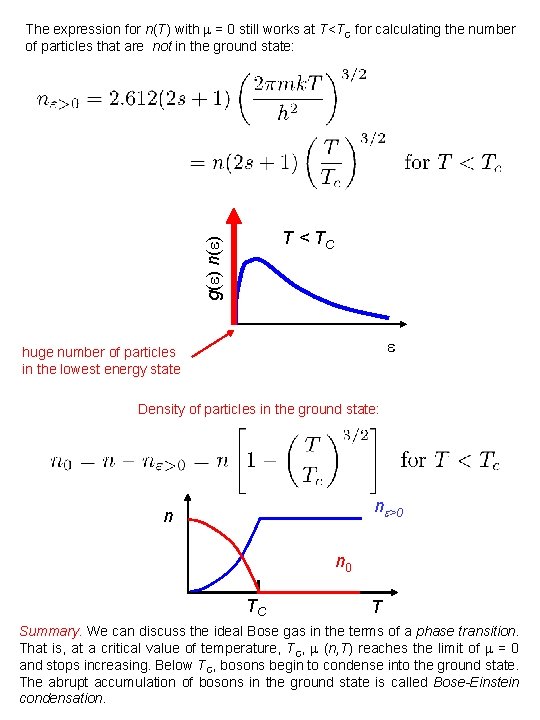
The expression for n(T) with = 0 still works at T<TC for calculating the number of particles that are not in the ground state: g( ) n( ) T < TC huge number of particles in the lowest energy state Density of particles in the ground state: n >0 n n 0 TC T Summary. We can discuss the ideal Bose gas in the terms of a phase transition. That is, at a critical value of temperature, TC, (n, T) reaches the limit of = 0 and stops increasing. Below TC, bosons begin to condense into the ground state. The abrupt accumulation of bosons in the ground state is called Bose-Einstein condensation.