Danny Z Chen 1 Rajasekhar Inkulu 2 Haitao

Danny Z. Chen 1 Rajasekhar Inkulu 2 Haitao Wang 3 1 University of Notre Dame 2 Indian Institute of Technology 3 Utah State University So. CG 2014

A polygonal domain § A set of h disjoint polygonal obstacles with a total of n vertices § Free space: the space outside the obstacles h<<n is possible

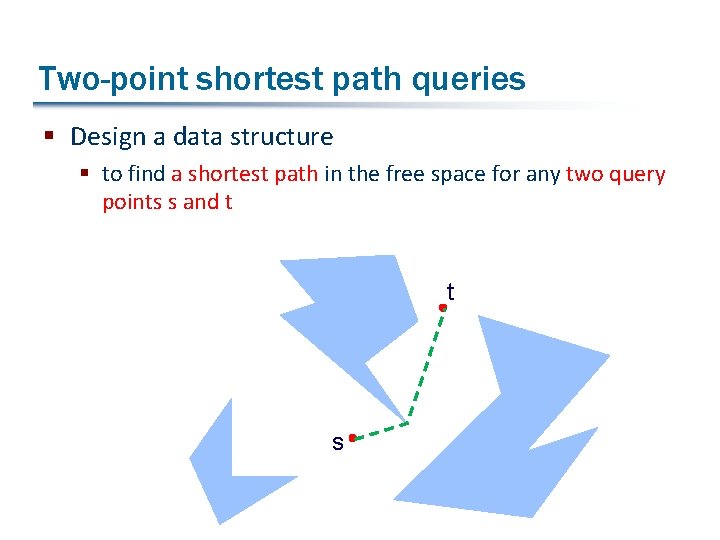
Two-point shortest path queries § Design a data structure § to find a shortest path in the free space for any two query points s and t t s

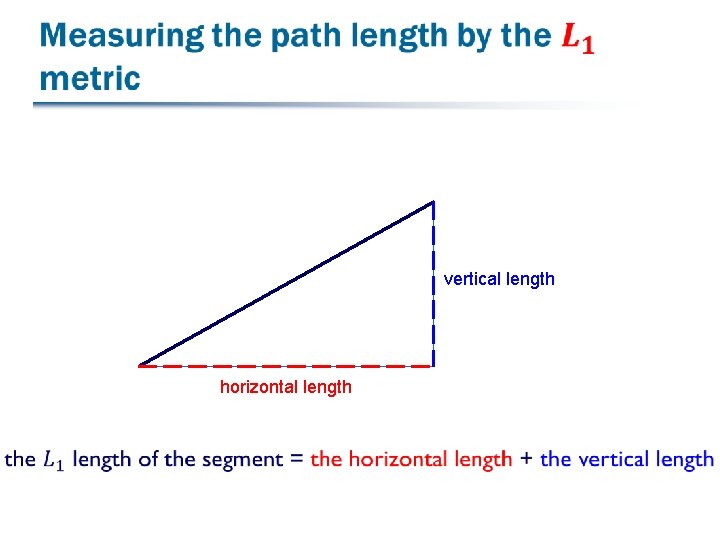
vertical length horizontal length

Previous work and our results § both bounded by O(n+h 2+ε)

Other related work §

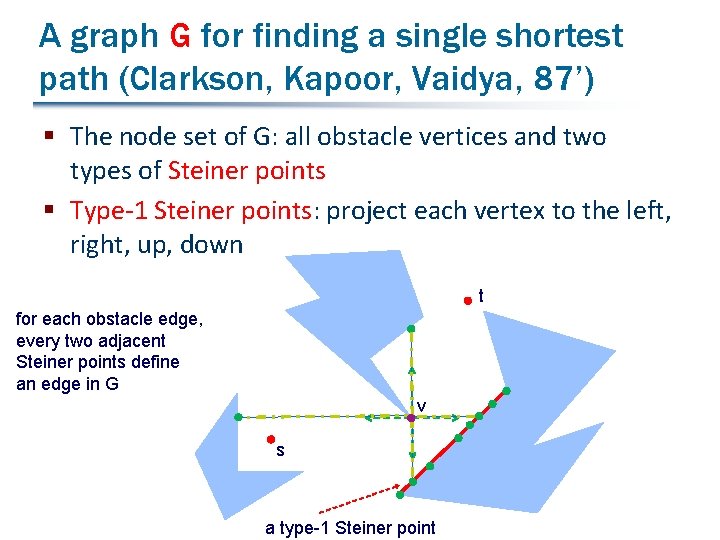
A graph G for finding a single shortest path (Clarkson, Kapoor, Vaidya, 87’) § The node set of G: all obstacle vertices and two types of Steiner points § Type-1 Steiner points: project each vertex to the left, right, up, down t for each obstacle edge, every two adjacent Steiner points define an edge in G v s a type-1 Steiner point

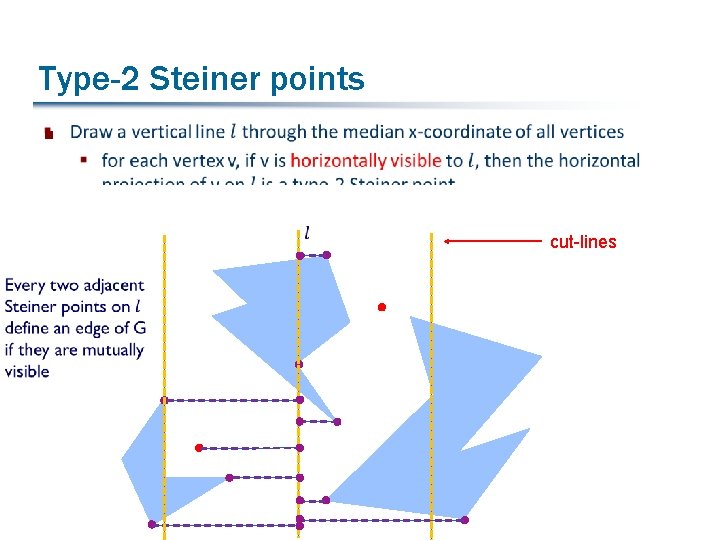
Type-2 Steiner points § cut-lines

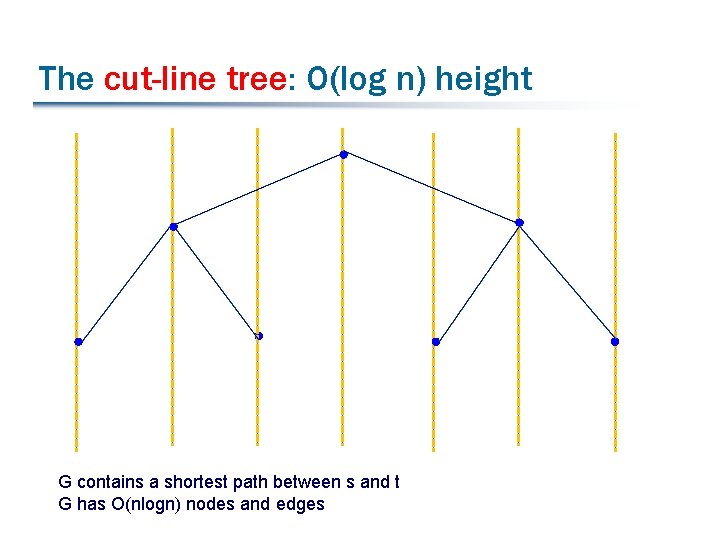
The cut-line tree: O(log n) height G contains a shortest path between s and t G has O(nlogn) nodes and edges

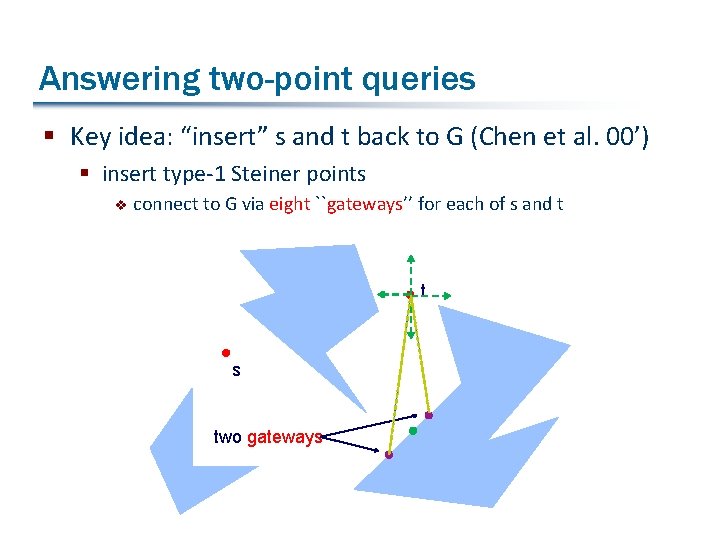
Answering two-point queries § Key idea: “insert” s and t back to G (Chen et al. 00’) § insert type-1 Steiner points v connect to G via eight ``gateways’’ for each of s and t t s two gateways

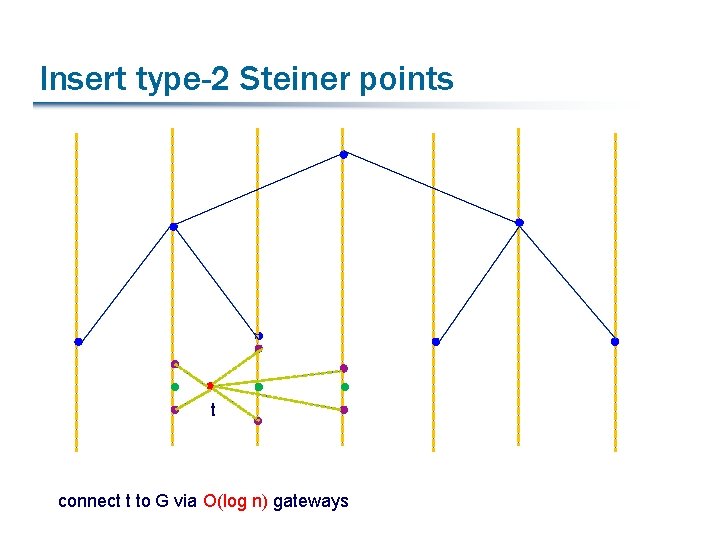
Insert type-2 Steiner points t connect t to G via O(log n) gateways

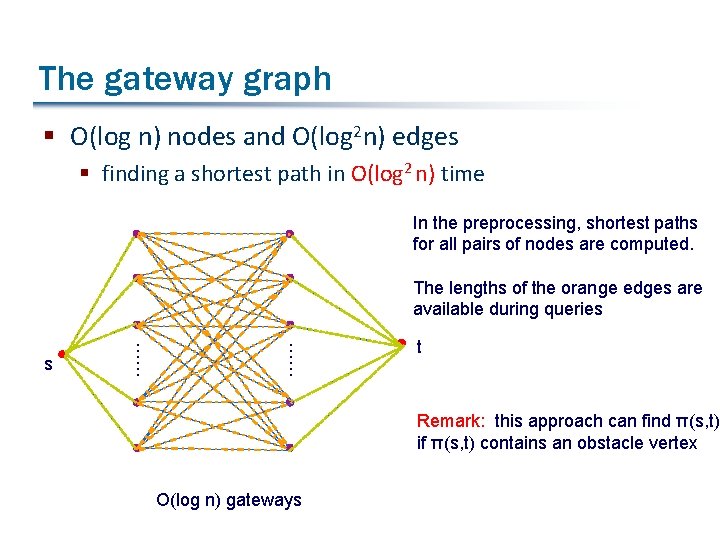
The gateway graph § O(log n) nodes and O(log 2 n) edges § finding a shortest path in O(log 2 n) time In the preprocessing, shortest paths for all pairs of nodes are computed. The lengths of the orange edges are available during queries …… …… s t Remark: this approach can find π(s, t) if π(s, t) contains an obstacle vertex O(log n) gateways

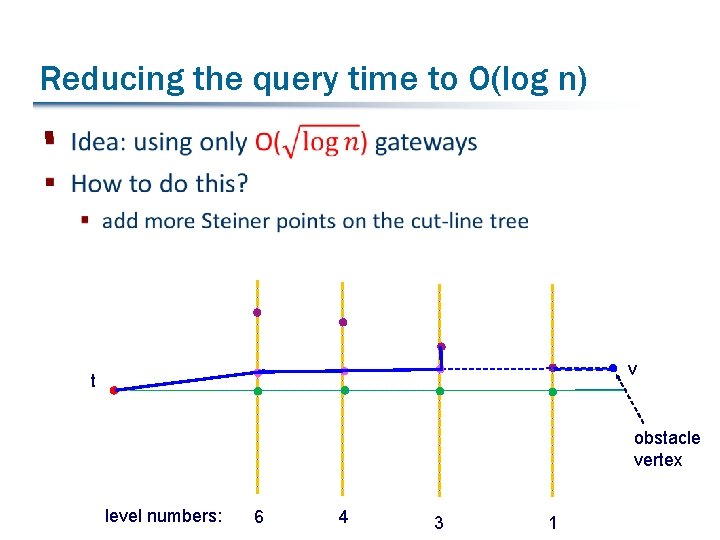
Reducing the query time to O(log n) § v t obstacle vertex level numbers: 6 4 3 1

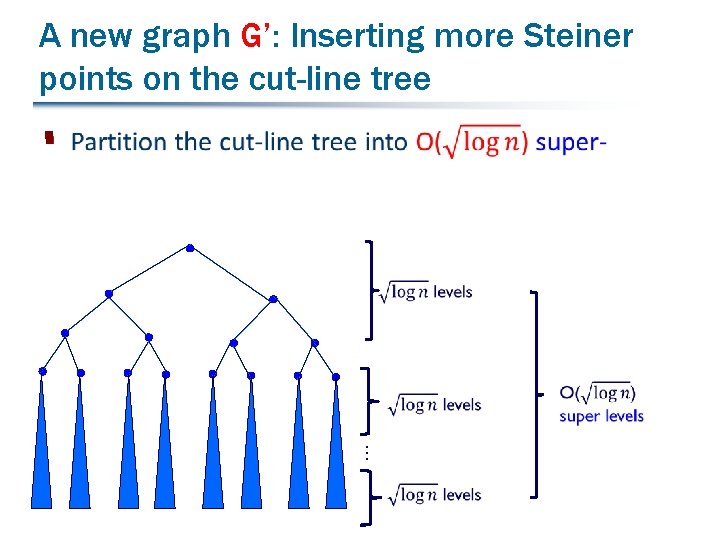
A new graph G’: Inserting more Steiner points on the cut-line tree § …

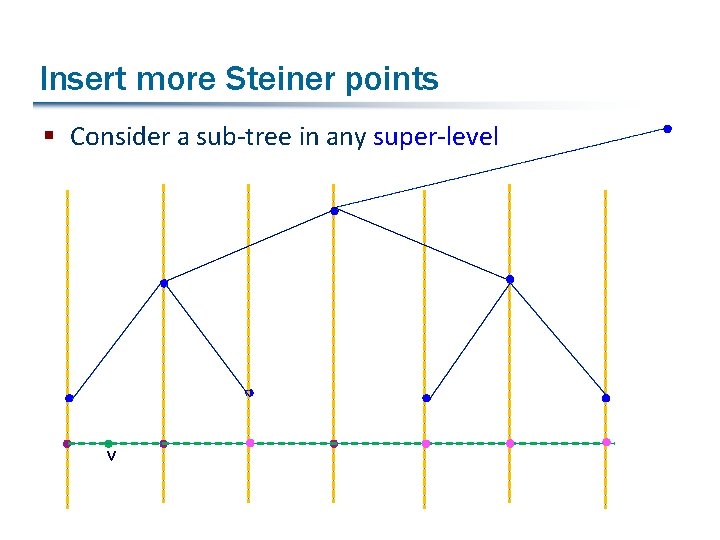
Insert more Steiner points § Consider a sub-tree in any super-level v

The new graph G’ §

The convex case: all obstacles are convex §

Non-convex case § A special case: assume their convex hulls are pairwise disjoint § The general case can be reduced to this special case using the extended corridor structure § The ocean M: the free space outside the convex hulls § Bays: free space not in M bays

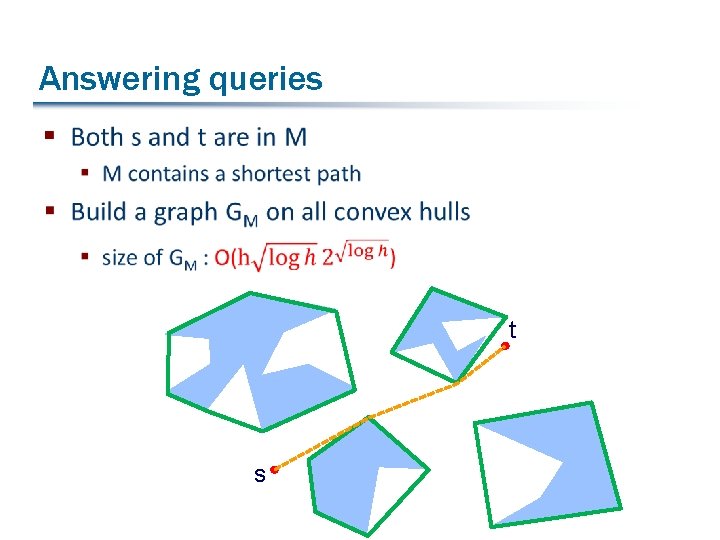
Answering queries § t s

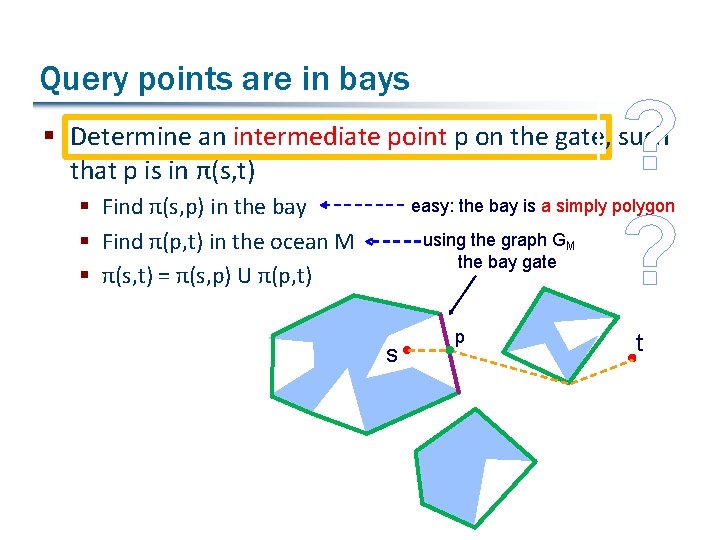
Query points are in bays ? ? § Determine an intermediate point p on the gate, such that p is in π(s, t) § Find π(s, p) in the bay § Find π(p, t) in the ocean M § π(s, t) = π(s, p) U π(p, t) easy: the bay is a simply polygon using the graph GM the bay gate s p t

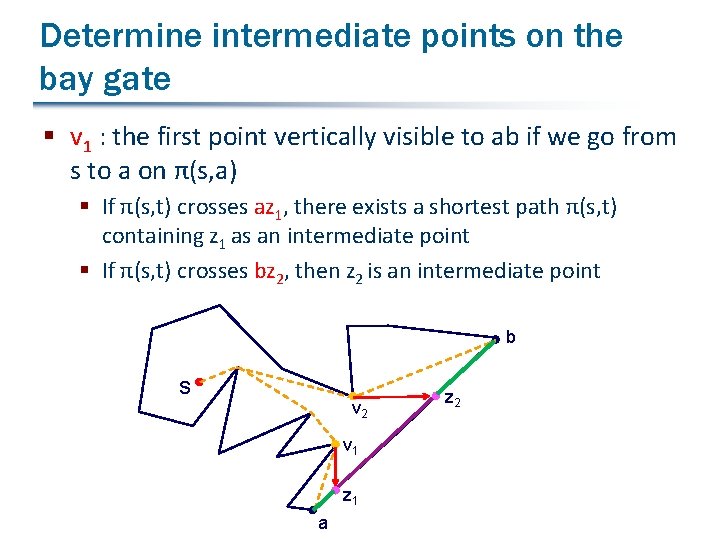
Determine intermediate points on the bay gate § v 1 : the first point vertically visible to ab if we go from s to a on π(s, a) § If π(s, t) crosses az 1, there exists a shortest path π(s, t) containing z 1 as an intermediate point § If π(s, t) crosses bz 2, then z 2 is an intermediate point b s v 2 v 1 z 1 a z 2

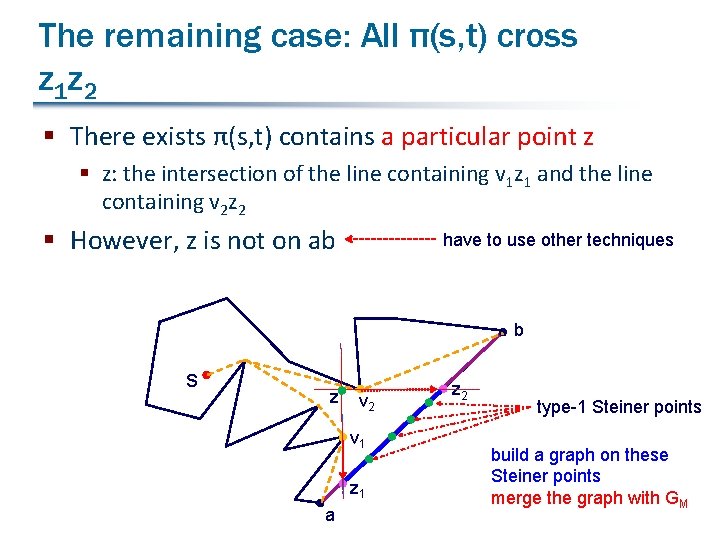
The remaining case: All π(s, t) cross z 1 z 2 § There exists π(s, t) contains a particular point z § z: the intersection of the line containing v 1 z 1 and the line containing v 2 z 2 § However, z is not on ab have to use other techniques b s z v 2 v 1 z 1 a z 2 type-1 Steiner points build a graph on these Steiner points merge the graph with GM

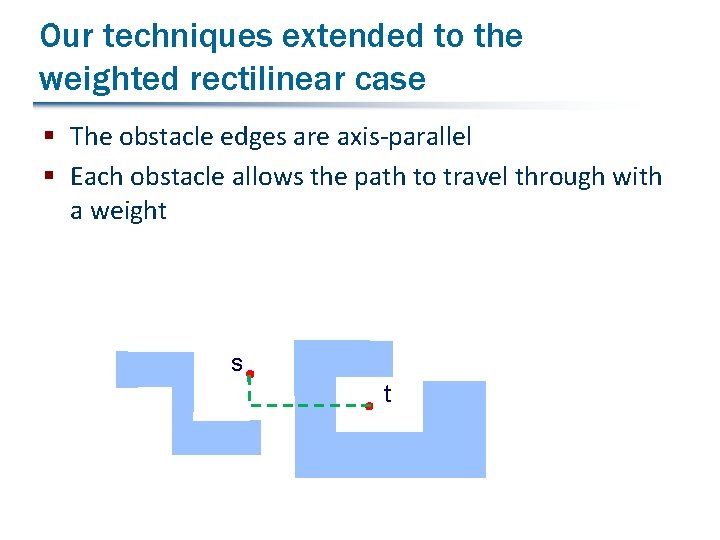
Our techniques extended to the weighted rectilinear case § The obstacle edges are axis-parallel § Each obstacle allows the path to travel through with a weight s t

Results for the weighted rectilinear case § both bounded by O(n 2+ε)

Thank You