COSC 3340 Introduction to Theory of Computation University

COSC 3340: Introduction to Theory of Computation University of Houston Dr. Verma Lecture 27 1 Lecture 27 Uof. H - COSC 3340 - Dr. Verma

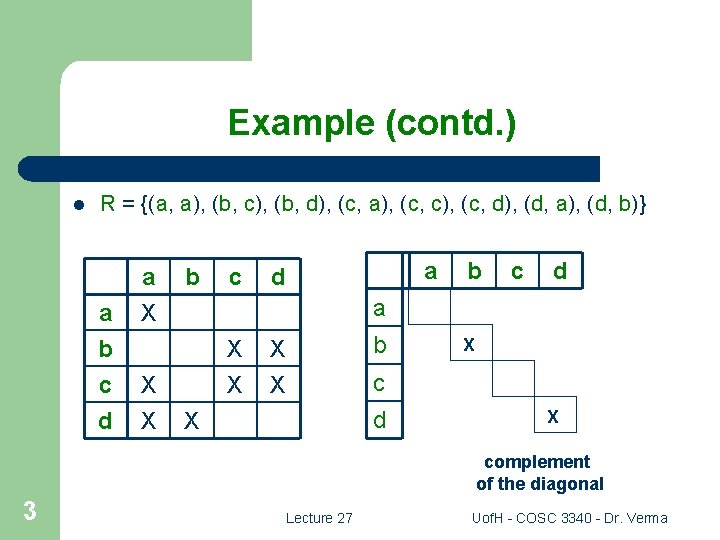
Diagonalization Principle l l l Let S be any nonempty set and R any relation on S. The principle states that: the complement of the diagonal is different from each row. Can be generalized to relations on two sets, etc. Example: Let S = {a, b, c, d}. R = {(a, a), (b, c), (b, d), (c, a), (c, c), (c, d), (d, a), (d, b)} 2 Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Example (contd. ) l R = {(a, a), (b, c), (b, d), (c, a), (c, c), (c, d), (d, a), (d, b)} a b c d a X b a d b c d a X X c b X X X c d X X complement of the diagonal 3 Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Applications of Diagonalization. l l The principle is very useful to show that enumerations of some sets cannot be exhaustive. For example, one can show: 1. 2. 3. 4 2 N is uncountable. The set of real numbers in the interval [0, 1] is uncountable. (Exercise) The set {<M, w> | M accepts w} is not Turing decidable. Lecture 27 Uof. H - COSC 3340 - Dr. Verma

2 N is Uncountable. l l l 5 Suppose that it is countably infinite. Then there is an enumeration 2 N = {S 0, S 1, S 2, . . . } using the bijection between N and 2 N. Let D = { i N | i Si}. D is a subset of N so it belongs to 2 N. So, D = Sk for some k N. Lecture 27 Uof. H - COSC 3340 - Dr. Verma

2 N is Uncountable (contd. ) l We ask whether k Sk. – – l 6 Case 1. k Sk. By definition of D, k D, but D = Sk, so contradiction. Case 2. k Sk. By definition of D, k D, but D = Sk, again contradiction. Hence our hypothesis that 2 N is countable is false (q. e. d. ). Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Where was Diagonalization used? l Consider N X {S 0, S 1, . . }. 0 s 1 1 2 X 3 . . X X X s 2 s 3 X . X X . l 7 D is the complement of the diagonal of this infinite relation. Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Proof for ATM = {<M, w> | M accepts w} l l Suppose that H is a decider for ATM. On input <M, w>, H halts and accepts if M accepts w and H halts and rejects if M rejects w. H(<M, w>) = accept if M accepts w reject if M does not accept w. l 8 Now we construct a new Turing machine D with H as a subroutine. D calls H to determine what M does when input to M is its own description <M>. Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Proof for ATM (contd. ) D = “On input <M>, where M is a TM: 1. 2. Run H on input <M, <M>>. Output the opposite of what H outputs; that is, if H accepts, reject and if H rejects, accept. ” D(<M>) = accept if M does not accept <M> reject if M accepts <M>. What happens when we run D with its own description <D> as input? In that case we get D(<D>) = accept if D does not accept <D> reject if D accepts <D>. 9 Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Proof for ATM (contd. ) l Basically, – – – l The machine take the following actions, with the last line being the contradiction. – – – 10 Assume that a TM H decides ATM. Then use H to build a TM D that when given input < M > accepts exactly when M does not accept input < M >. Finally, run D on itself. H accepts <M, w> exactly when M accepts w. D rejects < M > exactly when M accepts < M >. D rejects < D > exactly when D accepts < D >. Lecture 27 Uof. H - COSC 3340 - Dr. Verma

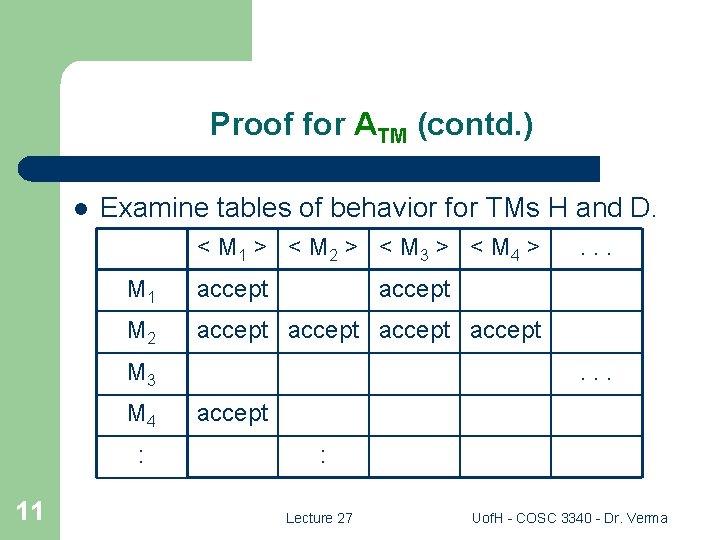
Proof for ATM (contd. ) l Examine tables of behavior for TMs H and D. < M 1 > < M 2 > < M 3 > < M 4 > M 1 accept M 2 accept accept M 3 M 4 : 11 . . . accept : Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Another Perspective on Halting Problem l l 12 If L is a Turing-decidable language then L’ (complement of L) is also Turing-decidable. If it were possible to predict for any TM M and any input string whether or not M would halt on that input, then every Turing-acceptable language would also be Turing decidable. Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Another Perspective l K 0 = { (M) (w) | Turing machine M accepts input string w. } If K 0 is decidable then every Turing acceptable language is also Turing decidable. K 0 is Turing acceptable. – 13 Every Turing acceptable language is Turing decidable iff K 0 is Turing decidable. Lecture 27 Uof. H - COSC 3340 - Dr. Verma

Another Perspective l l l 14 If K 0 is decidable, K 1 = { (M) | TM M accepts input string (M) } would also be Turing decidable. If K 1 is decidable then so is complement of K 1, K 1’, is not even Turing acceptable K 1’ = {w {I, c}* | w is not the encoding of any TM M, or w = (M) for some M that does not accept its own encoding} Lecture 27 Uof. H - COSC 3340 - Dr. Verma