Complements of Languages in NP Osama Awwad Department

Complements of Languages in NP Osama Awwad Department of Computer Science Western Michigan University 19 June 2021

Complement classes In general, if C is a complexity class n co-C is the complement class, containing all complements of languages in C n C implies ( * - L) co-C ¨ ( * - L) C implies L co-C ¨L n Some classes closed under complement: ¨ e. g. co-P = P

Co-P = P n Given a polynomial-time TM M for L, we can modify M to accept the complement of L as follows: n Make each accepting state of M a nonaccepting state from which there are no moves. Thus, if M accepts, the new TM (L) will halt without accepting. n Create a new state q, which is the only accepting state in the new TM. For each state-symbol combination that has no move, the new TM enters state q, whereupon it accepts and halts.

Co-NP NP (nondeterministic polynomial-time): class of problems for which, if the answer is yes, then there's a polynomial-size proof of that fact that you can check in polynomial time. n Co-NP: Co-NP The set of languages whose complements are in NP n

Example Input: graph G=(V, E) n Does G have a Hamiltonian cycle? n § Hamiltonian cycle: cycle visiting each vertex exactly once If G has a Hamiltonian cycle then let us take a promised Hamiltonian cycle – we can check if this is indeed one in O(n) time! n Hamiltonian cycle is in NP n • Does G have no Hamiltonian cycle?

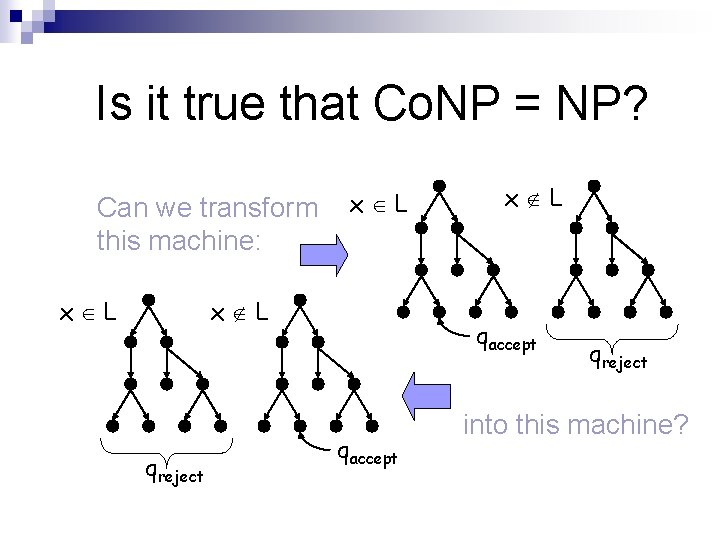
Is it true that Co. NP = NP? Can we transform this machine: x L x L qreject x L qaccept qreject into this machine?

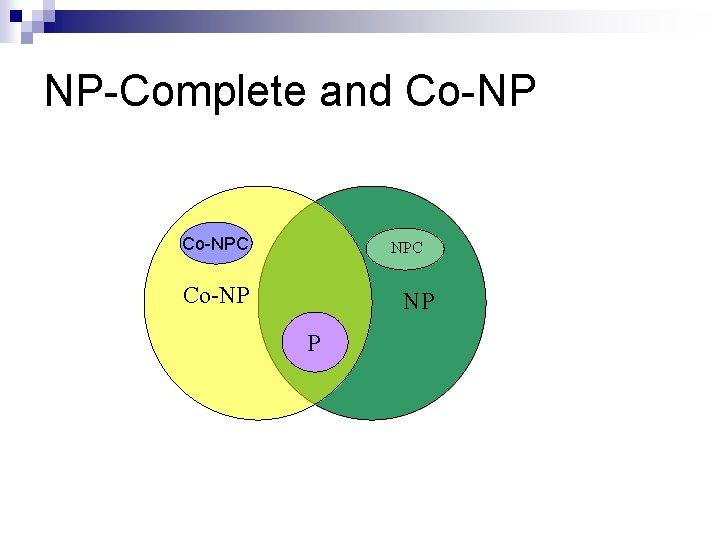
NP-Complete and Co-NP n n n Every language in P has its complement also in P, and therefore in NP. We believe that none of the NP-complete problems have their complements in NP. no NP-complete problem is in Co-NP. We believe the complements of NP-complete problems, which are by definition in Co-NP, are not in NP.

NP-Complete and Co-NPC NPC Co-NP NP P

NP-Complete and Co-NP n Theorem NP=co-NP if and only if the complement of some NP-complete problem is in NP.

Proof n (Only if): Should NP and Co-NP be the same Every NP-complete problem L, being in NP, is also in co-NP ¨ The complement of a problem in Co-NP is in NP the complement of L is in NP ¨ n (If) Let P be an NP-complete problem ¨ Suppose Pc is in NP ¨ For each L in NP, there is a polynomial-time reduction of L to P ¨ Lc is polynomial reducible to Pc _ Lc is in NP ¨