Analyzing Graphs of Polynomials Section 3 2 First

Analyzing Graphs of Polynomials Section 3. 2

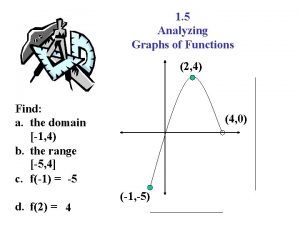
First a little review… Given the polynomial function of the form: If k is a zero, x = k Zero: _____ x = k Solution: _____ (x – k) Factor: _____ x - intercept If k is a real number, then k is also a(n) _________.

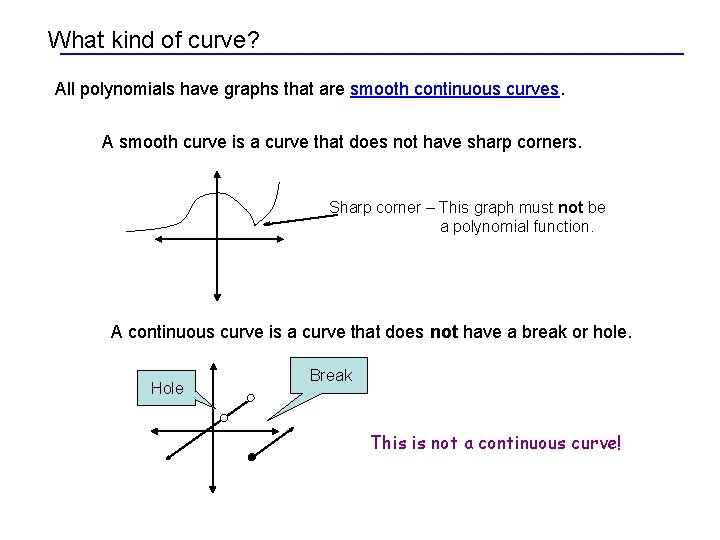
What kind of curve? All polynomials have graphs that are smooth continuous curves. A smooth curve is a curve that does not have sharp corners. Sharp corner – This graph must not be a polynomial function. A continuous curve is a curve that does not have a break or hole. Hole Break This is not a continuous curve!

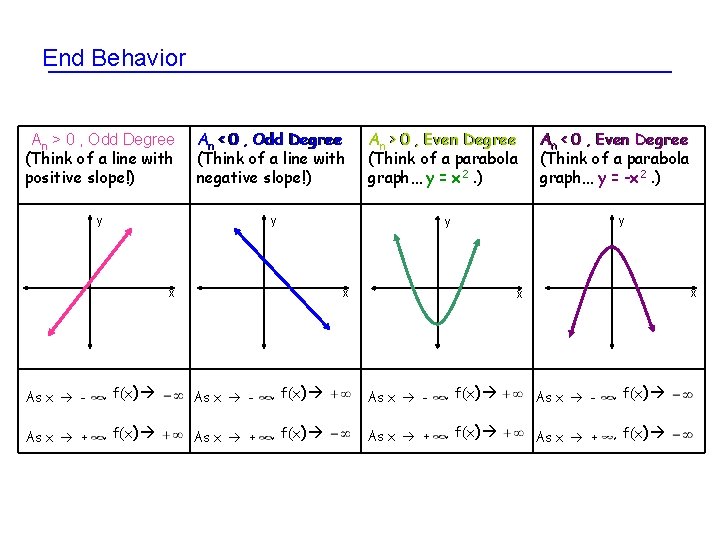
End Behavior An > 0 , Odd Degree (Think of a line with positive slope!) An < 0 , Odd Degree (Think of a line with negative slope!) y y x An > 0 , Even Degree (Think of a parabola graph… y = x 2. ) An < 0 , Even Degree (Think of a parabola graph… y = -x 2. ) y y x x x As x - , f(x) As x + , f(x)

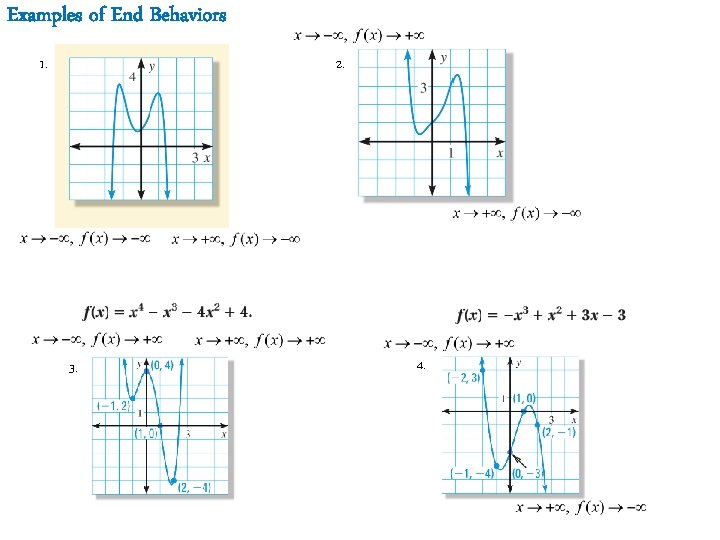
Examples of End Behaviors 1. 2. 3. 4.

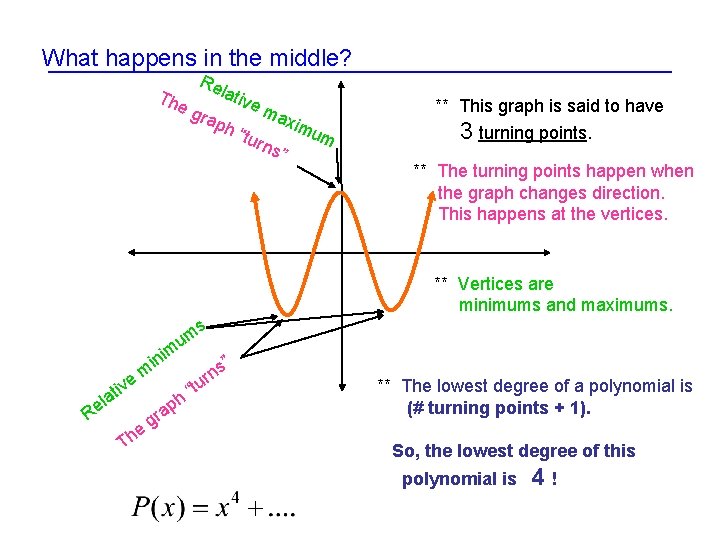
What happens in the middle? The Re gra lati ph ve ma xi “tur n s” mu ** This graph is said to have m 3 turning points. ** The turning points happen when the graph changes direction. This happens at the vertices. ** Vertices are minimums and maximums. s um e m ini m tiv a l e R e Th gr h ap “t ” ns r u ** The lowest degree of a polynomial is (# turning points + 1). So, the lowest degree of this polynomial is 4!

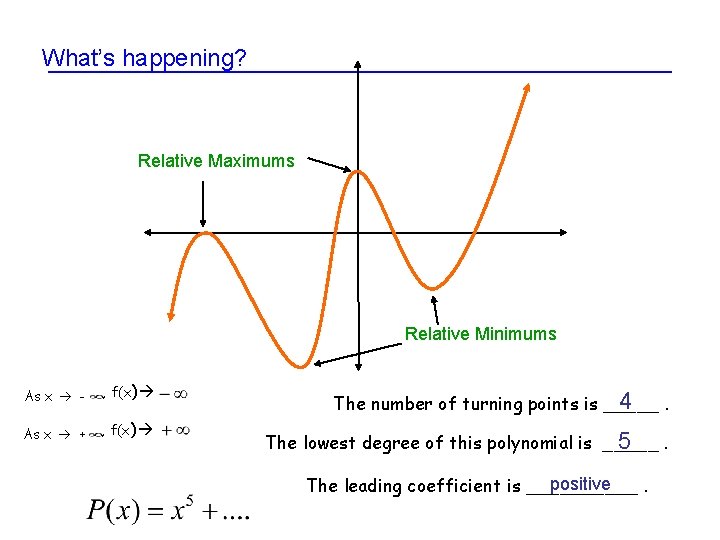
What’s happening? Relative Maximums Relative Minimums As x - , f(x) As x + , f(x) 4. The number of turning points is _____ The lowest degree of this polynomial is _____ 5. positive The leading coefficient is _____.

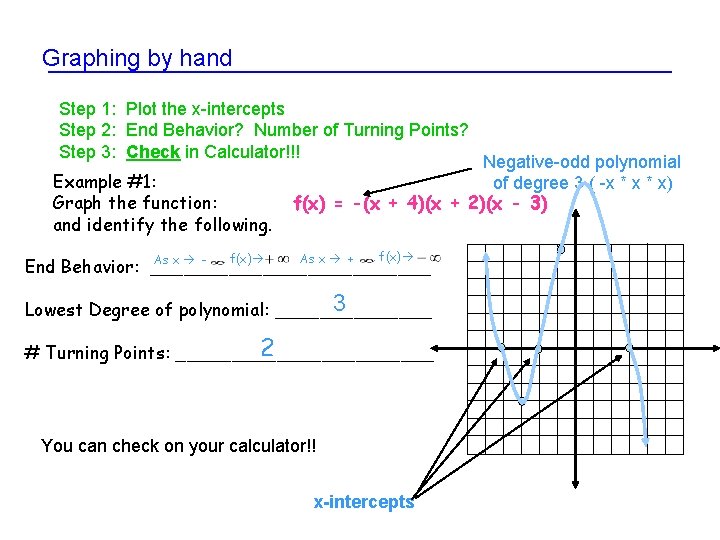
Graphing by hand Step 1: Plot the x-intercepts Step 2: End Behavior? Number of Turning Points? Step 3: Check in Calculator!!! Example #1: Graph the function: and identify the following. , f(x) Negative-odd polynomial of degree 3 ( -x * x) f(x) = -(x + 4)(x + 2)(x - 3) As x + , f(x) As x End Behavior: _____________ 3 Lowest Degree of polynomial: _______ 2 # Turning Points: ____________ You can check on your calculator!! x-intercepts

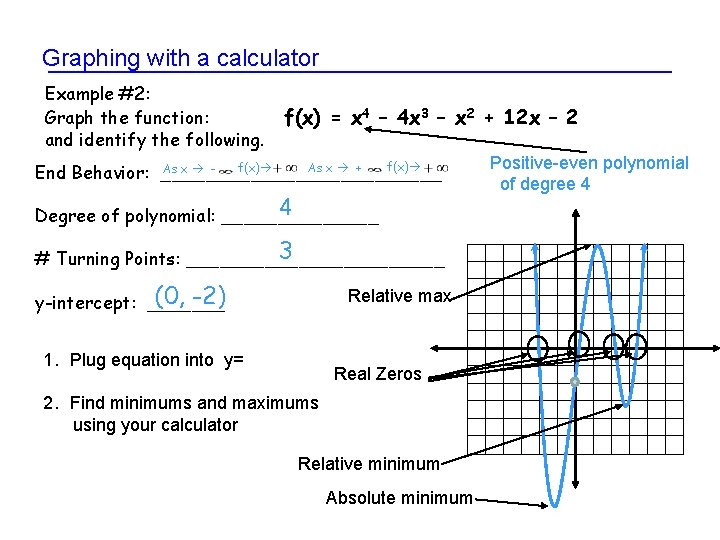
Graphing with a calculator Example #2: Graph the function: and identify the following. f(x) = x 4 – 4 x 3 – x 2 + 12 x – 2 , f(x) As x + As x - , f(x) End Behavior: _____________ 4 Degree of polynomial: _______ 3 # Turning Points: ____________ (0, -2) y-intercept: _______ Relative max 1. Plug equation into y= Real Zeros 2. Find minimums and maximums using your calculator Relative minimum Absolute minimum Positive-even polynomial of degree 4

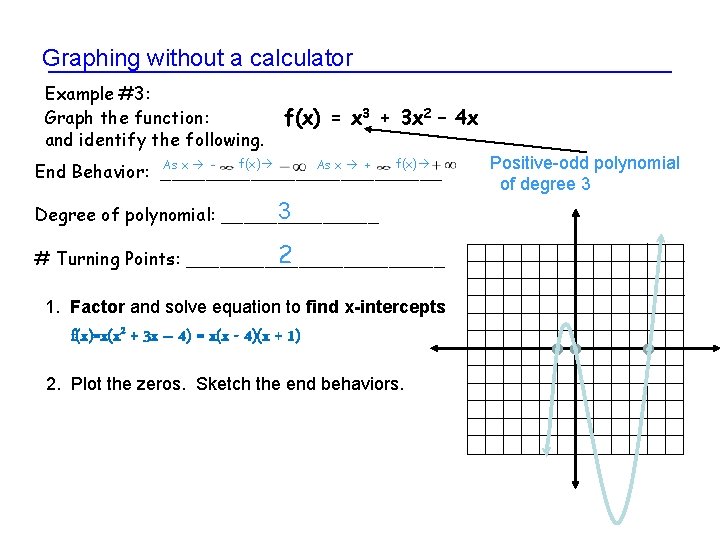
Graphing without a calculator Example #3: Graph the function: and identify the following. As x - f(x) = x 3 + 3 x 2 – 4 x , f(x) As x + End Behavior: _____________ 3 Degree of polynomial: _______ 2 # Turning Points: ____________ 1. Factor and solve equation to find x-intercepts f(x)=x(x 2 + 3 x – 4) = x(x - 4)(x + 1) 2. Plot the zeros. Sketch the end behaviors. Positive-odd polynomial of degree 3

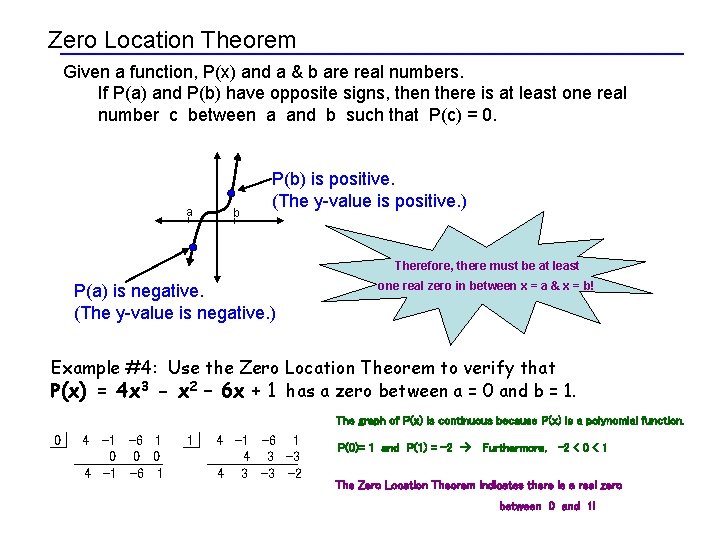
Zero Location Theorem Given a function, P(x) and a & b are real numbers. If P(a) and P(b) have opposite signs, then there is at least one real number c between a and b such that P(c) = 0. a b P(b) is positive. (The y-value is positive. ) Therefore, there must be at least P(a) is negative. (The y-value is negative. ) one real zero in between x = a & x = b! Example #4: Use the Zero Location Theorem to verify that P(x) = 4 x 3 - x 2 – 6 x + 1 has a zero between a = 0 and b = 1. The graph of P(x) is continuous because P(x) is a polynomial function. 0 4 -1 -6 1 0 0 0 4 -1 -6 1 1 4 -1 -6 1 4 3 -3 -2 P(0)= 1 and P(1) = -2 Furthermore, -2 < 0 < 1 The Zero Location Theorem indicates there is a real zero between 0 and 1!

Polynomial Functions: Real Zeros, Graphs, and Factors (x – c) • If P is a polynomial function and c is a real root, then each of the following is equivalent. is a factor of P • (x – c) _________________. • x=c is a real solution of P(x) = 0 _________________. • x=c is a real zero of P _________________. an x-intercept of the graph of y = P(x). • (c, 0) is _________________

Even & Odd Powers of (x – c) The exponent of the factor tells if that zero crosses over the x-axis or is a vertex. If the exponent of the factor is ODD, then the graph CROSSES the x-axis. If the exponent of the factor is EVEN, then the zero is a VERTEX. Try it. Graph y = (x + 3)(x – 4)2 Try it. Graph y = (x + 6)4 (x + 3)3

Assignment: Write the questions and show all work for each. pp. 301 -302 #1 -13 ODD, 17 & 19 (TI-83), 21 -29 ODD, 33, 35, 41, & 43