Algoritmos de rvore Geradora Mnima Algoritmo de Kruskal

Algoritmos de Árvore Geradora Mínima

Algoritmo de Kruskal entrada: G = (V, E), Lista de Adjacência de G: A(v), v V, matriz de pesos 1. ordenar as arestas e de G pelo valor de seus pesos 2. T ← ; 3. para-todo i = 1, . . . , |E| faça 4. se T U {e} é acíclico então 5. T ← T U {e}; 6. fim-se 7. fim-para-todo; saída: T CC/EC/Mestrado Teoria dos Grafos

Complexidade • Os custos relevantes neste algoritmo são o custo da ordenação das arestas (passo 1) e a verificação se a aresta forma um ciclo (passo 4) • Iterativamente o algoritmo forma componentes conexas acíclicas. Então, computar a linha 4 significa verificar se a próxima aresta não liga vértices de um mesmo conjunto. CC/EC/Mestrado Teoria dos Grafos

Complexidade Para a implementação da linha 4 podem ser usadas estruturas de dados para conjuntos disjuntos Usando essa forma de implementação, o algoritmo fica limitado pela complexidade de ordenar a lista de arestas, pois a operação de verificar se é acíclico fica mais barata. Assim teremos O(m*log m). Se |E| < |V|2, teremos O(m*log n) CC/EC/Mestrado Teoria dos Grafos

Algoritmo de Prim entrada: G = (V, E), Lista de Adjacência de G: A(v), v V, matriz de pesos 1. T ← ; 2. V´ ← {u}; 3. para-todo v V – V´ faça 4. L(v) ← peso ({u, v}); 5. fim-para-todo 6. enquanto V´ V faça 7. ache um vértice w tal que L(w) = min {L(v)| v V-V´}; 8. u = o vértice de V´, ligado a w, representando a aresta com o menor custo; 9. e = {u, w}; 10. T ← T U {e}; 11. V´← V´ U {w}; 12. para-todo v V – V´ faça 13. se peso({v, w}) < L(v) então 14. L(v) ← p({v, w}); 15. fim-se 16. fim-para-todo 17. fim-enquanto saída: T CC/EC/Mestrado Teoria dos Grafos

Complexidade • Linhas 6 - 16: n-1 vezes • Linhas 7 - 8: n-1 vezes • Linhas 11 – 15: n-1 vezes • Complexidade: O(n 2) CC/EC/Mestrado Teoria dos Grafos

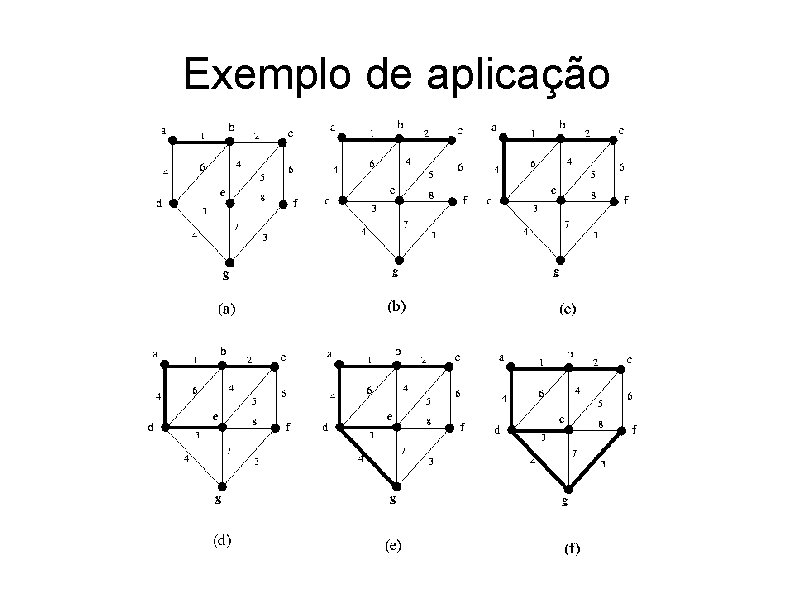
Exemplo de aplicação