A TKEKLTSG Tkekltsg a tkepiacrl Tkepiac pnzt cserlnk

A TŐKEKÖLTSÉG

Tőkeköltség a tőkepiacról Tőkepiac: pénzt cserélünk pénzre � Pl. pénzt adok egy vállalatnak valamilyen jövőbeli (várható) kifizetésekért cserébe Az elcserélt pénzek különböznek kockázatosságukban és/vagy időtávjukban Tőkeköltség: a tőke használatának alternatíva költsége ~ azonos kockázatú (és időtávú) tőkepiaci lehetőség várható hozama Várható hozam és kockázat kapcsolata a tőkepiacon: tőkepiaci árfolyamok modellje (Capital Asset Pricing Model, CAPM) – célunk most ennek levezetése…

Várható hasznosság maximalizálása Emlékezzünk: racionalitás: várható hasznosság maximalizálása Matematikai várható érték vs. várható hasznosság Minket nem a vagyon (pénz) érdekel önmagában, hanem a hozzá tartozó hasznosság! Miért más a két célfüggvény?

Csökkenő határhasznosság elve Egy újabb egységnyi vagyonnövekedésre eső hasznosság egyre kisebb…

Kockázatkerülés A csökkenő határhasznosságból fakad A matematikailag „fair” eset elutasítása � Példa: 50% valószínűséggel nyerhetünk, illetve veszthetünk 1 millió Ft-ot – miért nem vágunk bele? Vagyonunk ugyan várhatóan + 0, 5*(W 0 -1) = W 0, de: nem változik: E(W) = 0, 5*(W 0+1) 1 millió Ft megnyerése kisebb öröm, mint amekkora fájdalom 1 millió Ft elvesztése Matekosan: E(U(W)) = 0, 5*U(W 0+1) + 0, 5*U(W 0 -1) < U(W 0) Azaz ha belevágunk, hasznosságunk várhatóan csökken! Minél „görbültebb” a hasznosságfüggvény, annál inkább kockázatkerülő

Hozamok és kockázatkerülés (I. ) Vagyon ~ pénzösszeg ~ hozam: jellegükben ugyanazok az összefüggések megmaradnak � Ezentúl a hozammal foglalkozunk Hozam – valószínűségi változó � Sok, egymástól független véletlen hatás eredőjeként alakul → normális eloszlásúnak feltételezhetjük � Így két paraméterrel definiálható: E(r) várható érték és σ(r) szórás � A kockázatot matematikailag a szórással ragadjuk meg Tegyük az eddigieket egy modellbe!

Hozamok és kockázatkerülés (II. ) Azonos várható hasznosságot jelentő hozamok (egy adott, kockázatkerülő befektetőre): r. A E(r. C) E(r. B) E(r. D) r

Hozamok és kockázatkerülés (III. ) Egy közömbösségi görbe:

Hozamok és kockázatkerülés (IV. ) Várható hozam – szórás preferencia-térkép két eltérő kockázatkerülésű befektetőre:

Hozamok és kockázatkerülés (V. ) Várható hozam – szórás kapcsolat analitikusan (közelítő formula): A: kockázatkerülési együttható A kockázatot a matematikai szórással azonosítjuk A hozamokat normális eloszlásúnak feltételezzük Kockázatkerülést tételezünk fel

Hatékony portfóliók tartása (I. ) Láttuk: egy befektetésnek van valamilyen várható hozama és kockázata Csökkenthető-e a kockázat úgy, hogy a várható hozam nem változik? � Ha igen, és költségmentesen, akkor nyilván élni fogok ezzel a lehetősséggel Modern portfólió-elmélet (Modern Portfolio Theory, MPT) � Harry Markowitz, ’ 50 -es évek, később Nobel-díj Portfólió: befektetésekből álló „csomag”

Hatékony portfóliók tartása (II. ) Kombináljuk a különféle befektetési lehetőségeket! Diverzifikáció: a tőkénk megosztása több befektetési lehetőség között (~portfólió kialakítása) A portfólió nem szimplán csak az egyedi befektetések összessége �A várható hozama nem, viszont a szórása függ az egyes elemek közötti sztochasztikus kapcsolatoktól! Normális eloszlás, E(ri), σ(ri)

Hatékony portfóliók tartása (III. ) Egy n elemből álló P portfólió várható hozama: A portfólió szórása:

Hatékony portfóliók tartása (IV. ) Nézzük meg n=2 -re: És n=3 -ra is:

Hatékony portfóliók tartása (V. ) Tetszőleges n elemszámú portfólió – mi van, ha minden korreláció 1 (teljes függőség van)? A portfólió szórása ekkor tehát az elemek szórásainak súlyozott átlaga

Hatékony portfóliók tartása (VI. ) Ugyanez, csak n db egyformán „átlagos” szórású elemre: Természetesen ugyanazt kaptuk, mint előbb

Hatékony portfóliók tartása (VII. ) Nézzük, mi van, ha minden páronkénti korreláció 0! Tekintsünk most is n db egyformán „átlagos” szórású elemet!

Hatékony portfóliók tartása (VIII. ) Mi van akkor, ha n → ∞ ?

Hatékony portfóliók tartása (IX. ) Ha van negatív korrelációjú tag, akkor kevesebb elemszám esetén is nulla lehet a portfólió szórása � Akár már két elem is elegendő lehet Ha minden tag 0 és 1 közötti korrelációjú, akkor csökken a szórás, de nem nulláig Ha mindenféle korreláció előfordul, akkor lehet nulla, de ha többségében pozitív kapcsolat, akkor valamilyen pozitív értékig csökken csak (a szórás negatív nem lehet!) Általános szabály: ha nincs teljes függőség, akkor nagyobb elemszám → kisebb szórás, és minél kisebb korrelációk, annál „gyorsabban” Cél: úgy kombinálni a befektetési lehetőségeket, hogy minél nagyobb várható hozamhoz minél kisebb szórás

Hatékony portfóliók tartása (X. ) Példa: Részvény Danubius (i) Pannonplast (j) Várható hozam (%) 2, 5 3, 3 Szórás (%) 11, 4 17, 1

Hatékony portfóliók tartása (XI. ) Ábrázoljuk a lehetséges portfóliókat különféle korrelációk esetén: A korrelációk persze a valóságban adottak…

Hatékony portfóliók tartása (XII. ) Nézzük meg a három különböző elemből összeállítható portfóliókat (feltüntetve a páronként lehetséges portfóliókat is): Látható, hogy a három befektetési lehetőséggel együtt érhető el a legnagyobb szóráscsökkenés…

Hatékony portfóliók tartása (XIII. ) Nézzük meg a „világ összes” kockázatos befektetési lehetőségét: Hatékony portfóliók Az adott befektetőnek a B pont maximalizálja a hasznosságát Feltételezések: 1) nincsenek szélsőséges hozam-szórás párok, 2) egy adott kockázati szint alatt nincs lehetőség, 3) a szórás nem csökkenthető nulláig

Hatékony portfóliók tartása (XIV. ) Hatékony portfólió: adott várható hozamnál a legkisebb kockázatot, ill. adott kockázatnál a legnagyobb várható hozamot adja (nem diverzifikálható tovább) A kockázat alakulása a diverzifikáltság mértékével:

Hatékony portfóliók tartása (XV. ) A különböző preferenciájú befektetők választása: A kockázatkerülési együtthatójuktól függ, hogy melyik hatékony portfóliót választják

Hatékony portfóliók tartása (XVI. ) A Markowitz-féle modell problémái � Egy befektetésnek az összes többi befektetéssel való korrelációs kapcsolatát ismerni kell �A tartott hatékony portfóliók befektetőnként eltérőek → egy-egy befektetés ténylegesen érzékelt kockázata befektetőnként eltérő A modell gyakorlati alkalmazása „szinte reménytelen”

Portfólió-választás példa (I. ) Adott két befektetési lehetőség: � i: E(ri) = 12%, σ(ri) = 15% � j: E(rj) = 7%, σ(rj) = 9% � ki, j = 0, 3 Mekkora az ezen két elemből összeállított portfólió várható hozama és szórása, ha � I. : ai = 0, 2 és aj = 0, 8 � II. : ai = 0, 8 és aj = 0, 2 Az I. és a II. portfólió közül melyiket választaná egy A=2, illetve egy A=8 kockázatkerülésű befektető? Ábrázoljuk grafikusan is! (csak jelleghelyesen)

Portfólió-választás példa (II. ) Megoldás I. portfólió: � E(r. P) = 0, 2*0, 12 + 0, 8*0, 07 = 0, 08 = 8% � σ(r. P) = [(0, 2*0, 15)2 + (0, 8*0, 09)2 + 2*0, 3*0, 2*0, 15*0, 8*0, 09]1/2 = 0, 0859 = 8, 59% II. portfólió: � E(r. P) � σ(r. P) = 0, 8*0, 12 + 0, 2*0, 07 = 0, 11 = 11% = [(0, 8*0, 15)2 + (0, 2*0, 09)2 + 2*0, 3*0, 8*0, 15*0, 2*0, 09]1/2 = 0, 1266 = 12, 66%

Portfólió-választás példa (III. ) Portfóliók várható hasznossága, ha A=2: � I. portfólió: U = 0, 08 – 0, 5*2*0, 112 = 0, 0726 � II. portfólió: U = 0, 11 – 0, 5*2*0, 12662 = 0, 0940 � Mivel UII > UI, ezért a II. portfóliót választaná Portfóliók várható hasznossága, ha A=8: � I. portfólió: U = 0, 08 – 0, 5*8*0, 112 = 0, 0505 � II. portfólió: U = 0, 11 – 0, 5*8*0, 12662 = 0, 0459 � Mivel UI > UII, ezért az I. portfóliót választaná

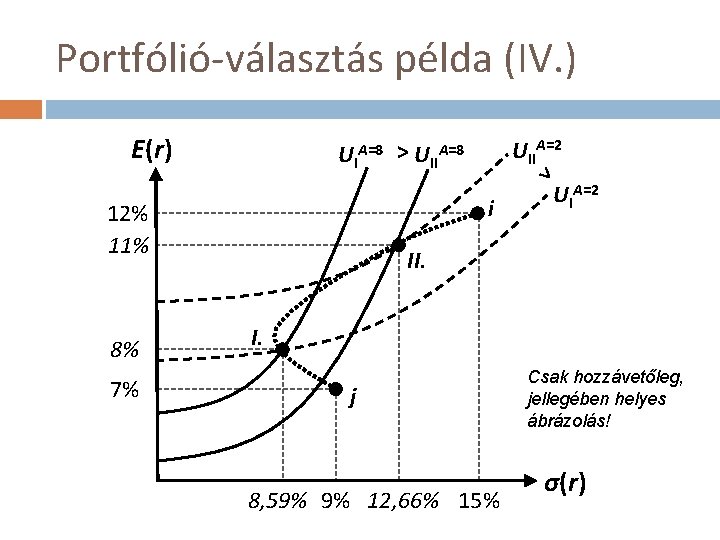
Portfólió-választás példa (IV. ) E(r) UIA=8 > UIIA=8 i 12% 11% 8% 7% UIIA=2 > UIA=2 II. I. j 8, 59% 9% 12, 66% 15% Csak hozzávetőleg, jellegében helyes ábrázolás! σ(r)

Portfólió-választás példa (V. ) Gyakorlásra: Kétféle portfólió 3 db elemből: E(r) σ(r) I. II. i 10% 20% 0, 4 0, 2 j 8% 12% 0, 2 z 5% 5% 0, 4 0, 6 Korrelációk: ki, j = -0, 2; ki, z = 0, 7; kj, z = 0, 5 Az I. vagy II. portfóliót választaná egy A=8 befektető? (Megoldás: a II. -t, mert UII = 0, 0456 > UI = 0, 0387, mivel I. -re E(r. P) = 7, 60% és σ(r. P) = 9, 66%, és II. -re E(r. P) = 6, 60% és σ(r. P) = 7, 14%)

Portfólió-választás példa (VI. ) Csak akit jobban érdekel a téma, és szeret számolni: Előző kételemű példához: � i-hez és j-hez önmagában tartozó hasznosságok � Legkisebb szórású portfólió meghatározása � Legnagyobb hasznosságú portfólió meghatározása � (Utóbbi kettőhöz az ötlet: aj = 1 – ai, majd egyváltozós szélsőérték feladat) � Aki rajzolni is szeret: pontosabb grafikus ábrázolás a fentiek ismeretében…