7 7 Hinge Theorem Proof Geometry Hinge Theorem

7 -7: Hinge Theorem Proof Geometry

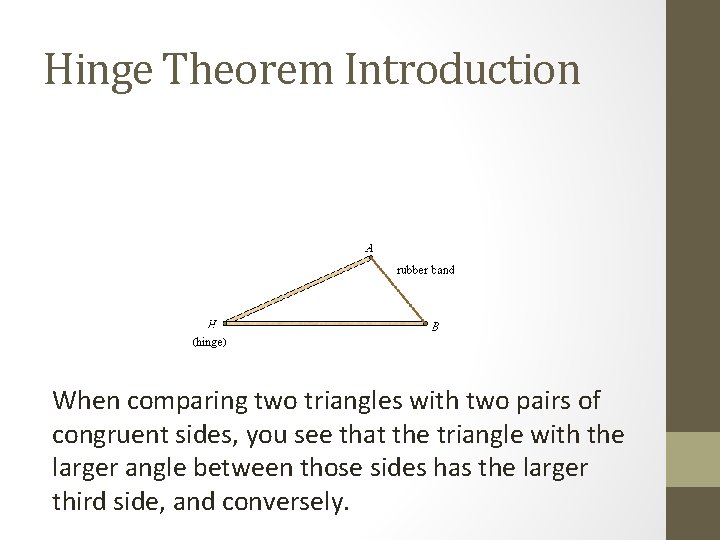
Hinge Theorem Introduction When comparing two triangles with two pairs of congruent sides, you see that the triangle with the larger angle between those sides has the larger third side, and conversely.

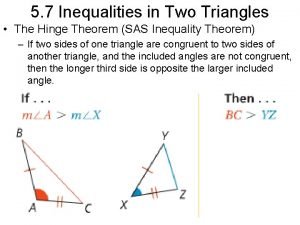
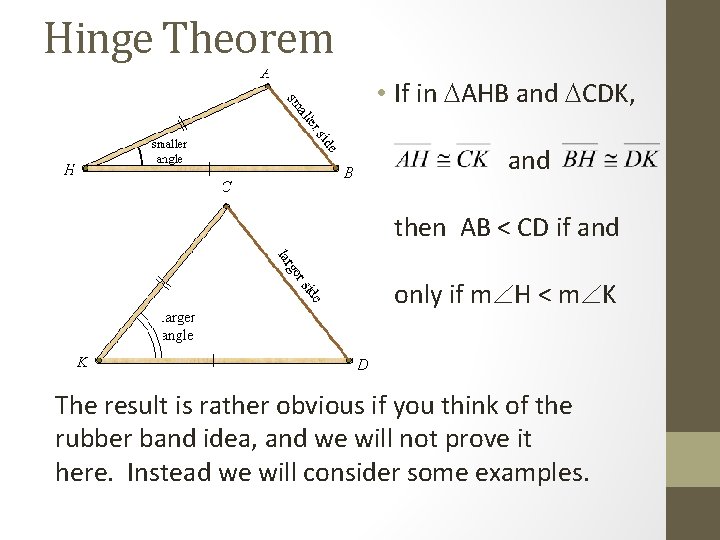
Hinge Theorem • If in AHB and CDK, and then AB < CD if and only if m H < m K The result is rather obvious if you think of the rubber band idea, and we will not prove it here. Instead we will consider some examples.

Example 1 • 1. AC = AB 2. AD = AD 3. m CAD < m DAB 4. CD < BD Given Reflexive Given Hinge Theorem

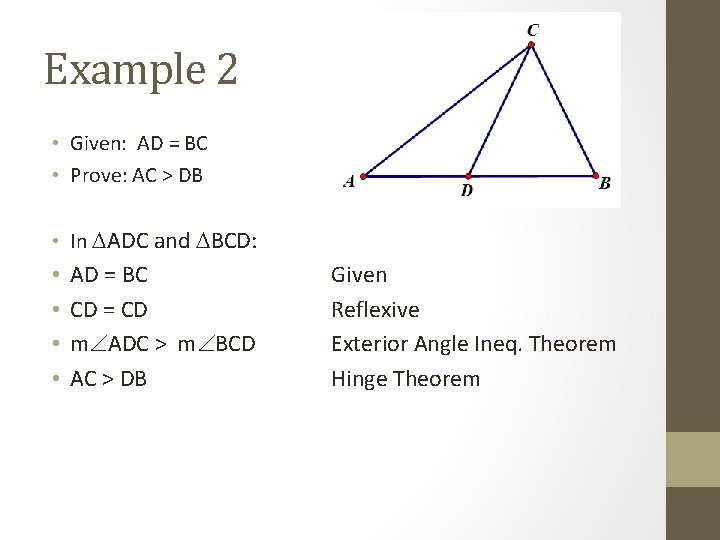
Example 2 • Given: AD = BC • Prove: AC > DB • In ADC and BCD: • • AD = BC CD = CD m ADC > m BCD AC > DB Given Reflexive Exterior Angle Ineq. Theorem Hinge Theorem

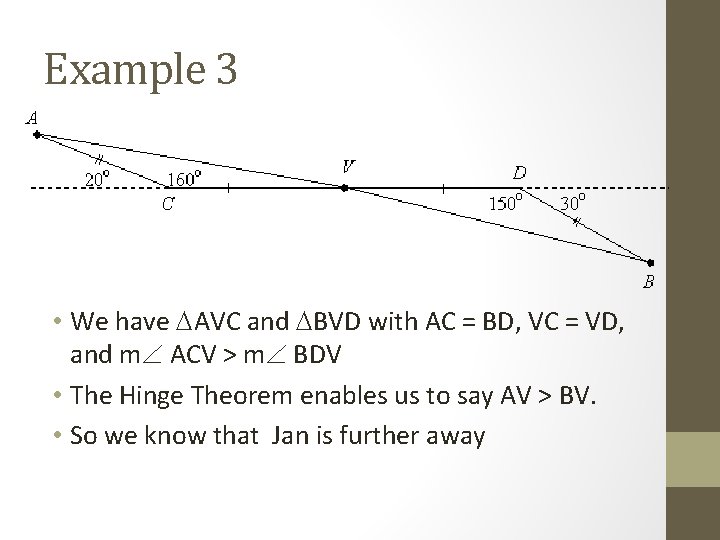
Example 3 • Jan and Jon are hikers. They start at the visitor center and walk in opposite directions for 2 miles. Then Jan turns to her right at an angle of 20 o, and Jon turns to his right at an angle of 30 o. They each continue hiking for another mile and a half when both stop to rest. Who is farther (as the crow flies) from the visitor center?

Example 3 • We have AVC and BVD with AC = BD, VC = VD, and m ACV > m BDV • The Hinge Theorem enables us to say AV > BV. • So we know that Jan is further away

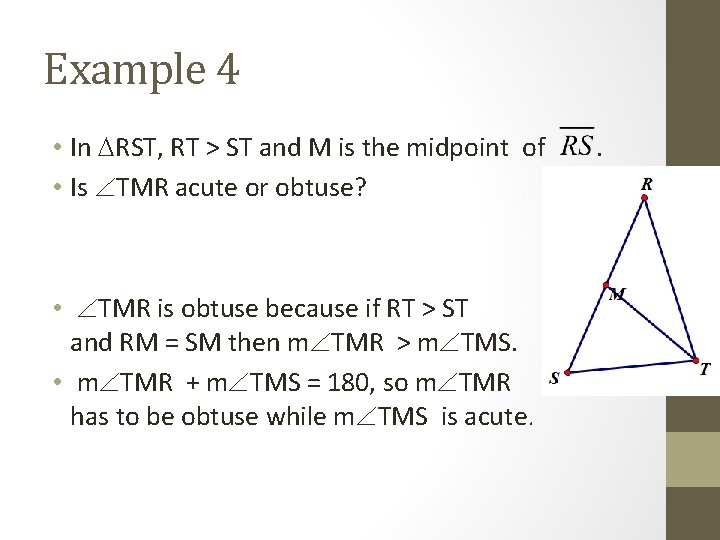
Example 4 • In RST, RT > ST and M is the midpoint of • Is TMR acute or obtuse? • TMR is obtuse because if RT > ST and RM = SM then m TMR > m TMS. • m TMR + m TMS = 180, so m TMR has to be obtuse while m TMS is acute. .

Homework p. 234 -236: #1 -3, 6, 10, 11, 15