5 VGTELEN HALMAZOK 1 5 1 Kivlasztsi axima

5. VÉGTELEN HALMAZOK 1 5. 1 Kiválasztási axióma Másképp: nemüres halmazok bármely családjának a szorzata nem üres.

Def Rövidítés: B majorálja A-t. Ha B majorálja A-t, de nem ekvivalensek, akkor B szigorúan majorálja A-t. Példa: Legyen B: = Z, A: = 2 Z (páros számok halmaza). B A, mert : B A, (x) : = 2 x, bijekció, és 2

Kérdések: 3 trivi igaz, nem biz. Schröder-Bernstein-tétel Cantor-tétel

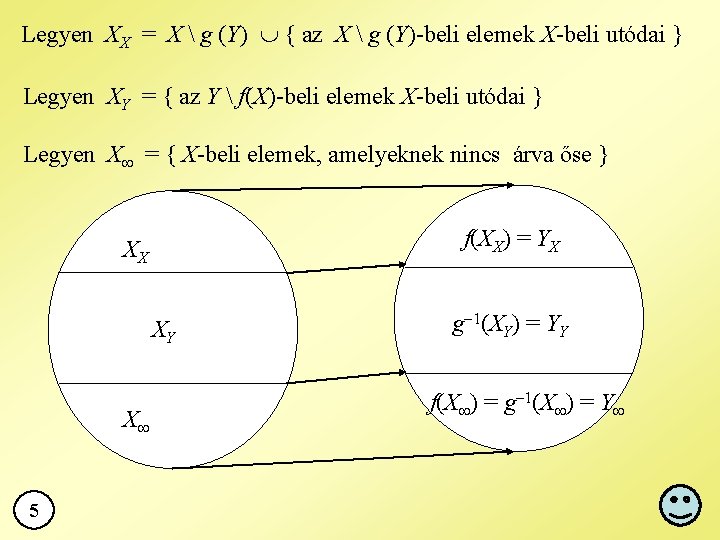
Schröder-Bernstein-tétel: Biz. Feltehetjük, hogy X, Y diszjunkt halmazok és legyen f: X Y, g: Y X injektív függvény. Utódok (ősök) sorozata: x X esetén f(x), g(f(x)), f(g(f(x))), … árvába torkollik végtelen „Árva” : olyan X g (Y) vagy Y f(X) beli elem, amelynek nincs „őse” a másik halmazban. 4

Legyen XX = X g (Y) { az X g (Y)-beli elemek X-beli utódai } Legyen XY = { az Y f(X)-beli elemek X-beli utódai } Legyen X = { X-beli elemek, amelyeknek nincs árva őse } f(XX) = YX XX XY X 5 g 1(XY) = YY f(X ) = g 1(X ) = Y

5. 1. 11. 6 5. 1. 12. Biz. f bijektív és y X : f(y) = Y y Y = f(y)

5. 2 Megszámlálható halmazok 7

Biz. Ha X véges X nem lehet végtelen, mert lenne 8 többi trivi

Biz. 9

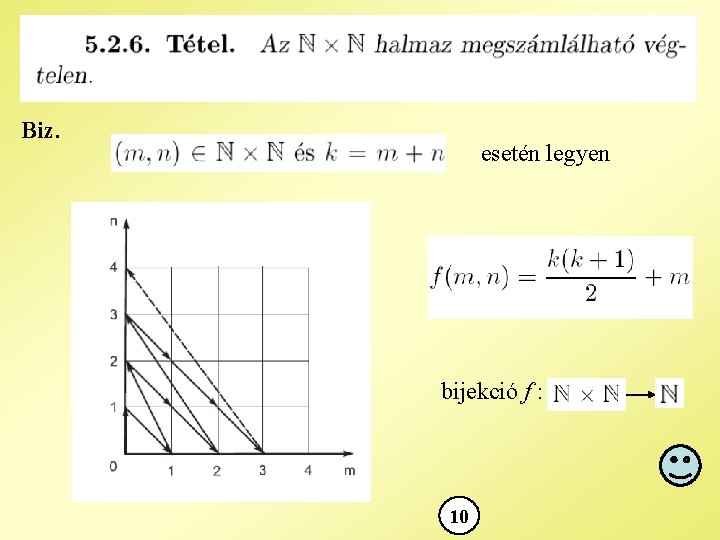
Biz. esetén legyen bijekció f : 10

Biz. A = A 1 A 2 … Diszjunkt halmazokat csinálunk: A 1’ = A 1 , A 2’ = A 2 A 1’ , A 3’ = A 3 (A 1’ A 2’). . . 11

12 Ai’ halmazokra igaz: 1. Ai’ Ai i -re. 2. A = A 1’ A 2’ . . 3. Ai’ Aj’ = olyan i, j esetén, ahol i j. Feltétel Ai’ halmazok sorbarendezhetők : A 1’ = { a 11, a 12, a 13, . . . }, A 2’ = { a 21, a 22, a 23, . . . }, A 3’ = { a 31, a 32, a 33, . . . },

Biz. Z = N+ {0} N 5. 2. 6 Tétel 13 megszámlálható is

Biz. diszjunktság miatt helyettesítsük X-et X Y-nal Legyen Z Y megszámlálható végtelen, f : Z X Z bijekció, és g : Y X Y bijekció ! 14

Biz. Tfh Y véges 4. fejezet nem lehet ekvivalens saját valódi részhalmazával Tfh Y végtelen, x Y , és legyen Z = { x }, X = Y Z Y=X Z ~X végtelen 15 megszámlálható tétel

5. 3 Nem megszámlálható halmazok Biz. 16

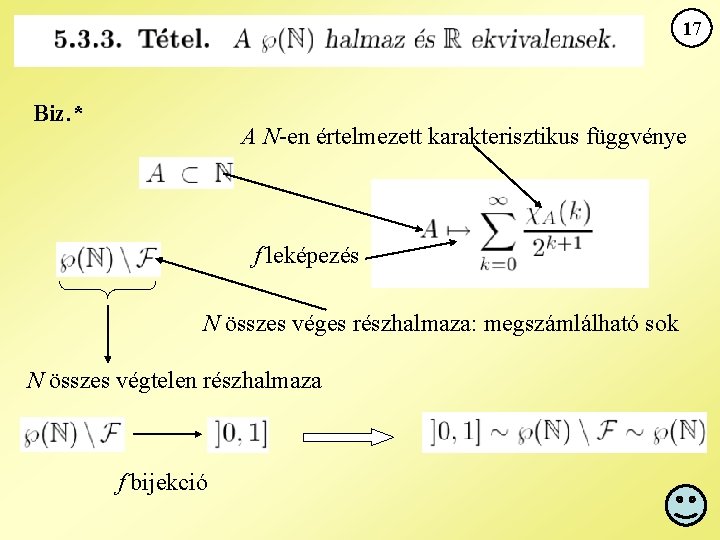
17 Biz. * A N-en értelmezett karakterisztikus függvénye f leképezés N összes véges részhalmaza: megszámlálható sok N összes végtelen részhalmaza f bijekció

Lemma. Biz. nem megszámlálható számosságú. Előzőekből tudjuk: (0, 1) [0, 1) [0, 1] R. Legyen A = {x x R, 0 x < 1}. Probléma: a szokásos módon nem tudjuk leírni a 0 egészrészű számokat: 0, 199999999. . . 0, 200000000. . . vizsgálatunk tárgya: 18 B = {x x 0 -val kezdődő tizedestört, és nem tartalmaz valamely helytől kezdve csupa 9 -est}.

Próbáljuk meg B halmazt sorbarendezni ! x 1 = 0, a 11 a 12 a 13. . . x 2 = 0, a 21 a 22 a 23. . . x 3 = 0, a 31 a 32 a 33. . . y = 0, b 1 b 2 b 3. . . bk akk, bk [0. . 8]. y [0, 1) és y B , de y xi ! 19

Biz. =X megszámlálható végtelen 20

Kontinuumhipotézis: 21 Nem létezik olyan X halmaz, amire N (N). X Általánosított kontinuumhipotézis: Tetszőleges Y halmazra nem létezik olyan X halmaz, amire Y X (Y). Válasz: ZFC-ben egyik sem cáfolható és egyik sem bebizonyítható! Gödel 1939 Cohen 1963