1 Identification de la sollicitation en traction Une

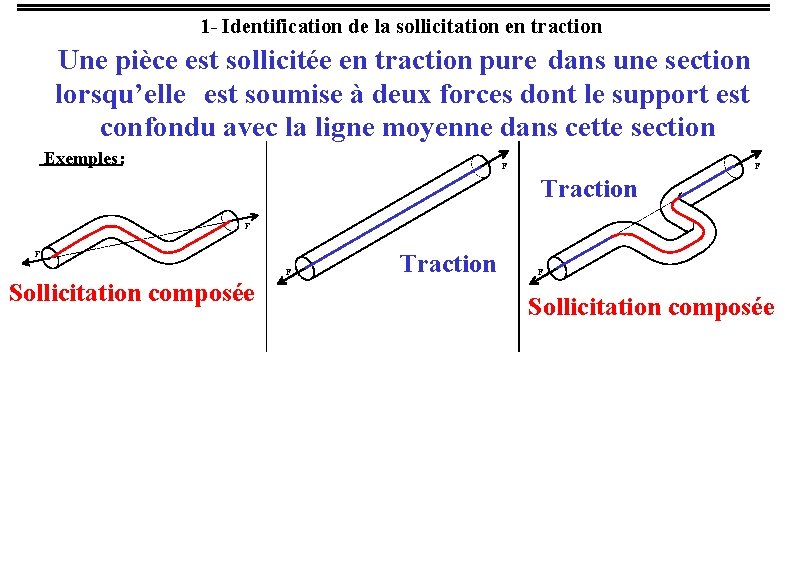
1 - Identification de la sollicitation en traction Une pièce est sollicitée en traction pure dans une section lorsqu’elle est soumise à deux forces dont le support est confondu avec la ligne moyenne dans cette section Exemples : F F Traction F F F Sollicitation composée Traction F Sollicitation composée

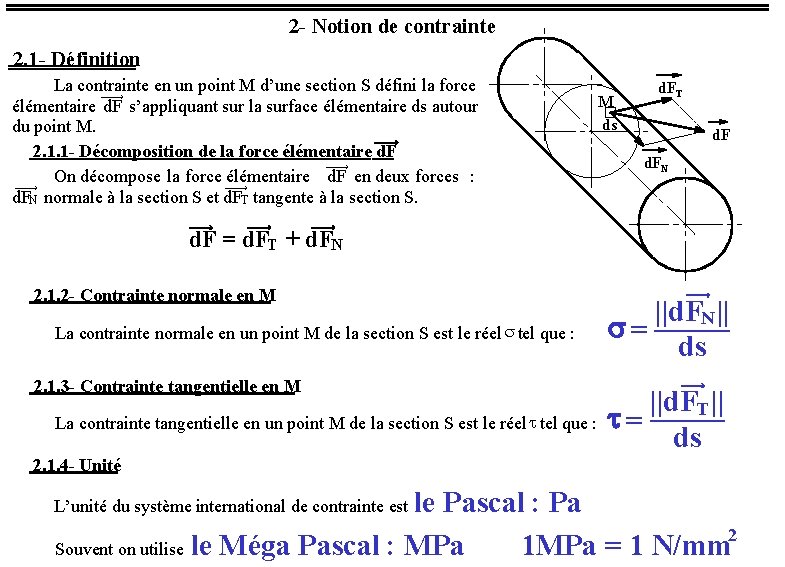
2 - Notion de contrainte 2. 1 - Définition La contrainte en un point M d’une section S défini la force ¾¾® élémentaire d. F s’appliquant sur la surface élémentaire ds autour du point M. ¾¾® 2. 1. 1 - Décomposition de la force élémentaire d. F ¾¾® On décompose la force élémentaire d. F en deux forces : ¾¾® d. FN normale à la section S et d. FT tangente à la section S. ¾¾® M ds d. FT d. FN ¾¾® d. F = d. FT + d. FN 2. 1. 2 - Contrainte normale en M La contrainte normale en un point M de la section S est le réel s tel que : 2. 1. 3 - Contrainte tangentielle en M La contrainte tangentielle en un point M de la section S est le réel t tel que : ¾¾® ||d. FN || s= ds ¾¾® ||d. FT || t= ds 2. 1. 4 - Unité le Pascal : Pa Souvent on utilise le Méga Pascal : MPa 1 MPa = 1 N/mm 2 L’unité du système international de contrainte est

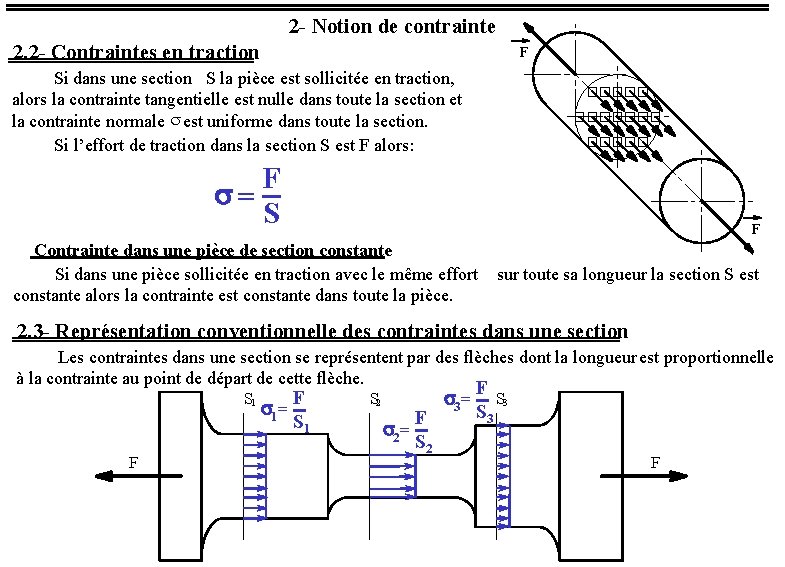
2 - Notion de contrainte 2. 2 - Contraintes en traction F Si dans une section S la pièce est sollicitée en traction, alors la contrainte tangentielle est nulle dans toute la section et la contrainte normale s est uniforme dans toute la section. Si l’effort de traction dans la section S est F alors : F s= S F Contrainte dans une pièce de section constante Si dans une pièce sollicitée en traction avec le même effort constante alors la contrainte est constante dans toute la pièce. sur toute sa longueur la section S est 2. 3 - Représentation conventionnelle des contraintes dans une section Les contraintes dans une section se représentent par des flèches dont la longueur est proportionnelle à la contrainte au point de départ de cette flèche. S 1 F F s 1= S 1 S 2 s 2= F S 2 s 3= F S 3 F

4 - Condition de résistance d’une pièce Soit une pièce constituée d’un matériau de limite élastique Re et de résistance à la rupture Rr. On suppose que cette pièce est une poutre sollicitée en traction sur toute sa longueur. Elle est donc soumise à deux forces directement opposées de module F et de support la ligne moyenne de la poutre. (Cette ligne moyenne est donc une droite). La pièce résiste si la contrainte smax reste inférieure à la contrainte maximale admissible sadm : smax < sadm RPe Re = s Avec : sadm = Limite pratique élastique Où : sadm ( s : coefficient de sécurité ) 4. 1 - Cas où la section est constante. Si la section de cette pièce est constante alors la contrainte est constante dans toute la pièce (Excepté près des endroits où sont appliqués les deux forces de traction de cette pièce). On a donc : smax = F S où S est l’aire de la section de la pièce.

4 - Condition de résistance d’une pièce Soit une pièce constituée d’un matériau de limite élastique Re et de résistance à la rupture Rr. On suppose que cette pièce est une poutre sollicitée en traction sur toute sa longueur. Elle est donc soumise à deux forces directement opposées de module F et de support la ligne moyenne de la poutre. (Cette ligne moyenne est donc une droite). La pièce résiste si la contrainte smax reste inférieure à la contrainte maximale admissible sadm : smax < sadm RPe Re = s Avec : sadm = Limite pratique élastique Où : sadm ( s : coefficient de sécurité ) 4. 2 - Cas où la section n’est pas constante Dans ce cas la contrainte est variable et sa valeur dans une section i d’aire Si est : si = F Si Par conséquent il faut calculer la contrainte maximale dans cette pièce, laquelle se situe dans la section la plus petite: Smin. On a donc : smax = F Smin. où Smin est l’aire de la plus petite section de la pièce.

5 - Loi de Hooke : Déformation de la pièce 5. 1 - Cas où la section est constante. Soit une pièce constituée d’un matériau de limite élas tique Re et de module d’Young E. La loi de Hooke qui est valable dans la zone élastique ( smax £ Re ) permet d’écrire que : s= E. e Avec : DL e= L 0 On a donc : s DL = L 0 E L’allongement DL d’une pièce sollicitée en traction sur toute sa longueur L 0 est donc : s DL = L 0 E

5 - Loi de Hooke : Déformation de la pièce 5. 2 - Cas où la section n’est pas constante. ( Poutre avec plusieurs sections d’aire Si ) DL = S Li. si E Où : si est la contrainte dans la section Si et Li la longueur de section Si. Exemple S 1 S 2 S 3 F F L 1 L 2 L 3 s 1 s 2 s 3 F F F DL = L 1 + L 2 + L 3 E E E S 1. E S 2. E S 3. E æ ç ç è ö L L L F 1 2 3÷ DL = + + ÷ E S 1 S 2 S 3 ø