Wykad 24 20 Fale elektromagnetyczne 20 1 Rwnanie

Wykład 24 20. Fale elektromagnetyczne 20. 1 Równanie falowe 20. 2 Doświadczenie Herza - drgający dipol elektryczny 20. 3 Rozchodzenie się fal elektromagnetycznych w przewodnikach Reinhard Kulessa 1

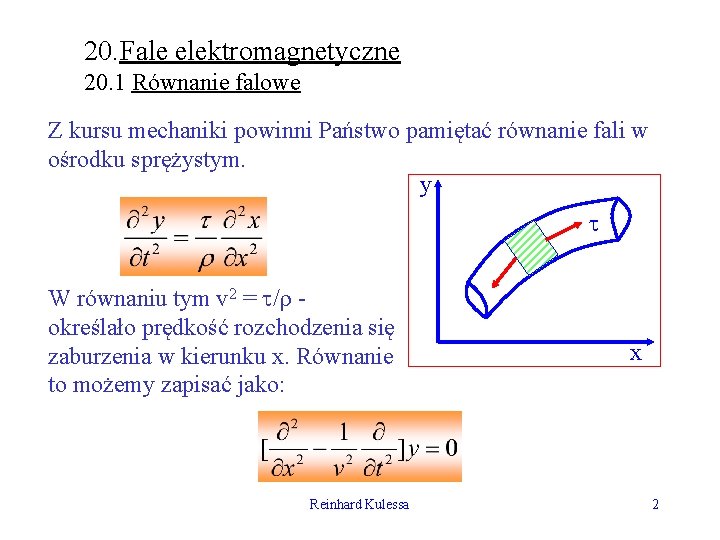
20. Fale elektromagnetyczne 20. 1 Równanie falowe Z kursu mechaniki powinni Państwo pamiętać równanie fali w ośrodku sprężystym. y W równaniu tym v 2 = / określało prędkość rozchodzenia się zaburzenia w kierunku x. Równanie to możemy zapisać jako: Reinhard Kulessa x 2

Równanie to poza tym, że jest jednorodne, posiada lewą stronę równą tej w równaniu (19. 16) dla potencjałów i A. Widzimy więc, że dla obszaru w którym nie ma ładunków i prądów równanie (19. 16) jest równaniem falowym. Wyprowadźmy sobie więc równanie falowe dla fal elektromagnetycznych wprost z równania Maxwella korzystając z równań materiałowych. Załóżmy, że mamy ośrodek homogeniczny i izotropowy, oraz ze nie zawiera on ładunków. Oznacza to że , , =const. i = 0. Znane nam cztery równania Maxwella mają wtedy w układzie SI następującą postać: Reinhard Kulessa 3

Wykonajmy kolejno zaznaczone po prawej stronie równań I’ i II’ operacje. Otrzymamy wtedy następujące równania. =0 Reinhard Kulessa 4

Eleminując z tych równań wyrażenie oraz mnożąc wynik obustronnie przez 1/ 0 , otrzymujemy: (20. 1) Dla drugiego przypadku eleminując wyrażenie otrzymujemy: (20. 2) Przez kombinację równań Maxwella uzyskaliśmy dwa identycznej postaci równania, które możemy zapisać jako: , Reinhard Kulessa (20. 3) 5

Gdzie może przyjmować wartości H lub E. Równanie to nie jest proste, gdyż występują w nim zarówno pierwsza, jaki i druga pochodna cząstkowa po czasie. Załóżmy, że: . Po podstawieniu otrzymujemy: . (20. 4) Jeśli zajdzie nierówność ( / 0 ) >> , w równaniu dominuje człon z / t i wtedy mamy równanie dyfuzyjne, a gdy ( / 0 ) << , wtedy dominuje człon z 2/ t 2, i otrzymujemy równanie falowe. Dla izolatorów automatycznie jest spełniony warunek dla równania falowego. Widać więc z powyższego, że równania Maxwella zawierają w sobie opis rozchodzenia się fal elektromagnetycznych. Reinhard Kulessa 6

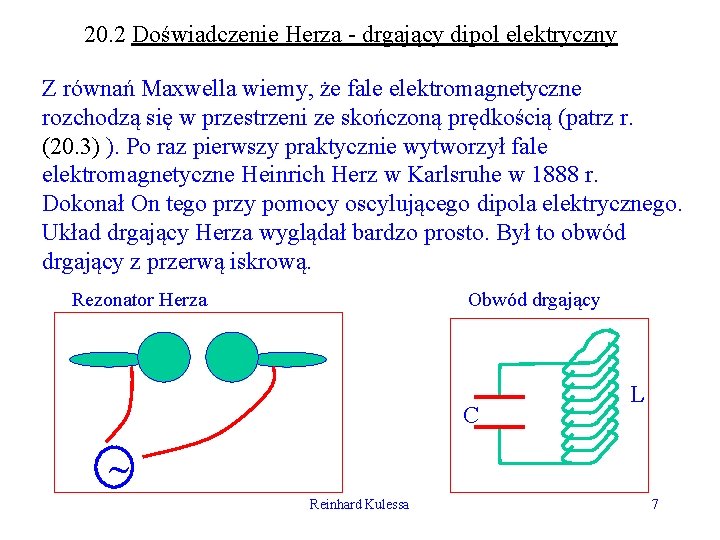
20. 2 Doświadczenie Herza - drgający dipol elektryczny Z równań Maxwella wiemy, że fale elektromagnetyczne rozchodzą się w przestrzeni ze skończoną prędkością (patrz r. (20. 3) ). Po raz pierwszy praktycznie wytworzył fale elektromagnetyczne Heinrich Herz w Karlsruhe w 1888 r. Dokonał On tego przy pomocy oscylującego dipola elektrycznego. Układ drgający Herza wyglądał bardzo prosto. Był to obwód drgający z przerwą iskrową. Rezonator Herza Obwód drgający C L Reinhard Kulessa 7

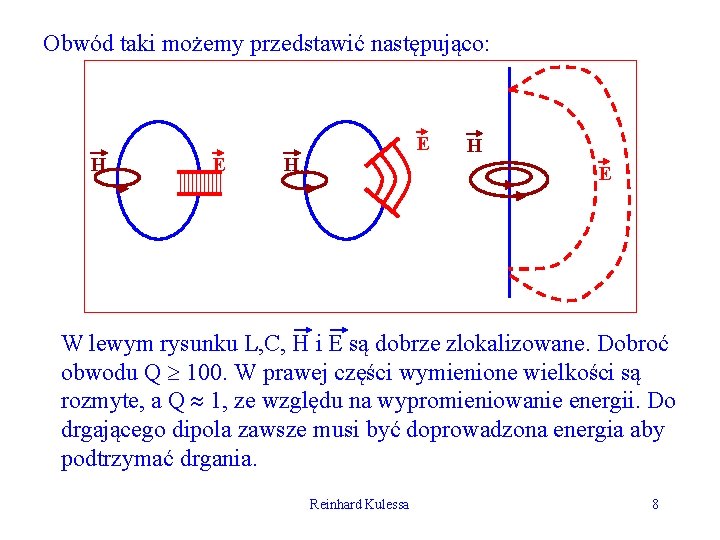
Obwód taki możemy przedstawić następująco: H E E H H E W lewym rysunku L, C, H i E są dobrze zlokalizowane. Dobroć obwodu Q 100. W prawej części wymienione wielkości są rozmyte, a Q 1, ze względu na wypromieniowanie energii. Do drgającego dipola zawsze musi być doprowadzona energia aby podtrzymać drgania. Reinhard Kulessa 8

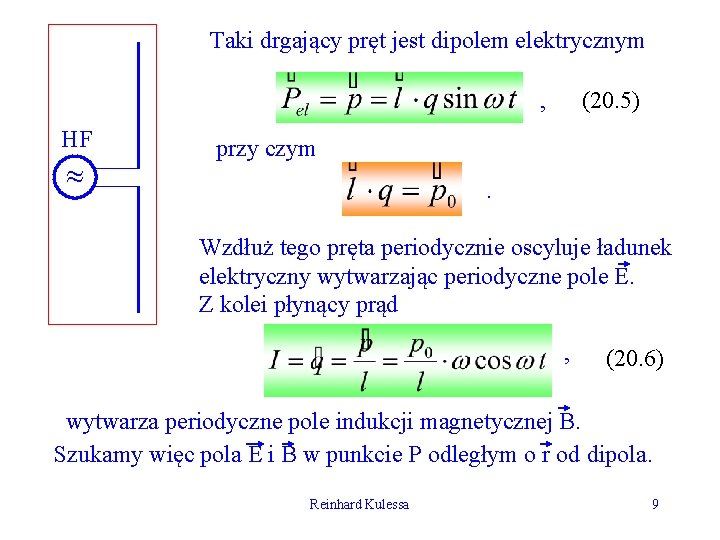
Taki drgający pręt jest dipolem elektrycznym , HF (20. 5) przy czym. Wzdłuż tego pręta periodycznie oscyluje ładunek elektryczny wytwarzając periodyczne pole E. Z kolei płynący prąd , (20. 6) wytwarza periodyczne pole indukcji magnetycznej B. Szukamy więc pola E i B w punkcie P odległym o r od dipola. Reinhard Kulessa 9

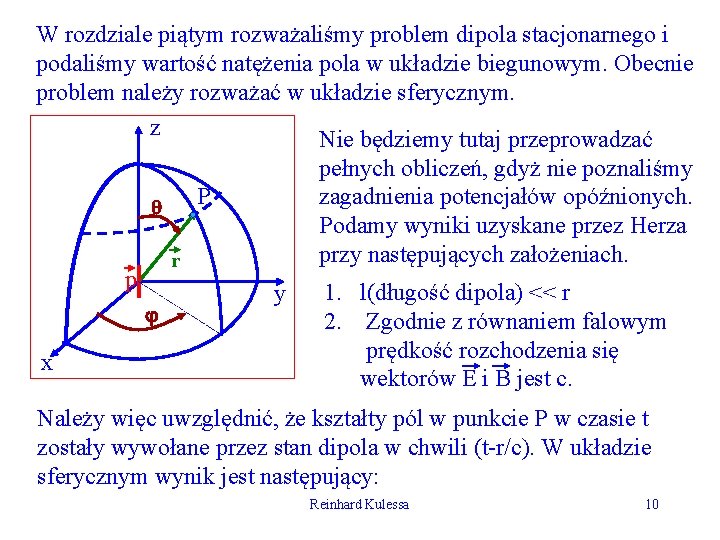
W rozdziale piątym rozważaliśmy problem dipola stacjonarnego i podaliśmy wartość natężenia pola w układzie biegunowym. Obecnie problem należy rozważać w układzie sferycznym. z Nie będziemy tutaj przeprowadzać P r p x pełnych obliczeń, gdyż nie poznaliśmy zagadnienia potencjałów opóźnionych. Podamy wyniki uzyskane przez Herza przy następujących założeniach. y 1. l(długość dipola) << r 2. Zgodnie z równaniem falowym prędkość rozchodzenia się wektorów E i B jest c. Należy więc uwzględnić, że kształty pól w punkcie P w czasie t zostały wywołane przez stan dipola w chwili (t-r/c). W układzie sferycznym wynik jest następujący: Reinhard Kulessa 10

(20. 7) Musimy tu rozważyć dwa przypadki: A). Obszar bliski dipola r << =2 c/. Zarówno prędkość jak i opóźnienia nie grają tu roli. Dla pola E wystąpią te człony, które poznaliśmy w rozdziale 5. 7. 4, czyli podkreślone na powyżej na czerwono. Reinhard Kulessa 11

Dla pola B otrzymamy zgodnie z prawem Biotta-Savarta, Ponieważ wektor indukcji magnetycznej jest prostopadły zarówno do wektora r jak i l, będzie miał tylko składową B. Przypadek ten nie jest związany z rozchodząca się falą elektromagnetyczną. Przejdźmy więc do przypadku drugiego: B) r >> . Zgodnie ze wzorem (20. 5) trzy człony powtarzające się we wzorze (20. 7) można napisać następująco: Reinhard Kulessa 12

. W prawej części równania zastosowaliśmy związek: Ze względu na to, że /r << 1, człony w wyższej potędze będą zaniedbywalne. Dominującą rolę będzie odgrywało więc trzecie równanie. Przybliżone rozwiązanie będzie miało postać: Reinhard Kulessa 13

(20. 8) (20. 9) Wrócimy jeszcze do krótkiego omówienia mocy wypromieniowanej przez dipol później. Reinhard Kulessa 14

20. 3 Rozchodzenie się fal elektromagnetycznych w przewodnikach Rozważmy koaksialny przewód z dwóch rur, w których płyną prądy I w przeciwnych kierunkach. Skorzystajmy w tym celu ze znanego nam już rysunku Jeśli pomiędzy przewodami zakreślimy pętlę o promieniu r, to zgodnie z prawem Ampera : 2 b 2 a x V(x B(r) 0 +x I ) r I V(x 0) Reinhard Kulessa 15

Wobec tego Dla a < r < b. Strumień indukcji magnetycznej przez zakreskowana powierzchnię wynosi: . Wobec tego współczynnik indukcji własnej na jednostkę długości kabla wynosi: . (20. 10) Równocześnie pojemność kondensatora cylindrycznego wynosi: Reinhard Kulessa 16

(20. 11) Mamy więc, że; (20. 12) Równanie to jest słuszne dla wszystkich rodzajów podwójnych kabli. Widzimy więc, ze rozchodzą się po nich fale elektromagnetyczne. Reinhard Kulessa 17