Warm up 2 2 2 2 Definitions and

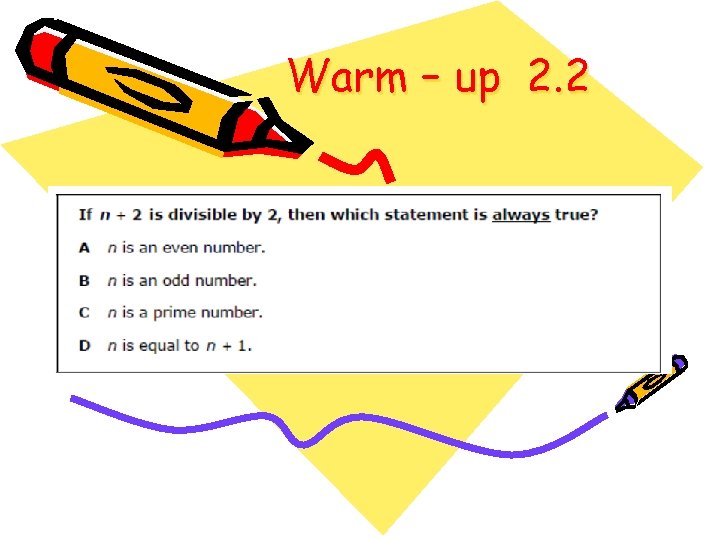
Warm – up 2. 2

2. 2 Definitions and Biconditional Statements Geometry Gonzales

Standard/Objectives Standard 1. 2: Conditional Statements. Objectives: • Recognize and use definitions. • Recognize and use biconditional statements.

Definitions • perpendicular lines – • are those which intersect if they form a right angle A line perpendicular to a plane is a line that intersects the plane in a point and is perpendicular to every line in the plane that intersects it.

Recognizing and using definitions • All definitions can be interpreted “forward” and “backward. ” The definition of perpendicular lines means • – – If two lines are perpendicular, then they intersect to form a right angle, and If two lines intersect to to form a right angle, then they are perpendicular.

Example 1 • Decide whether each statement about the diagram is true. Explain your answers. x a. Points D and B are collinear. b. AC is perpendicular to DB. c. Angle AXB is adjacent to and CXD.

Example 1 • Decide whether each statement about the diagram is true. Explain your answers. a. True. Two points are collinear if they lie on the same point. b. True. The right angle symbol in the diagram indicates that lines AC and DB intersect to form a right angle; so the lines are perpendicular. c. False. By definition, adjacent angles must share a common side. They do not, so are not adjacent.

Using Biconditional Statements n n n Conditional statements are not always written in the if-then form. Another common form of a conditional is only-if form. Here is an example. It is Saturday (hypothesis), only if I am working at the restaurant (conclusion). You can rewrite this conditional statement in if-then form as follows: If it is Saturday, then I am working at the restaurant. A biconditional statement is one that contains the phrase “if and only if. ” Writing a biconditional statement is equivalent to writing a conditional statement and its converse.

Example 2 n n The biconditional statement below can be rewritten as a conditional statement and its converse. Three lines are coplanar if and only if they lie in the same plane. Conditional statement: If three lines are coplanar, then they lie in the same plane. Converse: If three lines lie in the same plane, then they are coplanar.

Biconditional Statements • A biconditional statement can either be true or false. To be true, BOTH the conditional statement and its converse must be true. This means that a true biconditional statement is true both “forward” and “backward. ” All definitions can be written as true biconditional statements.

Example 3: Analyzing Biconditional Statements • Consider the following statement: x = 3 if and only if x 2 = 9. Is this a biconditional statement? • – • The statement is biconditional because it contains the phrase “if and only if. ” Is the statement true? – – Conditional statement: If x = 3, then x 2 = 9. Converse: x 2 = 9, then x = 3. • The first part of the statement is true, but what about -3? That makes the second part of the statement false.

Example 4: Writing a Biconditional Statement • Each of the following is true. Write the converse if each statement and decide whether the converse is true or false. If the converse is TRUE, then combine it with the original statement to form a true biconditional statement. If the statement is FALSE, then state a counterexample. – If two points lie in a plane, then the line containing them lies in the plane.

Example 4: Writing a Biconditional Statement • • Converse: If a line containing two points lies in a plane, then the points lie in the plane. The converse is true as shown in the diagram on page 81. It can be combined with the original statement to form a true biconditional statement written below: Biconditional statement: Two points lie in a plane if and only if the line containing them lies in the plane.

Example 4: Writing a Biconditional Statement • • B. If a number ends in 0, then the number is divisible by 5. Converse: If a number is divisible by 5; then the number ends in 0. The converse isn’t true. What about 25? Knowing how to use true biconditional statements is an important tool for reasoning in Geometry. For instance, if you can write a true biconditional statement, then you can use the conditional statement or the converse to justify an argument.

Example 5: Writing a Postulate as a Biconditional Statement • • The second part of the Segment Addition Postulate is the converse of the first part. Combine the statements to form a true biconditional statement. If B lies between points A and C, then AB + BC = AC. Converse: If AB + BC = AC; then B lies between points A and C. Combine these statements

Example 5: Writing a Postulate as a Biconditional Statement • Segment Addition Postulate – Point B lies between points A and C if and only if AB + BC = AC.

Biconditionals and Definitions LESSON 2 -2 Additional Examples Consider this true conditional statement. Write its converse. If the converse is also true, combine the statements as a biconditional. Conditional: If x = 5, then x + 15 = 20. To write the converse, exchange the hypothesis and conclusion. Converse: If x + 15 = 20, then x = 5. When you subtract 15 from each side to solve the equation, you get x = 5. Because both the conditional and its converse are true, you can combine them in a true biconditional using the phrase if and only if. Biconditional: x = 5 if and only if x + 15 = 20. Quick Check

Biconditionals and Definitions LESSON 2 -2 Additional Examples Write the two statements that form this biconditional. Biconditional: Lines are skew if and only if they are noncoplanar. A biconditional is written as two conditionals that are converses of each other. Conditional: If lines are skew, then they are noncoplanar. Converse: If lines are noncoplanar, then they are skew. Quick Check

Biconditionals and Definitions LESSON 2 -2 Additional Examples Show that this definition of triangle is reversible. Then write it as a true biconditional. Definition: A triangle is a polygon with exactly three sides. The original conditional is true. Conditional: If a polygon is a triangle, then it has exactly three sides. The converse is also true. Converse: If a polygon has exactly three sides, then it is a triangle. Because both statements are true, they can be combined to form a biconditional. A polygon is a triangle if and only if it has exactly three sides. Quick Check

Biconditionals and Definitions LESSON 2 -2 Additional Examples Is the following statement a good definition? Explain. An apple is a fruit that contains seeds. The statement is true as a description of an apple. Now exchange “An apple” and “a fruit that contains seeds, ” and the reverse reads: A fruit that contains seeds is an apple. There are many other fruits containing seeds that are not apples, such as lemons and peaches. These are counterexamples, so the reverse of the statement is false. The original statement is not a good definition because the statement is not reversible. Quick Check

Assignment • Pg. 78 24 -46, 55 -69