P HU ROF GO ES YA OR E

P HU ROF GO ES YA OR ÑE Z ISOMETRIA

ISOMETRIA • ISO = IGUAL • METRIA= MEDIDA EN UNA TRANSFORMACION ISOMETRICA • NO SE ALTERA LA FORMA NI EL TAMAÑO DE LA FIGURA. • SOLO SE CAMBIA DE POSICIÓN (ORIENTACION O SENTIDO DE ESTA)

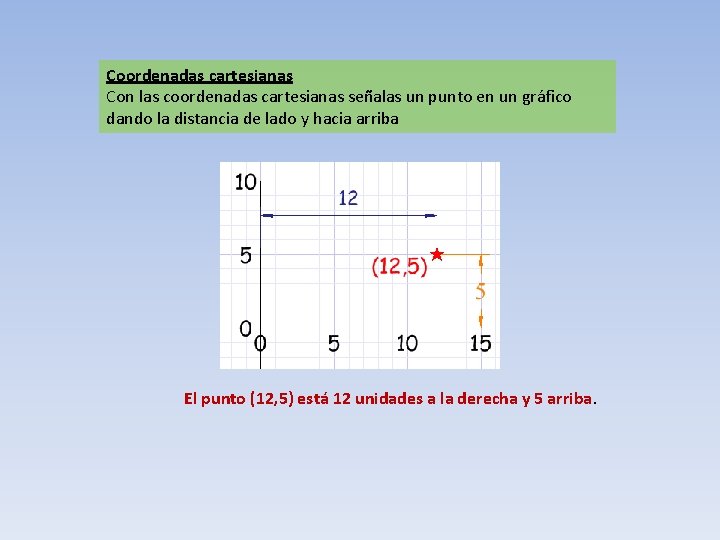
Coordenadas cartesianas Con las coordenadas cartesianas señalas un punto en un gráfico dando la distancia de lado y hacia arriba El punto (12, 5) está 12 unidades a la derecha y 5 arriba.

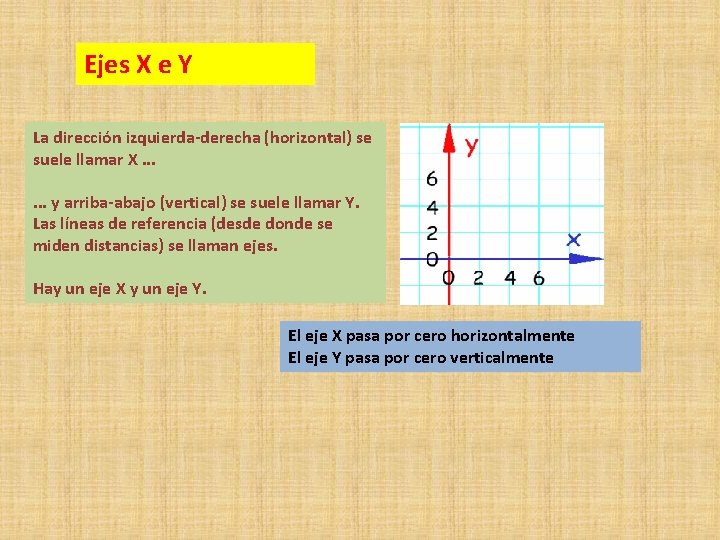
Ejes X e Y La dirección izquierda-derecha (horizontal) se suele llamar X. . . y arriba-abajo (vertical) se suele llamar Y. Las líneas de referencia (desde donde se miden distancias) se llaman ejes. Hay un eje X y un eje Y. El eje X pasa por cero horizontalmente El eje Y pasa por cero verticalmente

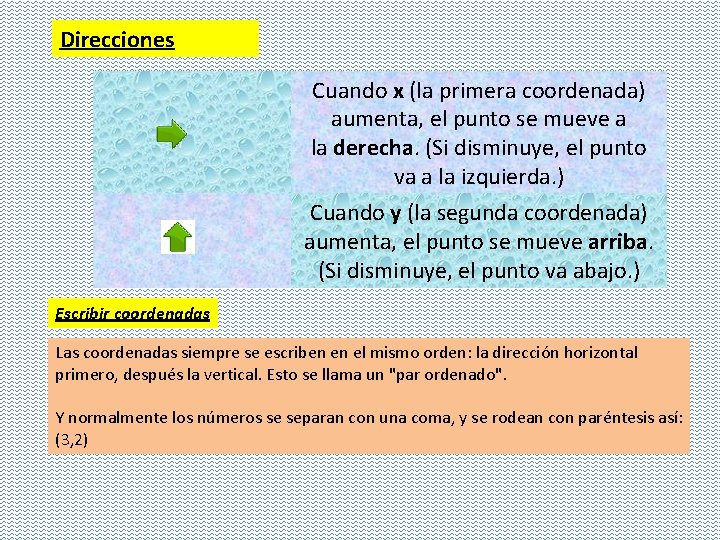
Direcciones Cuando x (la primera coordenada) aumenta, el punto se mueve a la derecha. (Si disminuye, el punto va a la izquierda. ) Cuando y (la segunda coordenada) aumenta, el punto se mueve arriba. (Si disminuye, el punto va abajo. ) Escribir coordenadas Las coordenadas siempre se escriben en el mismo orden: la dirección horizontal primero, después la vertical. Esto se llama un "par ordenado". Y normalmente los números se separan con una coma, y se rodean con paréntesis así: (3, 2)

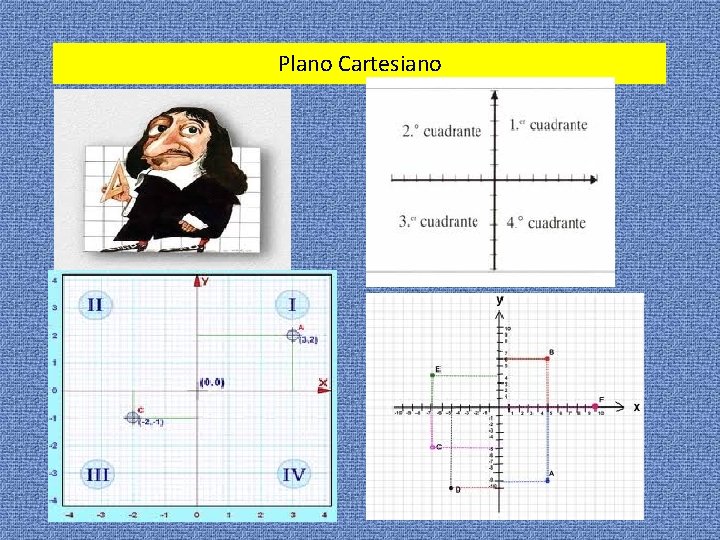
Plano Cartesiano

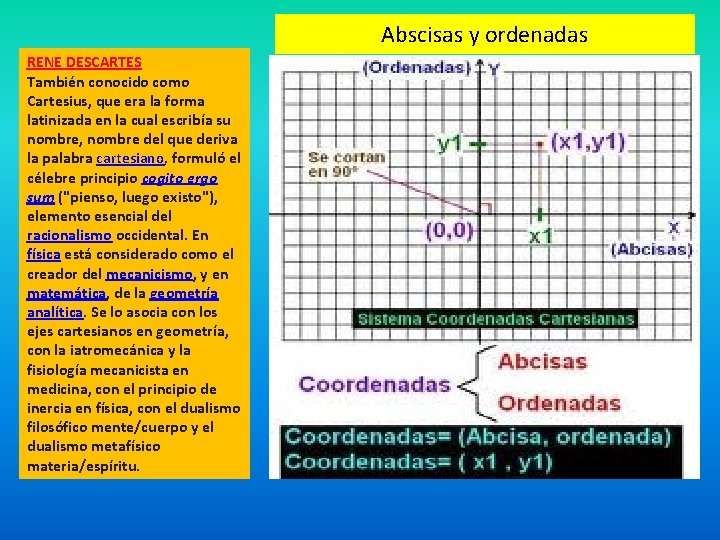
Abscisas y ordenadas RENE DESCARTES También conocido como Cartesius, que era la forma latinizada en la cual escribía su nombre, nombre del que deriva la palabra cartesiano, formuló el célebre principio cogito ergo sum ("pienso, luego existo"), elemento esencial del racionalismo occidental. En física está considerado como el creador del mecanicismo, y en matemática, de la geometría analítica. Se lo asocia con los ejes cartesianos en geometría, con la iatromecánica y la fisiología mecanicista en medicina, con el principio de inercia en física, con el dualismo filosófico mente/cuerpo y el dualismo metafísico materia/espíritu.

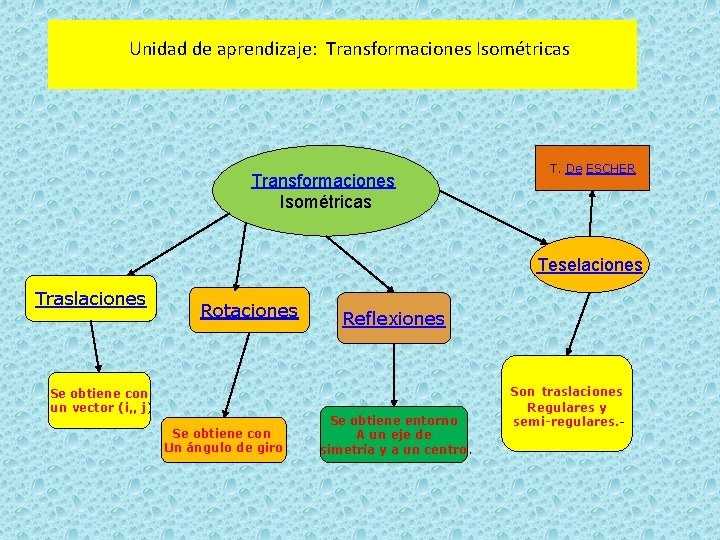
Unidad de aprendizaje: Transformaciones Isométricas T. De ESCHER Teselaciones Traslaciones Rotaciones Se obtiene con un vector (i, , j) Se obtiene con Un ángulo de giro Reflexiones Se obtiene entorno A un eje de simetría y a un centro. Son traslaciones Regulares y semi-regulares. -

Transformaciones Isométricas Las transformaciones isométricas son transformaciones de figuras en el plano que se realizan sin variar las dimensiones y el área de las mismas; la figura inicial y la final son semejantes, y geométricamente congruentes. La palabra isometría tiene su origen en el griego iso(igual o mismo) y metria (medir), una definición cercana es igual medida. Existen tres tipos de isometrías: traslación, simetría y rotación.

Transformaciones Isométricas Son figuras que cambian de posición, según un vector, un ángulo de rotación y entorno a un eje de simetría.

Es una Transformación Isométrica que produce un desplazamiento paralelo de una figura, de acuerdo a un vector, y por lo tanto, mantiene sus lados de igual medida y paralelos que los de la figura original. Se llama traslación definida por el vector v a la transformación geométrica que hace corresponder a caca punto A del plano el punto A’, de la forma que el vector AA’ sea equipolente a v.

Traslaciones Se puede considerar una traslación como el movimiento que se hace al deslizar una figura, en línea recta, manteniendo su forma y tamaño.

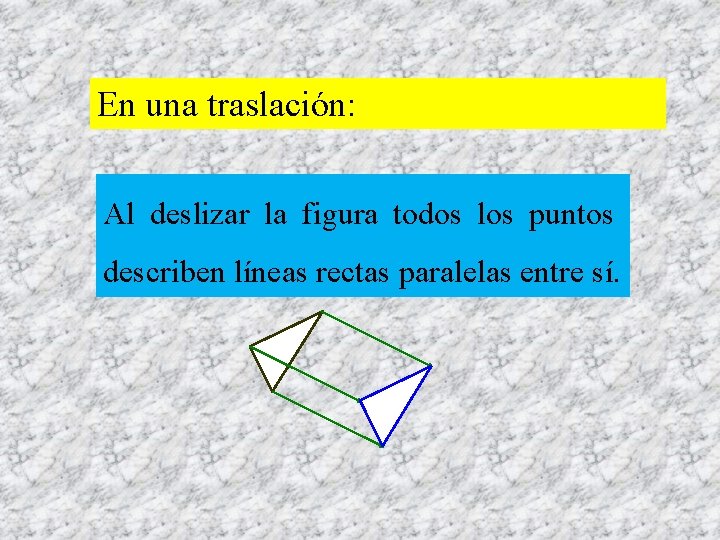
En una traslación: Al deslizar la figura todos los puntos describen líneas rectas paralelas entre sí.

En una traslación se distinguen tres elementos: Dirección (horizontal, vertical u oblicua). Sentido (derecha, izquierda, arriba, abajo). Magnitud del desplazamiento (distancia entre la posición inicial y final de cualquier punto)

Traslaciones en un sistema de ejes coordenados En este caso se debe señalar las coordenadas del vector de traslación. Estas son un par ordenado de números (x, y), donde x representa el desplazamiento horizontal e y representa el desplazamiento vertical.

En el par ordenado la primera componente recibe el nombre de abscisa y la segunda componente el nombre de ordenada.

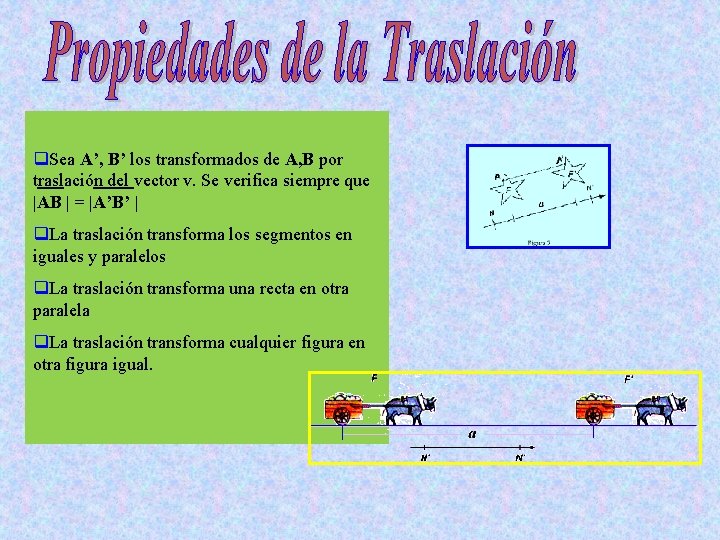
q. Sea A’, B’ los transformados de A, B por traslación del vector v. Se verifica siempre que |AB | = |A’B’ | q. La traslación transforma los segmentos en iguales y paralelos q. La traslación transforma una recta en otra paralela q. La traslación transforma cualquier figura en otra figura igual.

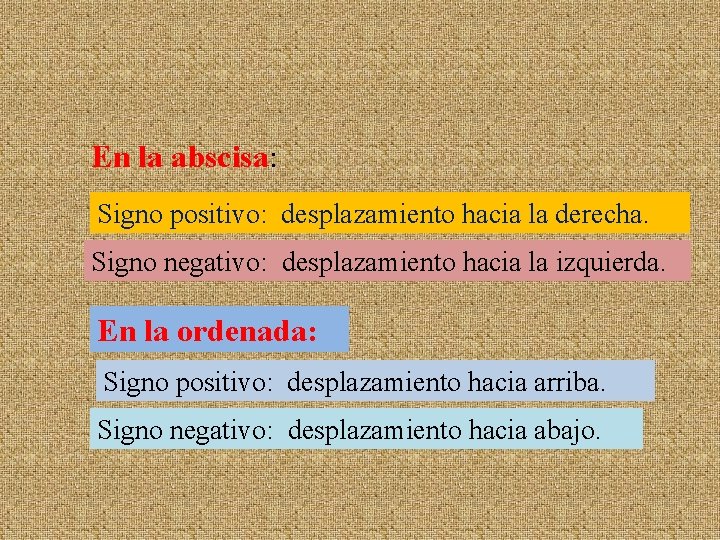
En la abscisa: Signo positivo: desplazamiento hacia la derecha. Signo negativo: desplazamiento hacia la izquierda. En la ordenada: Signo positivo: desplazamiento hacia arriba. Signo negativo: desplazamiento hacia abajo.

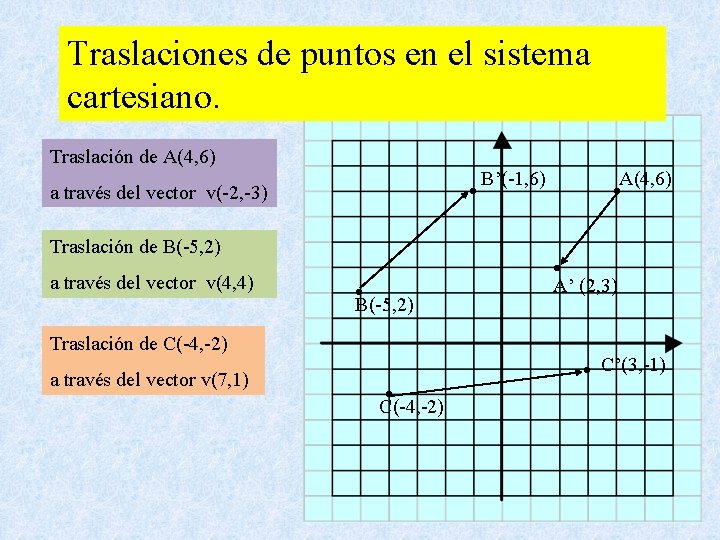
Traslaciones de puntos en el sistema cartesiano. Traslación de A(4, 6) a través del vector v(-2, -3) Traslación de B(-5, 2) a través del vector v(4, 4) A(4, 6) B(-5, 2) Traslación de C(-4, -2) a través del vector v(7, 1) B’(-1, 6) A’ (2, 3) C’(3, -1) C(-4, -2)

"Srta Rotación" Es una Transformación. Isométrica, tal que los puntos simétricos pertenecen a un mismo arco de circunferencia de centro el punto de rotación y ángulo de medida en el cual se efectuó la rotación. • http: //www. disfrutalasmatematicas. com/geometria/rotaciones. html El ángulo se dice positivo si se realiza en sentido contrario a los punteros del reloj, y negativo en el otro caso.

q. Los segmentos que unen los puntos homólogos son iguales. q. Una rotación transforma los puntos de un segmento en los de otro igual a él. q. Una rotación trasforma las rectas en otras rectas. q. Una rotación trasforma un ángulo en otro igual a él. De ellos se deduce que dos figuras homólogas bajo las transformaciones de una rotación son directamente iguales. q. El centro de giro O es homólogo de sí mismo y, por lo tanto, es punto doble.

En una rotación se identifican tres elementos: • El punto de rotación (centro de rotación), punto en torno al cual se efectúa la rotación . La magnitud de rotación, que corresponde al ángulo, éste está determinado por un punto cualquiera de la figura, el centro de rotación (vértice del ángulo) y el punto correspondiente de la figura obtenida después de la rotación. El sentido de giro, positivo (antihorario), negativo (horario) N M M’ . O N’

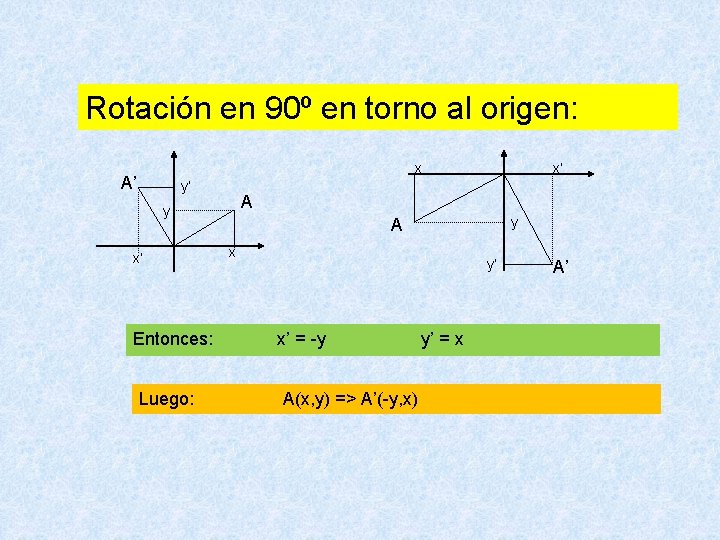
Rotación en 90º en torno al origen: x A’ y’ A y x’ Entonces: Luego: x’ y A x y’ x’ = -y A(x, y) => A’(-y, x) y’ = x A’

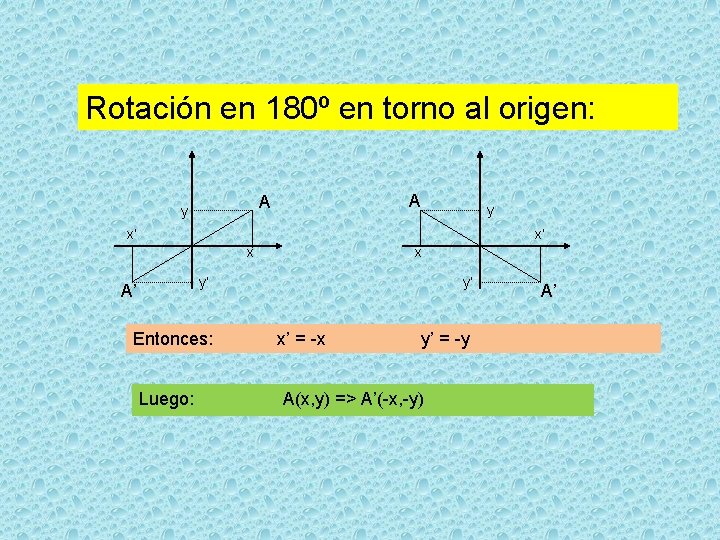
Rotación en 180º en torno al origen: A A y y x’ x’ x x y’ A’ Entonces: Luego: y’ x’ = -x y’ = -y A(x, y) => A’(-x, -y) A’

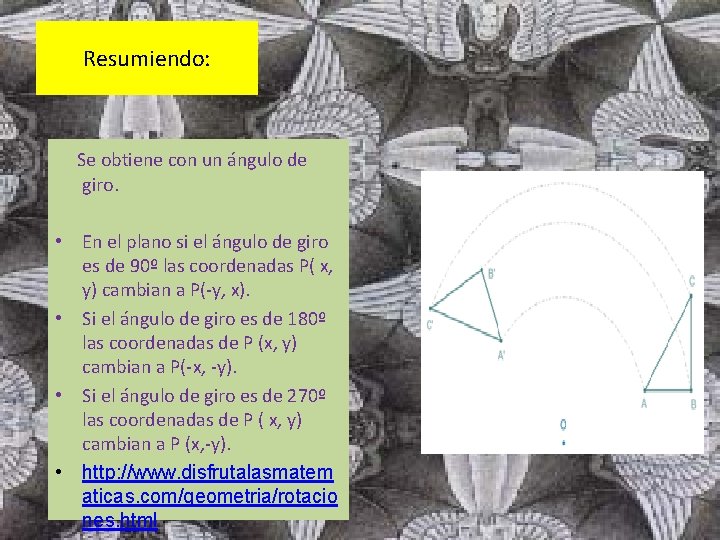
Resumiendo: Se obtiene con un ángulo de giro. • En el plano si el ángulo de giro es de 90º las coordenadas P( x, y) cambian a P(-y, x). • Si el ángulo de giro es de 180º las coordenadas de P (x, y) cambian a P(-x, -y). • Si el ángulo de giro es de 270º las coordenadas de P ( x, y) cambian a P (x, -y). • http: //www. disfrutalasmatem aticas. com/geometria/rotacio nes. html

Simetrías o reflexiones Se puede considerar una simetría como aquel movimiento que aplicado a una figura geométrica, produce el efecto de un espejo.

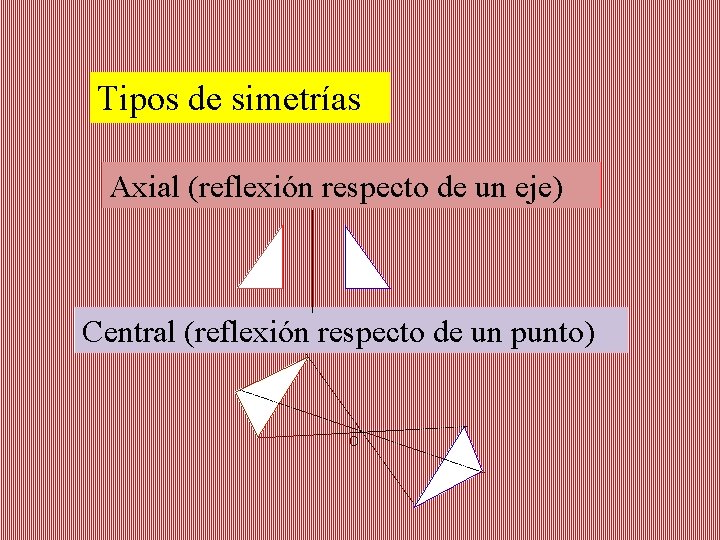
Tipos de simetrías Axial (reflexión respecto de un eje) Central (reflexión respecto de un punto) O

Es una Transformación Isométrica respecto a un eje de simetría de modo que el segmento que une dos puntos simétricos es perpendicular al eje de simetría, siendo éste la mediatriz de dicho segmento. O La recta OX se llama eje de simetría X

q. Todo punto del plano tiene uno y sólo un homólogo bajo una simetría axial. q. Todos los puntos del eje de simetría son homólogos de sí mismos; se dice que son puntos dobles. q. La simetría axial es una isometría, es decir, mantiene las distancias. q. Las simetrías axiales transforman los segmentos en segmentos iguales y las rectas en otras rectas que cortan a las primeras en puntos M del eje de simetría.

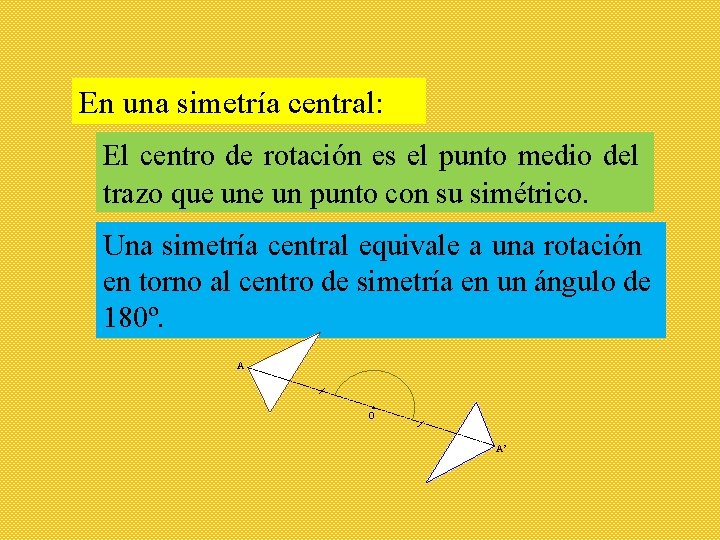
En una simetría central: El centro de rotación es el punto medio del trazo que un punto con su simétrico. Una simetría central equivale a una rotación en torno al centro de simetría en un ángulo de 180º. A O A’

Se llama simetría central a una transformación geométrica que hace corresponder a cada punto A del plano otro punto A’ del plano tales que están alineados con un punto fijo O, a distinto lado de él y a la misma distancia O El punto O recibe el nombre de Centro de simetría.

q. En una simetría de centro O, A’ es el homólogo de A y recíprocamente; por lo tanto, los elementos homólogos en una simetría central se corresponden doblemente. RESUMIENDO