Outline Magnetic dipole moment Dipoles and monopoles Magnetization

Outline � Magnetic � dipole moment Dipoles and monopoles � Magnetization � Magnetic susceptibility and permeability � Magnetic induction � Poisson’s equation and potential for magnetic field � Potential fields in practice: Vertical component of gravity � Each of the vertical components of magnetic field � � Total field

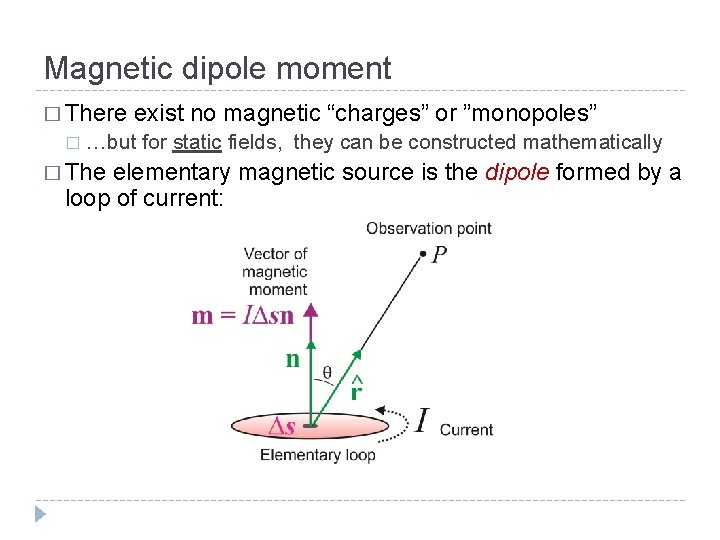
Magnetic dipole moment � There � exist no magnetic “charges” or ”monopoles” …but for static fields, they can be constructed mathematically � The elementary magnetic source is the dipole formed by a loop of current:

Magnetic Potential a shift Dr of the observation point � If curl (B) = 0 (no current at the observation point), field B can be presented as a gradient of a potential V: � Consider or: � Biot-Savart law: Cm depends on the unit system: emu: Dimensionless Cm = 1 SI: Cm = m 0/4 p = 10 -7 H/m “Henry”, unit of inductance is a unit vector along r

Magnetic Potential � Therefore, the change in the potential: The first equation here uses: The second equation assumes an infinitesimal loop uses The contour integral gives twice the area of the loop: � Hence the change in V over distance Dr: � and

Magnetic Potential � Therefore, that the potential the magnetic potential equals: Note decreases along The const is usually taken zero, so that the direction of m, and hence B is generally oriented along m � Note two properties different from the monopole potential for gravity: 1. 2. The potential decays with distance as 1/r 2 It also depends on the direction (zero within the plane orthogonal to m and opposite signs in the directions parallel and opposite to m)

Poisson’s relation � The dipole field (V 1/r 2) equals a derivative of a “monopole field” (V 1/r) with respect to the positions of the source (r 0) or observation point (r) : This is simply the spatial derivative in the direction of the magnetic moment, m � Therefore, the magnetic field of a structure with given direction of magnetization n is related to its gravity field (Poisson’s relation):

Magnetic Monopoles � The dipole field can be presented as produced by two monopoles separated by an arbitrary (small) distance a: where and is the pole strength

Magnetic filed of a uniform magnetization � The magnetic potential of a single magnetic moment m: � Consider m uniformly distributed in space with density M: � Then, similarly to Gauss’s theorem in gravity, integration of 1/r 2 over all sources in the volume gives the potential uniformly decreasing in the direction of M: and therefore magnetic field:

Magnetic Induction � Magnetic moments within the medium (remanent or induced) cause magnetic field (take SI units now, Cm = m 0/4 p): field adds to the filed B = m 0 H produced by external currents. The sum is called the magnetic induction field (this field acts on our magnetometer): � This � If the magnetization is induced: then: m = m 0(1+k) is called magnetic permeability k is called magnetic susceptibility

Components as potential fields � If f(x) is a potential field (satisfies the Laplace equation, ), then its gradient evaluated in a fixed direction is also a potential field: � This means that: � � � Vertical component of gravity satisfies Laplace equation Each of the three components of magnetic field satisfies Laplace equation However, when measured on the near-spherical Earth, the “vertical” components are actually radial derivatives � � These do not rigorously satisfy the Laplace equation The error is small (as the ratio of the survey size to the radius of curvature)

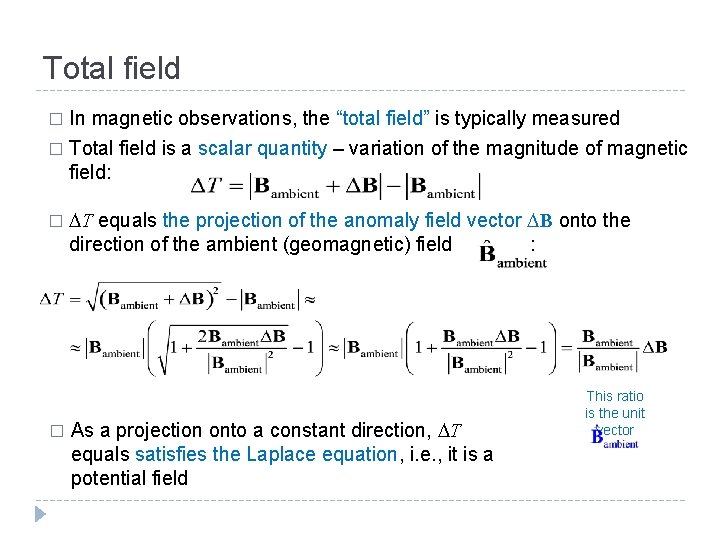
Total field In magnetic observations, the “total field” is typically measured � Total field is a scalar quantity – variation of the magnitude of magnetic field: � � � DT equals the projection of the anomaly field vector DB onto the direction of the ambient (geomagnetic) field : As a projection onto a constant direction, DT equals satisfies the Laplace equation, i. e. , it is a potential field This ratio is the unit vector