NRA Top k query processing using Non Random

NRA Top k query processing using Non Random Access Only sequential access Algorithm 1) 2) 3) 4) 5) 6) 7) 8) scan index lists in parallel; consider dj at position posi in Li; E(dj) : = E(dj) Є {i}; highi : = si(q, dj); bestscore(dj) : = aggr{x 1, . . . , xm) § with xi : = si(q, dj) for i Є E(dj), highi for i Є E(dj); worstscore(dj) : = aggr{x 1, . . . , xm) § with xi : = si(q, dj) for i Є E(dj), 0 for i Є E(dj); top-k : = k docs with largest worstscore; threshold : = bestscore{d | d not in top-k}; if min worstscore top-k ≥ threshold then exit;

NRA 0. 6+0. 9=2. 1 List 2 List 3 worst score Candidates item 25 item 17 item 83 0. 6 0. 9 item 83 [0. 9, 2. 1] item 78 item 38 item 17 0. 5 0. 6 0. 7 item 17 [0. 6, 2. 1] item 83 item 14 item 61 0. 4 0. 6 0. 3 item 25 [0. 6, 2. 1] item 17 0. 3 item 5 0. 6 item 81 0. 2 item 21 item 83 item 65 0. 2 0. 5 0. 1 item 91 item 21 item 10 0. 1 0. 3 0. 1 item 44 0. 1 best-score Min top-2 score : 0. 6 Threshold (Max of unseen tuples): 2. 1 Pruning Candidates: Min top-2 < best score of candidate Stopping Condition Threshold < min top-2 ?

NRA List 1 List 2 List 3 worst score Candidates item 25 item 17 item 83 0. 6 0. 9 item 17 [1. 3, 1. 8] item 78 item 38 item 17 0. 5 0. 6 0. 7 item 83 [0. 9, 2. 0] item 83 item 14 item 61 0. 4 0. 6 0. 3 item 25 [0. 6, 1. 9] item 17 0. 3 item 81 0. 2 item 38 [0. 6, 1. 8] item 21 item 83 item 65 0. 2 0. 5 0. 1 item 78 [0. 5, 1. 8] item 5 0. 6 item 91 item 21 item 10 0. 1 0. 3 0. 1 item 44 0. 1 best-score Min top-2 score : 0. 9 Threshold (Max of unseen tuples): 1. 8 Pruning Candidates: Min top-2 < best score of candidate Stopping Condition Threshold < min top-2 ?

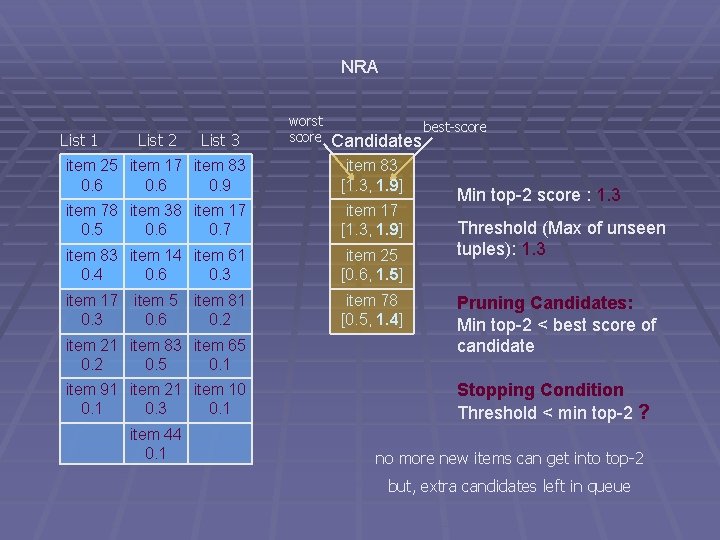
NRA List 1 List 2 List 3 worst score Candidates item 25 item 17 item 83 0. 6 0. 9 item 83 [1. 3, 1. 9] item 78 item 38 item 17 0. 5 0. 6 0. 7 item 17 [1. 3, 1. 9] item 83 item 14 item 61 0. 4 0. 6 0. 3 item 25 [0. 6, 1. 5] item 17 0. 3 item 78 [0. 5, 1. 4] item 5 0. 6 item 81 0. 2 item 21 item 83 item 65 0. 2 0. 5 0. 1 item 91 item 21 item 10 0. 1 0. 3 0. 1 item 44 0. 1 best-score Min top-2 score : 1. 3 Threshold (Max of unseen tuples): 1. 3 Pruning Candidates: Min top-2 < best score of candidate Stopping Condition Threshold < min top-2 ? no more new items can get into top-2 but, extra candidates left in queue

NRA List 1 List 2 List 3 worst score Candidates item 25 item 17 item 83 0. 6 0. 9 item 17 1. 6 item 78 item 38 item 17 0. 5 0. 6 0. 7 item 83 [1. 3, 1. 9] item 83 item 14 item 61 0. 4 0. 6 0. 3 item 25 [0. 6, 1. 4] item 17 0. 3 item 5 0. 6 item 81 0. 2 item 21 item 83 item 65 0. 2 0. 5 0. 1 item 91 item 21 item 10 0. 1 0. 3 0. 1 item 44 0. 1 best-score Min top-2 score : 1. 3 Threshold (Max of unseen tuples): 1. 1 Pruning Candidates: Min top-2 < best score of candidate Stopping Condition Threshold < min top-2 ? no more new items can get into top-2 but, extra candidates left in queue

NRA List 1 List 2 List 3 Candidates item 25 item 17 item 83 0. 6 0. 9 item 83 1. 8 item 78 item 38 item 17 0. 5 0. 6 0. 7 item 17 1. 6 item 83 item 14 item 61 0. 4 0. 6 0. 3 item 17 0. 3 item 5 0. 6 item 81 0. 2 item 21 item 83 item 65 0. 2 0. 5 0. 1 item 91 item 21 item 10 0. 1 0. 3 0. 1 item 44 0. 1 Min top-2 score : 1. 6 Threshold (Max of unseen tuples): 0. 8 Pruning Candidates: Min top-2 < best score of candidate

NRA § NRA performs only sorted accesses (SA) (No Random Access) § Random access (RA) § § § lookup actual (final) score of an item costlier than SA (100 – 100, 000 times), c. R/c. S : = (cost of RA)/(cost of SA) often very useful § CA (Combined Algorithm), (Fagin et al. , 2001) § one RA after every c. R/c. S SAs § total cost of SA ~ total cost of RA § Measure of effectiveness (access cost): #SA + c. R/c. S x #RA § Full-merge: compute scores for all items followed by partial sort § simple and efficient § important baseline for any top-k algorithm § Problems with NRA, CA § high bookkeeping overhead § for “high” values of k, gain in even access cost not significant

References § IO-Top-k: Index-access Optimized Top-k Query Processing Debapriyo Majumdar Max-Planck-Institut für Informatik Saarbrücken, Germany Joint work with Holger Bast, Ralf Schenkel, Martin Theobald, Gerhard Weikum § Top-k Query Evaluation with Probabilistic Guarantees Martin Theobald, Gerhard Weikum, Ralf Schenkel