Newton and Kepler Newtons Law of Gravitation The

Newton and Kepler

Newton’s Law of Gravitation

The Law of Gravity Isaac Newton deduced that two particles of masses m 1 and m 2, separated by a distance r, will attract each other with a force This is the universal law of gravity. If two spheres were treated as if all the mass were concentrated at the center of the sphere, the same law applies. The universal gravity constant G is. The force of gravity on a person of mass m due to the earth’s mass ME is called the person’s weight. Thus so At the earth’s surface, r ' RE and g = 9. 80 m/s 2.

Gravitational Potential Energy Gravity is a conservative force, and we may define a potential energy associated with it. The gain in potential energy is the work you must do to lift a mass from one point to another. Work is done against gravity only when the displacement is up or down. Going sideways to r doesn’t require any work. The work done is the gain in potential energy U(r) For objects a small distance h above the surface of the earth where h << RE. , we set r 1 = RE and r 2 = RE + h and the equation becomes We neglected h. R << R 2. . If we choose U = 0 at r = RE, then U = mgh

Tides The tidal force arises because of the gravitational force between the two bodies acts on an axis connecting the two centers of gravity. The earth is subject to the moon's gravitational forces causing the water in the oceans to change their shape, forming bulges on the sides near the moon and far from the moon. The bulges lie on the axis connecting the two centers of gravity of the bodies.

When the Moon and Sun are in a line with Earth, the tides are higher. We call those spring tides. When they're at right angles in outer space, the tides are lower. We call those neap tides. The moon, which is approximately 386, 240 km from the earth, exerts a greater influence on the tides then does the sun, which sits 150 million km from the earth. Although the mass of the moon is only about a hundred millionths of the sun's mass, it still exerts a greater force on the ocean the sun does because it is about 400 times closer to the earth than the sun is. The sun's tidal influence is thus about half (46 percent) of the moon's.

Problems 1. ) Determine the minimum speed that a rocket at the surface of the earth must have to escape completely the earth’s gravity field. Solution The rockets energy is conserved. We want the rocket to go far away (r = 1), and barely reach there (v = 0). Thus U 1 + KE 1 = 0 + 0. so vesc is the escape velocity. If the values for RE = 6371 km and ME = 5. 9736 £ 1024 kg are inserted in the equation, then the escape velocity from the earth is 11. 2 km/s. For the values of Rsun=6. 955 £ 105 km and Msun= 1. 99 £ 1030 kg, the escape velocity from the solar system is 618 km/s.

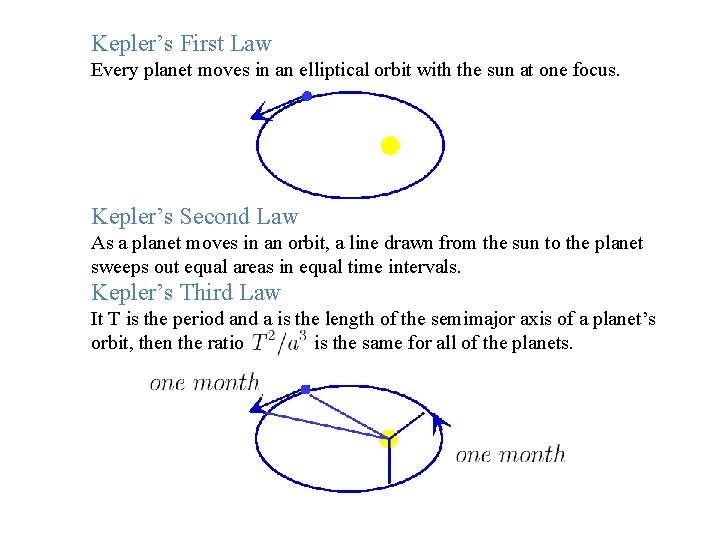
Kepler’s First Law Every planet moves in an elliptical orbit with the sun at one focus. Kepler’s Second Law As a planet moves in an orbit, a line drawn from the sun to the planet sweeps out equal areas in equal time intervals. Kepler’s Third Law It T is the period and a is the length of the semimajor axis of a planet’s orbit, then the ratio is the same for all of the planets.

Kepler’s Second Law is derived by using the conservation of angular momentrum. because the lever arm is 0 and v is parallel to v, the equation equals zero. Thus the angular momentum is a constant and is conserved. In time dt the planet has displacement out an area d. A. But the magnitude of the area of the parallelogram formed by half of this so and sweeps is , and. d. A is just

or Kepler’s third law is easy to prove using the force of gravity. The gravitational force is equal and opposite to the centripetal force needed to move the planet in a circle. Thus The orbital speed is v = 2¼ r/T where T is the period of the motion. or

Problems 1. ) Geosynchronous satellites are placed in an orbit in the equatorial plane such that they are always above a given point on the earth’s surface, that is, their period is 24 hours. How far from the center of earth is such a satellite? Solution From the derivation of Kepler’s third law we have the equation Substituting T = (24 h)(3600 s/h) and ME = 5. 9736 £ 1024 kg and solving for r results in r = 42, 300 km. 2. ) The moon goes around the earth every 27. 3 days. The mass of the earth is 5. 98 £ 1024 kg. Determine the earth to moon distance

Solution Solve for r. r = 3. 83 £ 108 m. 3. ) An artificial satellite of mass m travels at a constant speed in a circular orbit of radius R around the earth (mass ME). What is the speed of the satellite? Solution The centripetal force on the satellite is provided by Earth’s gravitational pull. Therefore Solving this equation for v yields

Note that the satellite’s speed doesn’t depend on its mass, even if it were a baseball, if its orbit radius were R, then it would still be.