Intercept Problems Intercept Problems AGENDA Intercept Problem Objectives

Intercept Problems

Intercept Problems • AGENDA: – Intercept Problem Objectives – Intercept Example (simple) – Intercept Example (two-leg maneuver) • Applicable reading: MBW Ch 13.

Intercept Problems (Objectives) An intercept problem is similar to a stationing problem. The objectives of this problem are: 1. To determine the other contact’s course and speed. 2. To determine course and maneuver time required to intercept a contact using a given intercept speed. 3. To determine the course and speed to required to intercept the contact at a given time. 4. Constant bearing, decreasing range problem: To determine minimal acceptable CPA. Concepts learned in previous lessons should be applied.

Intercept Problem (Example) e. g: You are the OOD onboard USS HUÉ CITY, steering 045ºT, speed 15 kts. At 0200 your radar picks up a contact bearing 308ºT at 24, 500 yds. The course and speed of the contact is determined by CIC to be 150ºT, 15 kts. The CO orders you to intercept the contact using a speed of 21 kts. Find the course and required time of intercept.

Intercept Problem (Example) 1. In order that students may understand better it is suggested that the contact be placed in the center as the reference ship, and draw the “er” vector to represent course (150ºT) and speed (15 kts) of the contact. 2. Plot M 1 (reciprocal of 308ºT - 180ºT = 128ºT). 3. Since you are the maneuvering ship, set a collision course for the contact drawing a line from M 1 to the center of the moboard for M 2. The direction of this line determines the DRM (308ºT and MRM that will be the distance between M 1 and M 2 (24, 500 yds).

Intercept Problem (Example) 4. Draw a line from the head of the “er” vector parallel to the DRM. Having measured the stationing speed (21 kts) on the dividers from the center of the moboard (e) and the other end will intersect the “rm” line. This is point “m”. The length of the “rm” vector is the SRM (34 kts). 5. The “em” vector represents the course and speed to intercept the contact. Course is 292 T. 6. The time required for the intercept can be determined by using the MRM (24, 500 yds) and the SRM (34 kts) on the nomogram (22 kts).
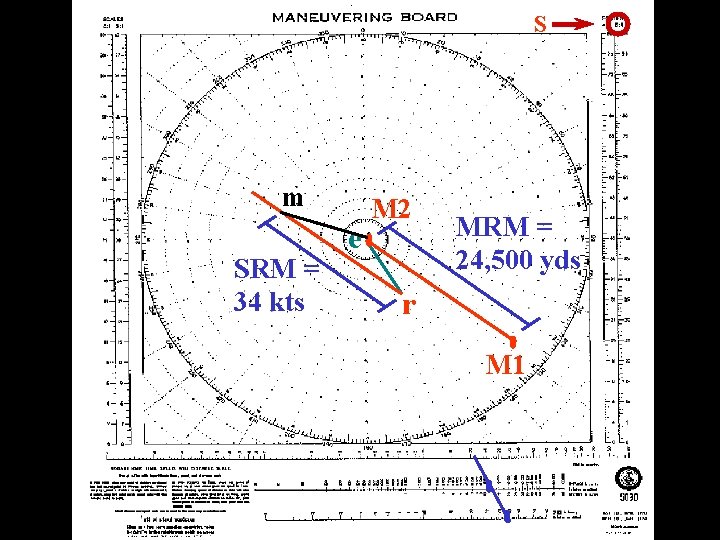
S m SRM = 34 kts e M 2 MRM = 24, 500 yds r M 1

Intercept Problem (Dog-leg example) eg: The guide is on course 000ºT, speed 15 kts. Currently you are in station bearing 270ºT, range 6, 000 yds from the guide. You are ordered to a new station bearing 090ºT, range 6, 000 yds from the guide. Use 27 kts and pass astern NO closer than 3, 000 yds from the guide to complete the maneuver. Find the two courses & total time required to complete the maneuver.

Intercept Problem (Dog-leg example) 1. In order that students may understand better it is suggested that the guide be placed in the center as the reference ship, and draw the “er” vector to represent course (000ºT) and speed (15 kts) of the guide. 2. Plot M 1 and draw a line from M 1 in the direction that will pass astern of the guide and tangent to the 3, 000 yard ring, and extend it indefinitely. This line will be your first DRM (120ºT). 3. Draw a second line from M 2 back towards the first DRM line so that I is tangent to the 3, 000 yd ring. This will be your second DRM (060ºT).

Intercept Problem (Dog-leg example) 4. Draw a line from the end of the “er” vector parallel to the first DRM. Having measured the stationing speed (27 kts) on the dividers from the center of the moboard and the other end will intersect the “rm” line. This is point “m”. The “rm” vector is the SRM (31 kts). The “em” vector represents the course and speed required for the first leg of the maneuver (092ºT). 5. Measure the distance from M 1 to the point where the first and second DRM lines cross. This will be your first MRM (7, 000 yds).

Intercept Problem (Dog-leg example) 6. The time required for the first leg of the maneuver can be determined by using the MRM (7, 000 yds) and the SRM (31 kts) on the nomogram (6 min 30 sec).
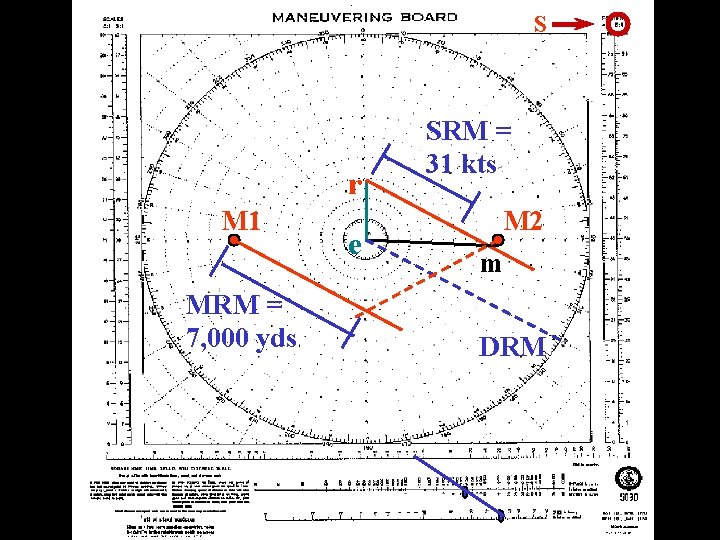
S r M 1 MRM = 7, 000 yds e SRM = 31 kts M 2 m DRM

Intercept Problem (Dog-leg example) 7. For the second leg, draw a line from the end of the “er” vector parallel to the second DRM. Having measured the stationing speed (27 kts) on the dividers from the center of the moboard and the other end will intersect the “rm” line. This is point “m 2”. The “rm” vector is the SRM (16 kts). 8. The “em” vector represents the course and speed required for the second leg of the maneuver (032 T). 9. Measure the distance from M 2 to the point where the first and second DRM lines cross. This will be your second MRM (7, 000 yds).

Intercept Problem (Dog-leg example) 10. The time required for the second leg of the maneuver can be determined by using the MRM (7, 000 yds) and the SRM (16 kts) on the nomogram (13 min). 11. To find total time, add the time required for each leg (6 min 30 sec + 13 min = 19 min 30 sec).
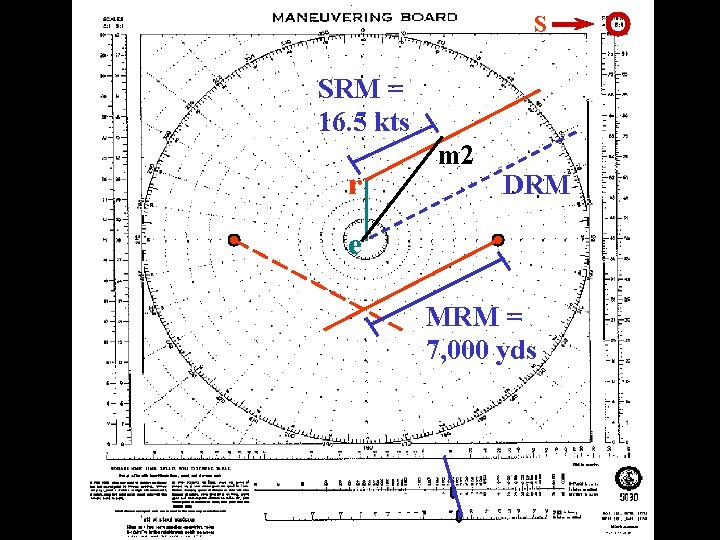
S SRM = 16. 5 kts r m 2 DRM e MRM = 7, 000 yds
- Slides: 15