h c r a e S Grovers Jake

h c r a e S Grovers Jake Biamonte Should be “one in four search” Jacob D. Biamonte biamonte@ieee. org Portland Quantum Logic Group

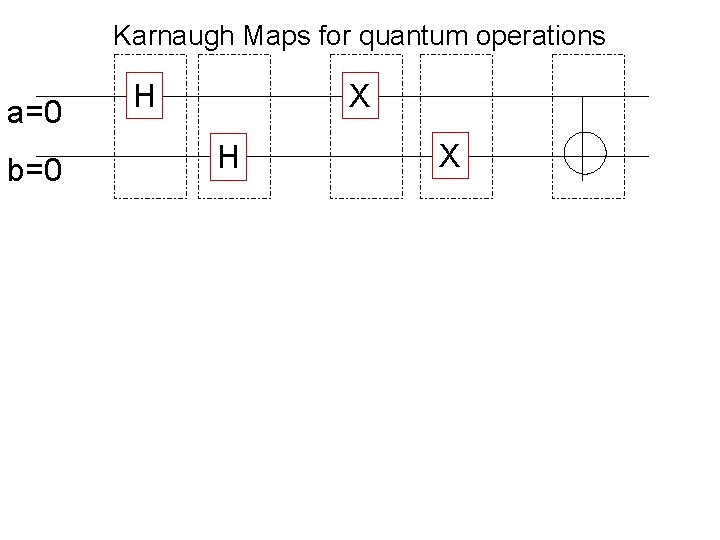
Karnaugh Maps for quantum operations a=0 b=0 H X

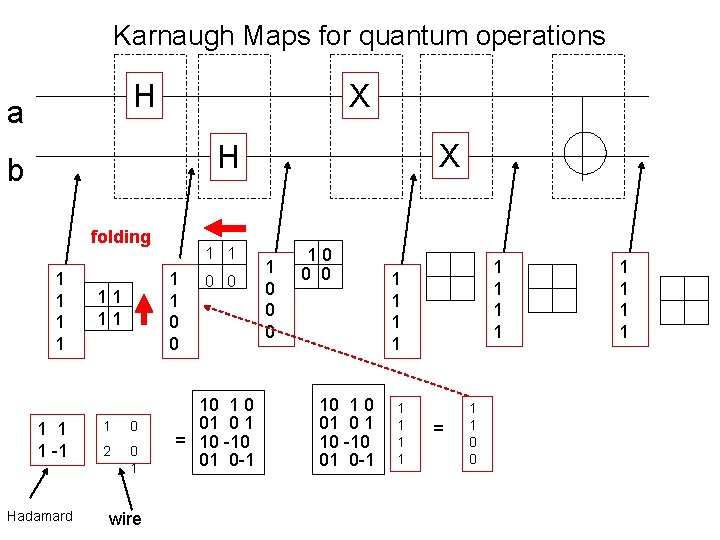
Karnaugh Maps for quantum operations H a X X H b folding 1 1 1 1 -1 Hadamard 1 1 0 0 11 11 1 0 2 0 1 wire 0 0 10 1 0 01 0 1 = 10 -10 01 0 -1 1 0 0 0 10 1 0 01 0 1 10 -10 01 0 -1 1 1 1 = 1 1 0 0 1 1

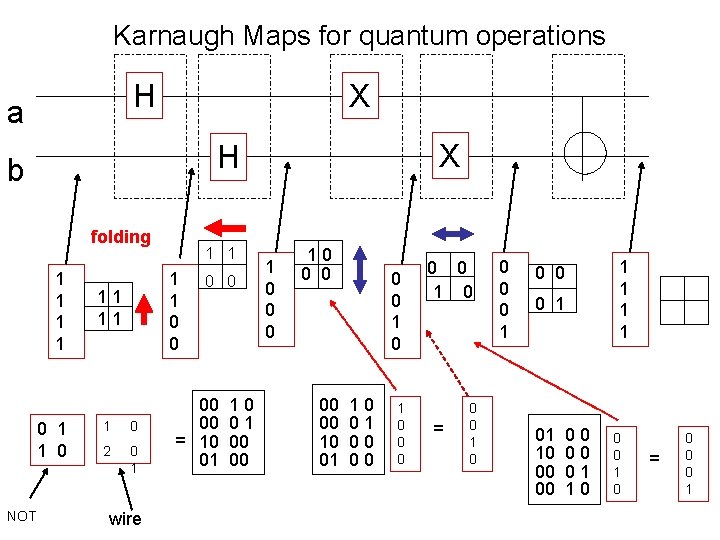
Karnaugh Maps for quantum operations H a X b folding 1 1 0 NOT X H 1 1 0 0 11 11 1 0 2 0 1 wire 0 0 00 00 = 10 01 00 00 1 0 0 0 10 0 0 00 00 10 01 00 00 1 0 0 0 1 0 = 0 0 1 1 1 0 0 0 1 01 10 00 00 01 10 0 0 1 0 = 0 0 0 1

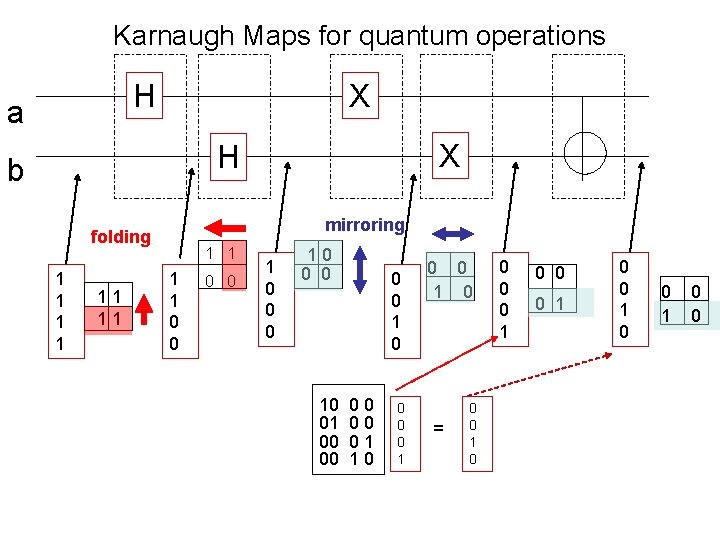
Karnaugh Maps for quantum operations H a X X H b mirroring folding 1 1 11 11 1 1 0 0 0 10 01 00 00 0 0 1 0 00 00 01 10 0 1 0 = 0 0 1 0 0 1 0 0

Why is this important? • This presentation shows clearly how to perform a so called 1 in 4 search • We start out with the basics 1 in 4 search

Pick your needle and I will find you a haystack The point of this slide is to show examples of 4 different oracles. Grovers search can tell between these oracles in a single iteration, classically we would need 3 iterations.

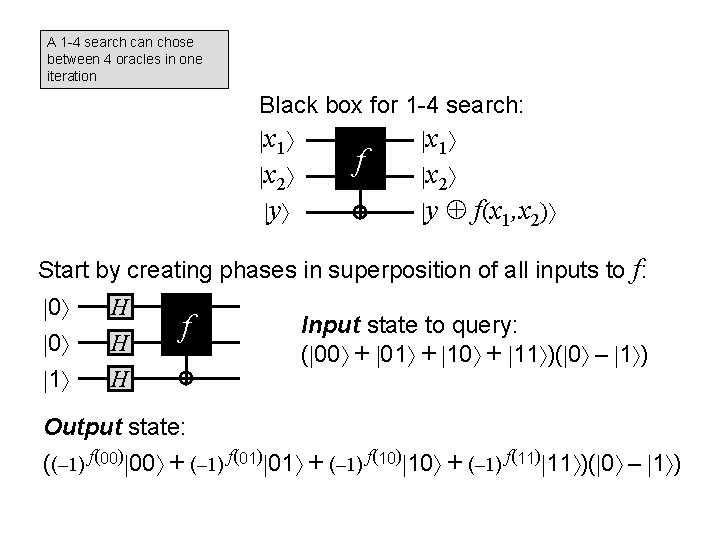
Properties of the oracle Let f : {0, 1}2 {0, 1} have the property that there is exactly one x {0, 1}2 for which f (x) = 1 Goal: find x {0, 1}2 for which f (x) = 1 Classically: 3 queries are necessary Quantumly: ? Only after 3 tests can we determine with certainty that the oracles is 1 for only a single input value x

A 1 -4 search can chose between 4 oracles in one iteration Black box for 1 -4 search: x 1 x 2 y f(x 1, x 2) Start by creating phases in superposition of all inputs to f: 0 0 1 H H H f Input state to query: ( 00 + 01 + 10 + 11 )( 0 – 1 ) Output state: ((– 1) f(00) 00 + (– 1) f(01) 01 + (– 1) f(10) 10 + (– 1) f(11) 11 )( 0 – 1 )

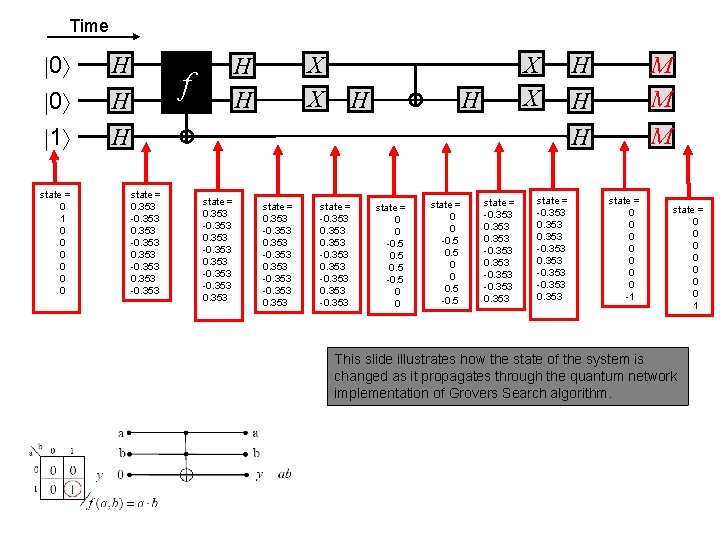
Time 0 0 1 state = 0 1 0 0 0 H H X X H H f H X X H H state = 0. 353 -0. 353 0. 353 state = -0. 353 -0. 353 state = 0 0 -0. 5 -0. 5 0 0 state = 0 0 -0. 5 0 0 0. 5 -0. 5 state = -0. 353 0. 353 -0. 353 H H M M H M state = 0 0 0 0 -1 state = 0 0 0 0 1 This slide illustrates how the state of the system is changed as it propagates through the quantum network implementation of Grovers Search algorithm.

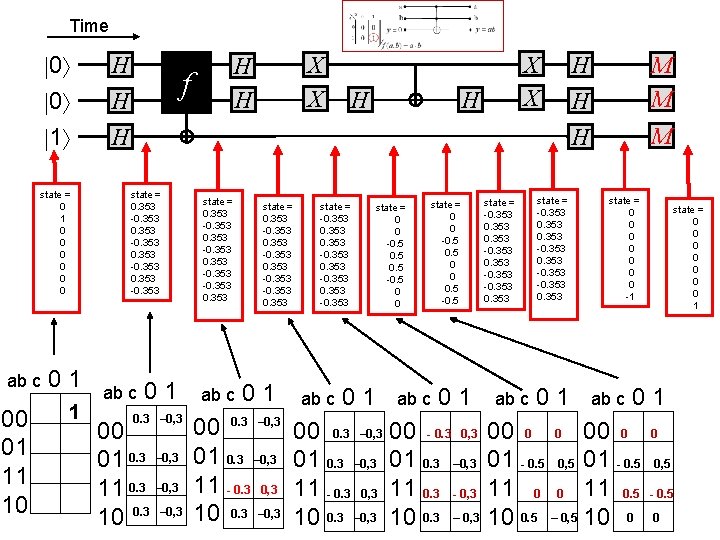
Time 0 0 1 state = 0 1 0 0 0 ab c 00 01 11 10 01 1 H H X X H H f H X X H H state = 0. 353 -0. 353 ab c 01 0. 3 – 0, 3 00 01 0. 3 – 0, 3 10 0. 3 – 0, 3 state = 0. 353 -0. 353 ab c state = 0. 353 -0. 353 01 00 0. 3 – 0, 3 01 0. 3 – 0, 3 11 - 0. 3 0, 3 10 0. 3 – 0, 3 state = -0. 353 -0. 353 ab c 01 state = 0 0 -0. 5 -0. 5 0 0 state = 0 0 -0. 5 0 0 0. 5 -0. 5 ab c 01 00 0. 3 – 0, 3 00 - 0. 3 0, 3 01 0. 3 – 0, 3 11 - 0. 3 0, 3 11 0. 3 - 0, 3 10 0. 3 – 0, 3 state = -0. 353 -0. 353 ab c state = -0. 353 -0. 353 01 H H M M H M state = 0 0 0 0 -1 ab c state = 0 0 0 0 1 01 00 0 01 - 0. 5 0, 5 01 - 0. 5 11 0 0 11 0. 5 10 0. 5 – 0, 5 10 0 0 0, 5 - 0. 5 0

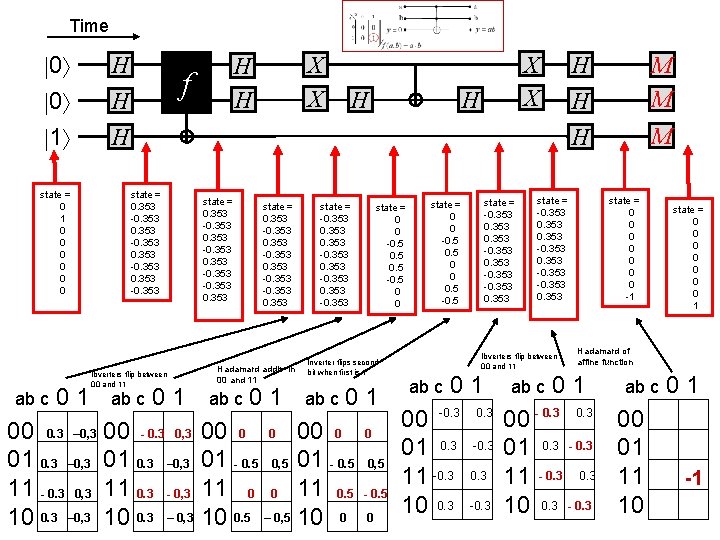
Time 0 0 1 state = 0 1 0 0 0 ab c 01 H H X X H H f H X X H H state = 0. 353 -0. 353 Ibverters flip between 00 and 11 ab c 01 00 0. 3 – 0, 3 00 - 0. 3 0, 3 01 0. 3 – 0, 3 11 - 0. 3 0, 3 11 0. 3 - 0, 3 10 0. 3 – 0, 3 state = 0. 353 -0. 353 0. 353 Hadamard addis in 00 and 11 ab c 01 state = -0. 353 -0. 353 state = 0 0 -0. 5 -0. 5 0 0 Inverter flips second bit when first is 1 ab c 01 00 0 01 - 0. 5 0, 5 01 - 0. 5 11 0 0 11 0. 5 10 0. 5 – 0, 5 10 0 0 0, 5 - 0. 5 0 state = -0. 353 -0. 353 state = 0 0 -0. 5 0 0 0. 5 -0. 5 01 00 -0. 3 01 0. 3 11 -0. 3 10 0. 3 -0. 3 M M H M state = 0 0 0 0 -1 state = -0. 353 -0. 353 Ibverters flip between 00 and 11 ab c H H ab c state = 0 0 0 0 1 Hadamard of affine function 01 00 - 0. 3 01 0. 3 - 0. 3 11 - 0. 3 10 0. 3 - 0. 3 ab c 00 01 11 10 01 -1

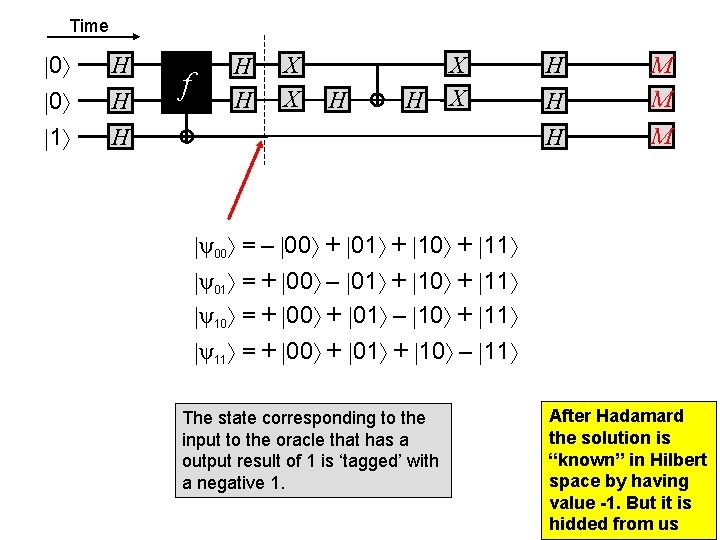
Time 0 0 1 H H f H H X X H H H M M H M ψ00 = – 00 + 01 + 10 + 11 ψ01 = + 00 – 01 + 10 + 11 ψ10 = + 00 + 01 – 10 + 11 ψ11 = + 00 + 01 + 10 – 11 The state corresponding to the input to the oracle that has a output result of 1 is ‘tagged’ with a negative 1. After Hadamard the solution is “known” in Hilbert space by having value -1. But it is hidded from us

Qu. IDDPro Script --- Density states • #grover 4. qp #biamonte@ieee. org # state = cb("001")*cb("001")' state = hadamard(3)*state*hadamard(3)' echo("define a needle in a haystack: ") ####### # Oracle 1 xi = (1, 1) # ---*--# | # --(+)-####### oracle = cu_gate(sigma_x(1), "c 1 c 2 x 3", 3); state = oracle*state*oracle' echo("apply CPS: ") state = kron(hadamard(2), identity(1))*state*kron(hadamard(2), identity(1))' state = kron(sigma_x(2), identity(1))*state*kron(sigma_x(2), identity(1))' state = cu_gate(hadamard(1), "x 2", 3)*state*cu_gate(hadamard(1), "x 2", 3)' state = cu_gate(sigma_x(1), "c 1 x 2", 3)*state*cu_gate(sigma_x(1), "c 1 x 2", 3)' state = cu_gate(hadamard(1), "x 2", 3)*state*cu_gate(hadamard(1), "x 2", 3)' state = kron(sigma_x(2), identity(1))*state*kron(sigma_x(2), identity(1))' state = hadamard(3)*state*hadamard(3

Qu. IDDPro Script --- State Vector state = cb("001") state = hadamard(3)*state echo("define a needle in a haystack: ") ####### # Oracle 1 xi = (1, 1) # ---*--# | # --(+)-####### oracle = cu_gate(sigma_x(1), "c 1 c 2 x 3", 3); state = oracle*state echo("apply CPS: ") state = kron(hadamard(2), identity(1))*state = kron(sigma_x(2), identity(1))*state = cu_gate(hadamard(1), "x 2", 3)*state = cu_gate(sigma_x(1), "c 1 x 2", 3)*state = cu_gate(hadamard(1), "x 2", 3)*state = kron(sigma_x(2), identity(1))*state = hadamard(3)*state

We found Grover!