Gazdasgmatematika 2 Gyakorlat 12 ht Folyamfeladatok Maximlis folyam

Gazdaságmatematika 2. Gyakorlat – 12. hét Folyamfeladatok: Maximális folyam, minimális vágás Készítette: dr. Nagy Noémi

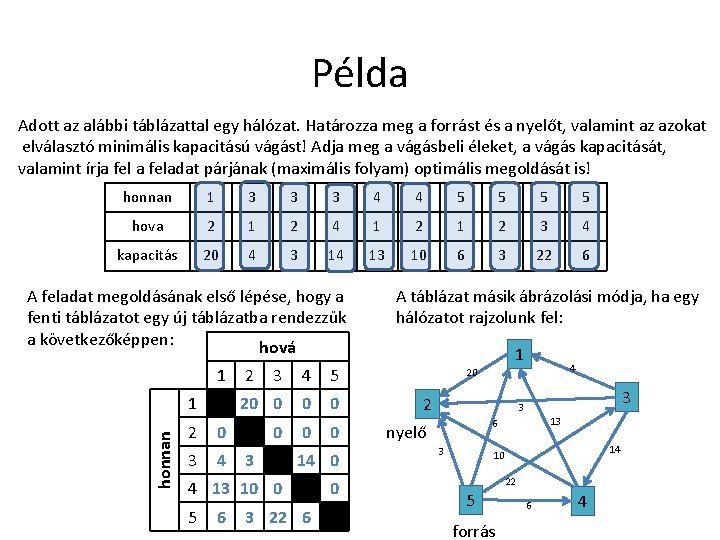
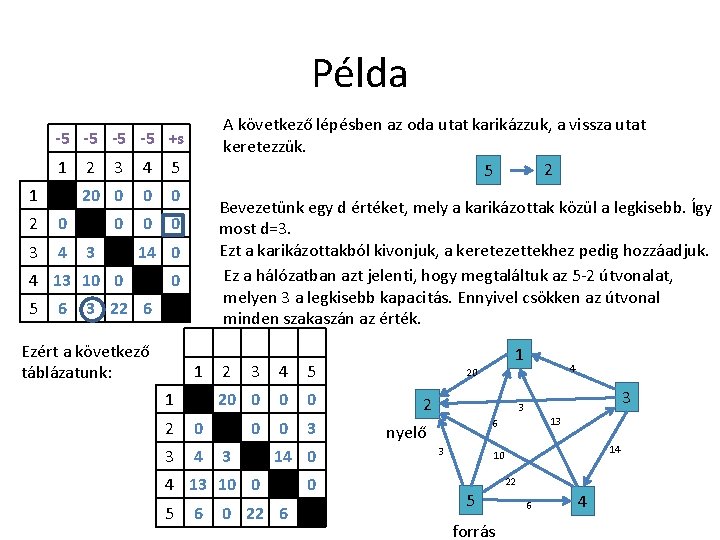
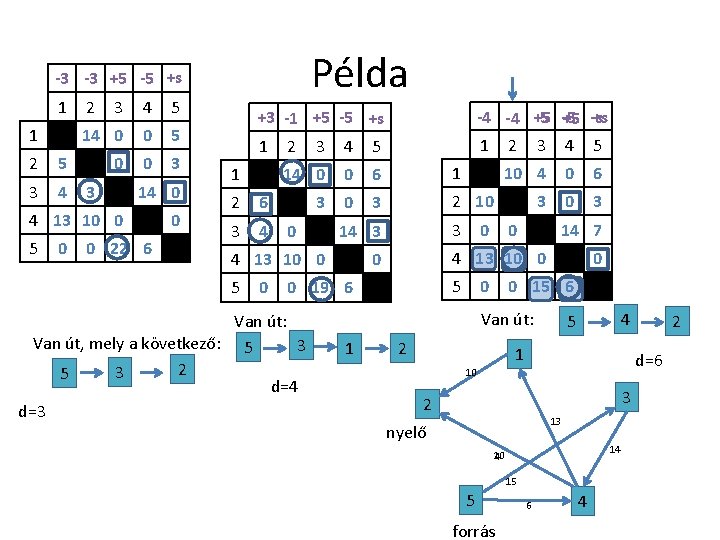
Példa Adott az alábbi táblázattal egy hálózat. Határozza meg a forrást és a nyelőt, valamint az azokat elválasztó minimális kapacitású vágást! Adja meg a vágásbeli éleket, a vágás kapacitását, valamint írja feladat párjának (maximális folyam) optimális megoldását is! honnan 1 3 3 3 4 4 5 5 hova 2 1 2 4 1 2 3 4 kapacitás 20 4 3 14 13 10 6 3 22 6 honnan A feladat megoldásának első lépése, hogy a A nyelő az a pont lesz, ahol a „honnan” sor üres: fenti táblázatot egy új táblázatba rendezzük így a nyelő: 2 a következőképpen: A forrás az a pont, ahol a „hová” oszlop üres: hová így a forrás: 5 1 2 3 4 5 A többi helyre nulla kerül. 1 20 0 2 0 3 4 0 3 0 14 0 4 13 10 0 5 6 0 3 22 6 0

Példa Adott az alábbi táblázattal egy hálózat. Határozza meg a forrást és a nyelőt, valamint az azokat elválasztó minimális kapacitású vágást! Adja meg a vágásbeli éleket, a vágás kapacitását, valamint írja feladat párjának (maximális folyam) optimális megoldását is! honnan 1 3 3 3 4 4 5 5 hova 2 1 2 4 1 2 3 4 kapacitás 20 4 3 14 13 10 6 3 22 6 A feladat megoldásának első lépése, hogy a fenti táblázatot egy új táblázatba rendezzük a következőképpen: hová 1 honnan 1 2 0 3 4 2 3 4 5 20 0 0 0 3 14 0 4 13 10 0 5 6 3 22 6 0 A táblázat másik ábrázolási módja, ha egy hálózatot rajzolunk fel: 1 4 20 2 3 3 13 6 nyelő 3 14 10 22 5 forrás 6 4

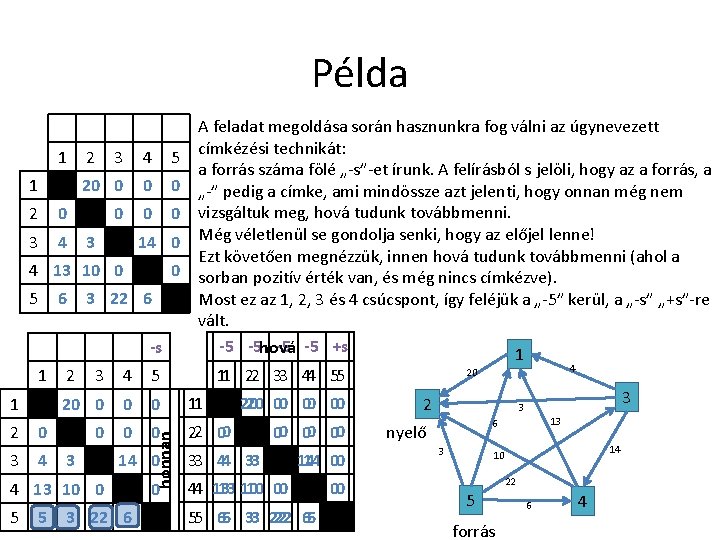
Példa 1 1 2 0 3 4 2 3 4 5 20 0 0 0 3 14 0 4 13 10 0 5 6 0 3 22 6 -s 1 2 0 3 4 2 4 5 20 0 11 0 0 0 22 00 3 14 0 4 13 10 0 5 5 11 22 33 44 55 3 honnan 1 A feladat megoldása során hasznunkra fog válni az úgynevezett címkézési technikát: a forrás száma fölé „-s”-et írunk. A felírásból s jelöli, hogy az a forrás, a „-” pedig a címke, ami mindössze azt jelenti, hogy onnan még nem vizsgáltuk meg, hová tudunk továbbmenni. Még véletlenül se gondolja senki, hogy az előjel lenne! Ezt követően megnézzük, innen hová tudunk továbbmenni (ahol a sorban pozitív érték van, és még nincs címkézve). Most ez az 1, 2, 3 és 4 csúcspont, így feléjük a „-5” kerül, a „-s” „+s”-re vált. -5 -5 hová -5 -5 +s 1 3 22 6 0 20 00 00 00 33 44 33 14 00 14 13 10 10 00 44 13 22 66 55 66 33 22 00 4 20 2 3 3 13 6 nyelő 3 14 10 22 5 forrás 6 4

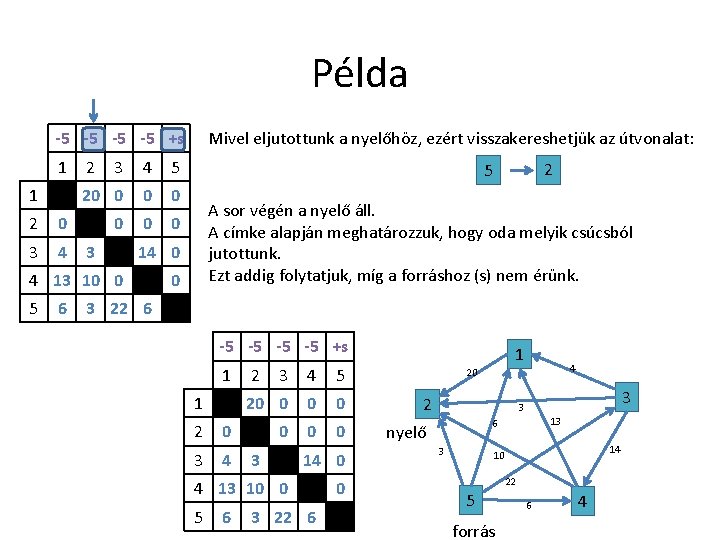
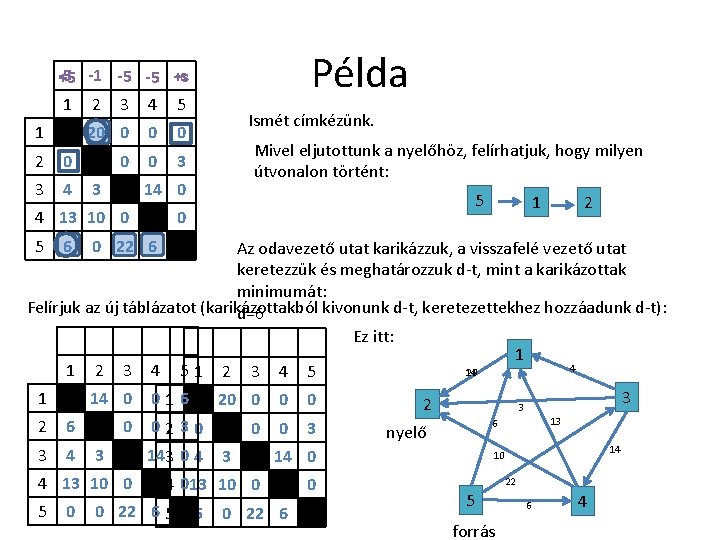
Példa -5 -5 +s 1 1 2 0 3 4 2 3 4 5 20 0 0 0 3 6 2 5 A sor végén a nyelő áll. A címke alapján meghatározzuk, hogy oda melyik csúcsból jutottunk. Ezt addig folytatjuk, míg a forráshoz (s) nem érünk. 14 0 4 13 10 0 5 Mivel eljutottunk a nyelőhöz, ezért visszakereshetjük az útvonalat: 0 3 22 6 -5 -5 +s 1 1 2 0 3 4 2 3 4 5 20 0 0 0 3 14 0 4 13 10 0 5 6 3 22 6 0 1 4 20 2 3 3 13 6 nyelő 3 14 10 22 5 forrás 6 4

Példa A következő lépésben az oda utat karikázzuk, a vissza utat keretezzük. 2 5 -5 -5 +s 1 1 2 0 3 4 2 3 4 5 20 0 0 0 3 14 0 4 13 10 0 5 6 Bevezetünk egy d értéket, mely a karikázottak közül a legkisebb. Így most d=3. Ezt a karikázottakból kivonjuk, a keretezettekhez pedig hozzáadjuk. Ez a hálózatban azt jelenti, hogy megtaláltuk az 5 -2 útvonalat, melyen 3 a legkisebb kapacitás. Ennyivel csökken az útvonal minden szakaszán az érték. 0 3 22 6 Ezért a következő táblázatunk: 1 1 2 0 3 4 2 3 4 5 20 0 0 3 3 14 0 4 13 10 0 5 6 0 22 6 0 1 4 20 2 3 3 13 6 nyelő 3 14 10 22 5 forrás 6 4

Példa -s -5 +5 -1 -5 -5 +s 1 2 3 4 5 1 2 0 3 4 20 0 0 3 3 Ismét címkézünk. Mivel eljutottunk a nyelőhöz, felírhatjuk, hogy milyen útvonalon történt: 14 0 4 13 10 0 5 6 0 22 6 0 3 4 1 2 Az odavezető utat karikázzuk, a visszafelé vezető utat keretezzük és meghatározzuk d-t, mint a karikázottak minimumát: Felírjuk az új táblázatot (karikázottakból kivonunk d-t, keretezettekhez hozzáadunk d-t): d=6 Ez itt: 1 4 1 2 3 4 5 14 20 3 1 14 0 0 1 6 20 0 2 3 3 4 13 10 0 5 0 0230 14 3 0 4 0 3 0 5 0 22 6 0 13 6 nyelő 14 0 13 10 0 0 22 6 5 3 14 10 22 5 forrás 6 4

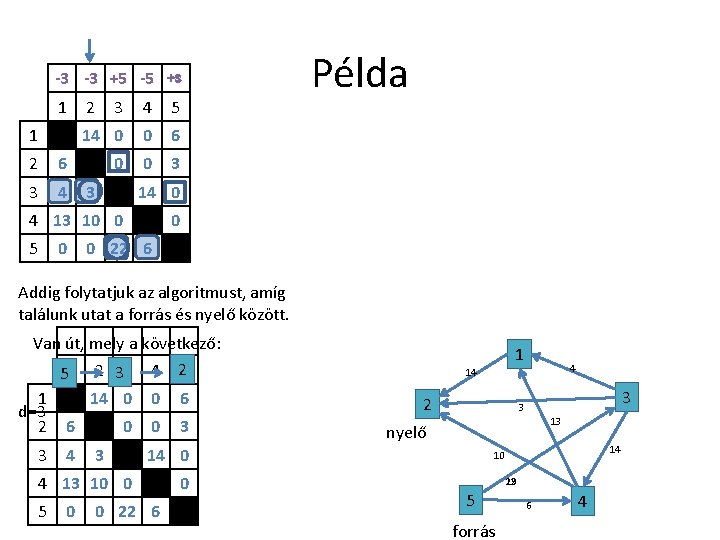
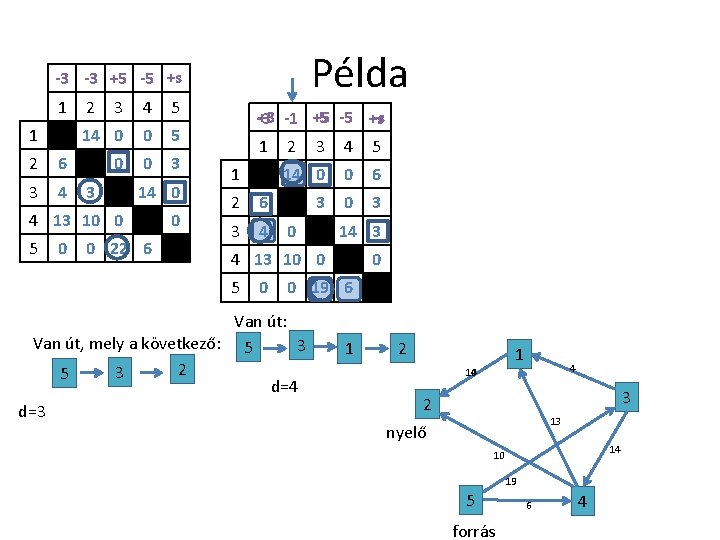
-s -3 -3 +5 -5 -5 +s 1 1 2 6 3 4 2 3 4 5 14 0 0 6 0 0 3 3 14 0 4 13 10 0 5 0 Példa 0 0 22 6 Addig folytatjuk az algoritmust, amíg találunk utat a forrás és nyelő között. Van út, mely a következő: 51 2 33 4 25 1 d=3 2 6 3 4 14 0 0 6 0 0 3 3 0 0 22 6 0 4 14 2 3 3 13 nyelő 14 0 4 13 10 0 5 1 14 10 22 19 5 forrás 6 4

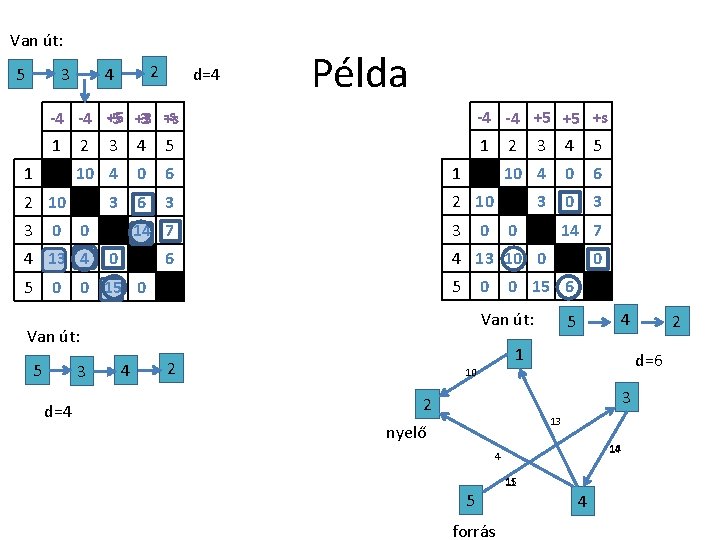
Példa -3 -3 +5 -5 +s 1 1 2 6 3 4 2 3 4 5 14 0 0 5 0 0 3 3 14 0 4 13 10 0 5 0 0 22 6 0 -s +3 -1 +5 -5 -5 +s -3 1 1 2 6 3 4 2 3 4 5 14 0 0 6 3 0 14 3 4 13 10 0 5 0 0 0 19 6 Van út: Van út, mely a következő: 5 3 2 3 5 d=4 d=3 1 2 1 4 10 14 3 2 13 nyelő 14 10 19 15 5 forrás 6 4

Példa -3 -3 +5 -5 +s 1 1 2 5 3 4 2 3 4 5 14 0 0 5 0 0 3 3 14 0 4 13 10 0 5 0 0 22 6 0 -4 -4 +5 -5 -5 +s +5 -s 1 2 3 4 5 +3 -1 +5 -5 +s 1 1 2 6 3 4 2 3 4 5 14 0 0 6 1 3 0 3 2 10 0 4 13 10 0 5 0 3 14 3 0 6 3 0 0 14 7 4 13 10 0 0 5 0 19 6 Van út: Van út, mely a következő: 5 3 2 3 5 d=4 d=3 10 4 0 0 0 15 6 Van út: 1 2 4 5 1 d=6 10 3 2 13 nyelő 14 10 4 15 5 forrás 2 6 4

Van út: 5 2 4 3 d=4 Példa -4 -4 +5 -5 -3 +3 -s +s 1 1 2 3 4 5 10 4 0 6 1 3 6 3 2 10 3 0 0 4 13 4 5 -4 -4 +5 +5 +s 1 2 3 4 5 0 3 14 7 0 0 5 0 15 0 3 d=4 0 6 3 0 14 7 4 13 10 0 6 0 0 0 15 6 Van út: 5 10 4 4 4 5 1 2 d=6 10 3 2 13 nyelő 10 14 4 5 forrás 2 15 11 4

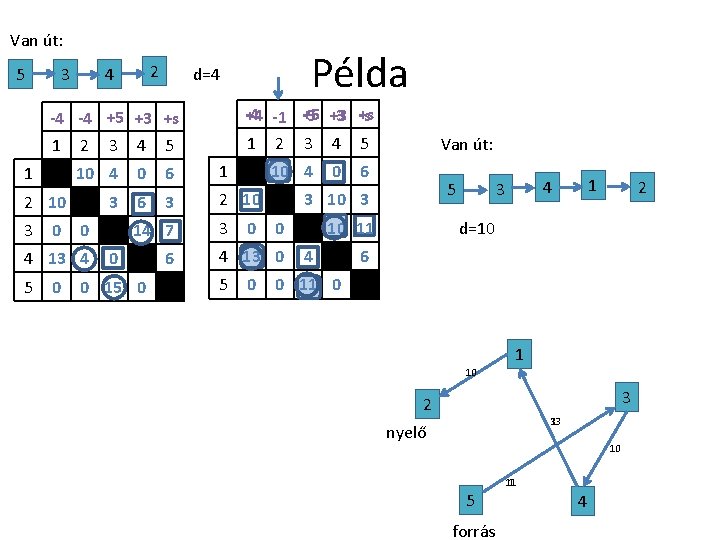
Van út: 5 2 4 3 -4 +s +5 +3 +4 -1 -5 -3 -s 1 2 3 4 5 -4 -4 +5 +3 +s 1 1 2 3 4 5 10 4 0 6 1 3 6 3 2 10 3 0 0 4 13 4 5 0 Példa d=4 14 7 0 0 15 0 6 3 10 4 0 0 6 5 3 10 3 0 4 13 0 5 0 Van út: 10 11 4 3 2 d=10 6 0 11 0 1 10 3 2 13 3 nyelő 10 5 forrás 11 1 4

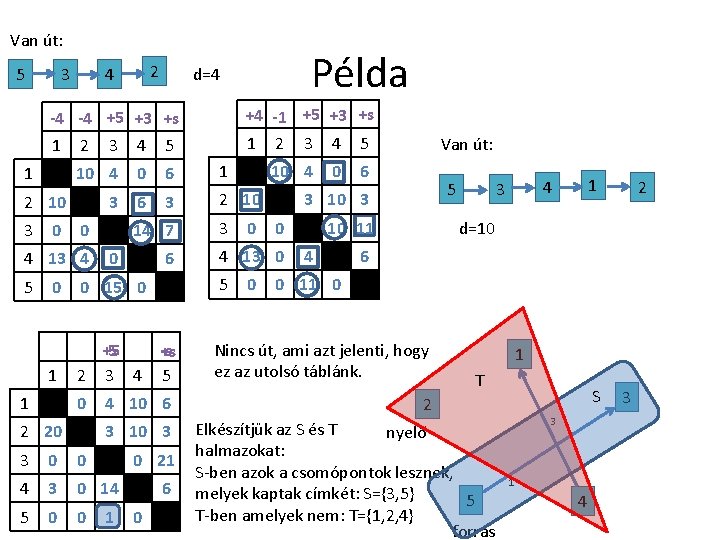
Van út: 5 2 4 3 +4 -1 +5 +3 +s 1 2 3 4 5 -4 -4 +5 +3 +s 1 1 2 3 4 5 10 4 0 6 1 3 6 3 2 10 3 0 0 4 13 4 5 Példa d=4 14 7 0 6 3 10 4 0 6 5 3 10 3 0 4 13 0 10 11 4 5 1 +5 -5 -s +s 2 3 4 5 Nincs út, ami azt jelenti, hogy ez az utolsó táblánk. 2 20 4 10 6 3 10 3 3 0 0 0 21 4 3 0 14 5 0 0 1 6 0 2 6 0 15 0 0 1 4 3 d=10 0 1 0 0 Van út: 0 11 0 1 T S 2 Elkészítjük az S és T nyelő halmazokat: S-ben azok a csomópontok lesznek, melyek kaptak címkét: S={3, 5} 5 T-ben amelyek nem: T={1, 2, 4} forrás 3 1 4 3

Példa A feladat kérdéseinek megválaszolásához szükségünk lesz az eredeti táblázatra és az ebből felírt első táblára, valamint a lépések során meghatározott d értékekre és az utolsó táblára. Ezeket gyűjtjük össze elsőként: A vágásbeli élek meghatározásához az honnan 1 3 3 3 4 4 5 5 hova 2 1 2 4 1 2 3 4 kapacitás 20 4 3 14 13 10 6 3 22 6 Első tábla Utolsó tábla: +5 -5 -5 +s 1 1 2 0 3 4 2 4 5 20 0 1 0 0 0 2 20 3 6 2 3 0 4 10 6 3 0 0 0 4 3 0 14 5 0 0 3 22 6 d=3, d=6, d=3, d=4, d=6, d=4, d=10 4 5 3 10 3 14 0 4 13 10 0 5 1 3 +s 0 21 1 6 0 S és T halmazokra lesz szükségünk: S={3, 5} – utolsó táblában címkézett T={1, 2, 4} – utolsó táblában nem címkézett A táblázatban meg kell keresnünk, mely élek indulnak S-ből és mutatnak T-be, és mennyi ezek kapacitása: 3→ 1 (4), 3 → 2 (3), Ezek tehát a vágásbeli élek. 3→ 4 (14), 5 → 1 (6), A vágás kapacitása a 5 → 2 (3), vágásbeli élek 5 → 4 (6) kapacitásainak összege: 4+3+14+6+3+6=36.

Példa A feladat kérdéseinek megválaszolásához szükségünk lesz az eredeti táblázatra és az ebből felírt első táblára, valamint a lépések során meghatározott d értékekre és az utolsó táblára. Ezeket gyűjtjük össze elsőként: A feladat duálisa, azaz a maximális folyam kiszámítása úgy történik, hogy honnan 1 3 3 3 4 4 5 5 az első táblából kivonjuk az utolsót: hova 2 1 2 4 2 1 2 3 4 kapacitás 20 4 3 14 13 10 6 3 22 6 Első tábla 1 Utolsó tábla: 1 1 2 0 3 4 2 4 5 20 0 1 0 0 0 2 20 3 6 3 3 4 -0 4 3 -0 3 -30 -3 -100 -10 -3 0 -3 14 14 -0 -21 0 -21 5 4 4 13 -3 0 -14 -6 10 10 -0 10 -14 0 4 10 6 5 5 6 -0 6 3 -0 3 2122 -1 6 6 -0 0 4 3 0 14 5 0 0 d=3, d=6, d=3, d=4, d=6, d=4, d=10 +s 3 10 3 0 21 1 6 0 5 20 -0 20 -40 -4 -100 -10 -6 0 -6 3 3 3 22 6 4 4 5 2 14 0 4 13 10 0 5 1 3 11 22 3 3 4 2 2 0 -20 +5 -5 -5 +s 11 0 -6

Példa A feladat kérdéseinek megválaszolásához szükségünk lesz az eredeti táblázatra és az ebből felírt első táblára, valamint a lépések során meghatározott d értékekre és az utolsó táblára. Ezeket gyűjtjük össze elsőként: A feladat duálisa, azaz a maximális folyam kiszámítása úgy történik, hogy honnan 1 3 3 3 4 4 5 5 az első táblából kivonjuk az utolsót: hova 2 1 2 4 2 1 2 3 4 kapacitás 20 4 3 14 13 10 6 3 22 6 Első tábla 1 Utolsó tábla: 1 1 2 0 3 4 2 4 5 20 0 1 0 0 0 2 20 3 6 3 10 3 0 0 0 4 3 0 14 5 0 0 d=3, d=6, d=3, d=4, d=6, d=4, d=10 4 10 10 -14 4 10 6 0 21 1 6 0 5 5 -3 -10 -3 5 0 4 20 -4 -10 -6 3 3 22 6 4 3 +s 2 14 0 4 13 10 0 5 1 3 1 2 2 -20 +5 -5 -5 +s 1 4 6 3 14 -21 -6 3 21 6 A táblázatban a pozitív értékek azt jelentik, hogy például az első és második csúcs között a kapacitásból felhasznált érték 20. A táblázat antiszimmetrikus, a negatív értékek jelentése, hogy „visszafelé” mekkora a folyam kapacitása.

Példa A feladat kérdéseinek megválaszolásához szükségünk lesz az eredeti táblázatra és az ebből felírt első táblára, valamint a lépések során meghatározott d értékekre és az utolsó táblára. Ezeket gyűjtjük össze elsőként: A feladat duálisa, azaz a maximális folyam kiszámítása úgy történik, hogy honnan 1 3 3 3 4 4 5 5 az első táblából kivonjuk az utolsót: hova 2 1 2 4 2 1 2 3 4 kapacitás 20 4 3 14 13 10 6 3 22 6 Első tábla 1 Utolsó tábla: 1 1 2 0 3 4 2 4 5 20 0 1 0 0 0 2 20 3 6 3 10 3 0 0 0 4 3 0 14 5 0 0 d=3, d=6, d=3, d=4, d=6, d=4, d=10 4 10 10 -14 4 10 6 0 21 1 6 0 5 5 -3 -10 -3 -36 5 0 4 20 -4 -10 -6 0 3 3 22 6 4 3 +s 2 14 0 4 13 10 0 5 1 3 1 2 2 -20 +5 -5 -5 +s 1 4 6 3 14 -21 0 3 21 6 -6 0 36 0 0 -36 Ha a sorokban és oszlopokban összegezzük az értékeket, megkapjuk, hogy az adott csúcson mekkora mennyiség megy tovább. Itt is megkapjuk a 36 értéket, mint a minimális vágás esetén. (Ez a d-k összege is)

Megjegyzés Természetesen a feladat megoldásához a táblázatok számítása elegendő, azokat hálózatként ábrázolni nem szükséges. Az mindössze arra szolgált, hogy jobban el tudjuk képzelni, hogy miről szól a feladat. Nagyobb hálózat egyébként sem lenne átlátható. A feladat megoldása során a végrehajtandó teendők a következők: 1. az induló tábla felírása 2. címkézés 3. a forrástól a nyelőhöz vezető út meghatározása 4. d értékének meghatározása 5. új tábla kiszámítása 6. 2 -5. ismétlése, amíg találunk utat a forrás és a nyelő között 7. amikor már nem találunk utat, S és T felírása (címkézett és címkézetlen) 8. az eredeti táblázatból megkeresni, hogy mely élek vezetnek közvetlenül S és T között. Ezek lesznek a vágásbeli élek. 9. A vágás kapacitásának kiszámítása: vágásbeli élek kapacitásainak összege. 10. A maximális folyam felírása: az első és utolsó tábla különbségének meghatározása 11. A maximális folyam értékének meghatározása: a „különbség tábla” sorainak és oszlopainak összegeit kiszámolni. Ugyanezt az értéket kell adnia a számolás során kapott d-k összegének is.