Engineering Economics I Interest and Equivalence Engineering Economics















- Slides: 15

Engineering Economics I Interest and Equivalence

Engineering Economics • Engineering Economics is the application of standard set of equivalence equations in determining the relative economic value of a small set of alternative capital investments that differ in their time streams of costs and benefits. • As a civil engineer you may need to determine the financial feasibility of the project or the most economical design alternative. • The information covered here is needed for the (FE) and the (PE) exams.

Cash Flow Table and Diagram • To illustrate the time stream of costs and benefits. • Receipts are positives and disbursements are negatives • End-of-period convention applies • Time 0 is the present • Arrows in a diagram are not to scale but they represent the relative magnitude. • The sign of the cash flow depends on the view point taken

A person borrowed $10, 000 and has agreed to pay back as shown below 10, 000 Receipts (+) 1, 000 Disbursements (-) 1, 000 11, 000

Simple Interest and Equivalence • Principal: the amount given by the lender to the borrower. • Interest: the payment we provide for the use of money. • Simple annual interest: the interest computed only on the principal outstanding for a year. • The previous example was about 10% simple interest on a $1000 loan for 4 years. • The current arrangement is equivalent to the best arrangement that either part could obtain elsewhere • Equivalence may breakdown if the interest rate is changed.

Compound Interest-Single Payment • Compound interest: computed on both the principal and the interest outstanding for a given time period. • Define: – i: compound interest rate for a period of time expressed as a decimal – n: number of time periods. – P: present amount of money. – F: future amount of money at the end of period n F = P(1+i)n or F = P(F/P, i, n) “the future amount, F, equals the present amount, P, times the factor for F given P compounded at interest rate i for n periods.

• Present worth P can be computed from F the same way: P = F(1+i)-n or P = F (P/F, i, n) • Tables for the factors (P/F, i, n) and (F/P, i, n) are given in Appendix B in Engineering Economy (online). • You do not have to remember the formulas, just remember the factors, e. g: (P/F, i, n). The first term refers to what you want to compute and the second refers to what is invested. • How much will you invest today to receive $1000 after 7 years assuming interest rate of 11%? – P = F (P/F, i, n) = 1000 *(1. 11)-7 = $481. 658 – or from the table page 556: P/F = 0. 4817 – Keep 6 decimal places in your computations

• Rule of 72: – if (i X n = 72), future factor is » 2, money will double • Nominal and effective interest rate – the nominal interest rate for a time period ignores the effect of any subperiod compounding. – effective interest rate takes into account the accumulation of interest: 4% computed quarterly means that the interest is computed and added to the principal every three months. – if r is the nominal interest rate per time period; and m: number of compound subperiods per time period. then effective annual interest rate iy = (1+ )m - 1 – What is the effective annual interest rate of 7% nominal interest compounded monthly? the answer is 7. 23%

Standard Cash Flow Series • To compute the future or present value of periodic payments. • E. g. : 1) what is the present value of a $1000 annual maintenance fees paid for 7 years assuming 5% interest rate? 2) how much do I deposit each year into an account to receive $100, 000 after 15 years if the interest rate is 6%? 3) a dam will cost $10 million every 50 years for renovation purposes. If the interest rate is 10%, how much should we set aside now?

1 - Uniform Series • Present worth formula: (A is the periodic payment) P=A or P = A(P/A, i, n) 0 A n P=? • Capital recovery formula: the opposite A =P or A = P(A/P, i, n) 0 A=? P Answer to question (1) : 1) Use the first formula, the answer is $5786. 37? n

• Compound amount formula: F=A OR F = A(F/A, i, n) 0 A n F=? Sinking fund formula A=F OR A = F(A/F, i, n) 0 A= ? n F Answer to question (2) 2) Using the sinking fund formula: A = $4, 296. 28

2 - Arithmetic Gradient Series • How much should we invest today to provide for the repairs over a period of time given that repair costs increase with time? • Present worth formula: (n-1)G P=G or P = G(P/G, i, n) 0 P=? 2 G G where G is the gradient. Payment at the end of period 1 is 0, period 2 is G, period 3 is 2 G, . . . , period n is (n-1)G. . n

Example Convert the following series to its equivalent future worth, F, when I is 12%. Compute the present worth and then convert it to future worth

3 - Capitalized Cost • When it is necessary to assume that a certain structure or service will provide for ever. E. g. . : highways, pipelines, and dams. • The goal is to compute the amount of money that need to be set aside now to provide a fixed payment at certain intervals, for repairs ? • If we know the annual amount needed (A), the present investment P = A/ i. . . . (1) • If we know the amount needed each set of years (F), 10 million every 50 years for example, we first compute the annual payment A = F(A/F, i, n) then use formula (1) • Example 13 -8

Example A dam initially costs $30 million and must be renovated every 50 years at a cost of $10 million. Interest is 8%. Find the capitalized cost sufficient to construct and maintain the project in perpetuity.
 What is economic equivalence
What is economic equivalence Magnetically equivalent protons
Magnetically equivalent protons Examples of formal equivalence
Examples of formal equivalence Formal equivalent
Formal equivalent Nominal v. real interest rates
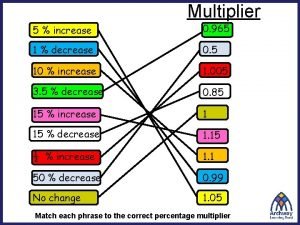
Nominal v. real interest rates 0 965
0 965 Nominal interest rate
Nominal interest rate Dynamic aggregate demand equation
Dynamic aggregate demand equation What is self interest in economics
What is self interest in economics School of business and economics maastricht
School of business and economics maastricht Elements of mathematical economics
Elements of mathematical economics How managerial economics is useful to engineers
How managerial economics is useful to engineers Law of variable proportions in economics
Law of variable proportions in economics Engineering economics and management
Engineering economics and management Euac economics
Euac economics Depreciation in engineering economics
Depreciation in engineering economics