Chapter2 Relations And Functions This Presentation contain The

Chapter-2 Relations And Functions This Presentation contain The following Topics: v. Ordered Pair v Cartesian Product of Sets v. Relations

Ordered Pair : - An ordered pair is a pair of objects taken in a specific order. An ordered pair is written by listing the two members in a specific order, separating them by comma and enclosing the pair in parenthesis. Ex. In the ordered pair (a, b) , a is called the first element or member and b is called the second element or member. Cartesian Product of Two Sets Let A and B be any two non- empty sets , then the set of all ordered pairs (a, b) for all a Є A and b Є B is called the cartesian product of A and B. => A x B = { (a, b) : a Є A and b Є B } Ex. Let A = { 1, 2, 3} and B = { 3, 4} Then A x B = { (1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)} And B x A = { (3, 1), (3, 2), (3, 3), (4, 1), (4, 2), (4, 3)}

From the example we can observe that : (i) A x B ≠ B x A (ii) n(A x B ) = n(A) x n(B) = 3 x 2 = 6 Note : 1) A x B ≠ B x A unless A = B 2) A x B = ɸ , when one or both of A, B are empty sets. 3) If A and B are non- empty finite sets then , n(A x B ) = n(A) x n(B) and n(A x B) = n(B x A ) 4) If A and B are non- empty sets and either A or B is an infinite set, then A x B is also an infinite set. If A, B and C are three non- empty sets then (A x B x C) ={ (a, b, c): aЄ A , b Є B and c Є C } And n(Ax. Bx. C) = n(A) x n(B) x n ( C )

Relations Consider the two sets P = { a, b, c} and Q = {Ali, Binoy, Bhanu, Chandra} Then P x Q = {(a, Ali), (a, Binoy), (a, Bhanu), ……. (c, Chandra } = 12 ordered pairs. Now we can obtain a subset of Px. Q by introducing a relation R between P and Q such That R = { (x, y): x is the first letter of the name y, x Є P , y Є Q} Then R = { (a, Ali), (b, Binoy), (b, Bhanu), (c, Chandra)} Definition : - A relation R from a non-empty set A to a nonempty set B is a subset of the cartesian product A x B. The subset is derived by describing the relationship between the first element and second element of the ordered pairs in A x B.

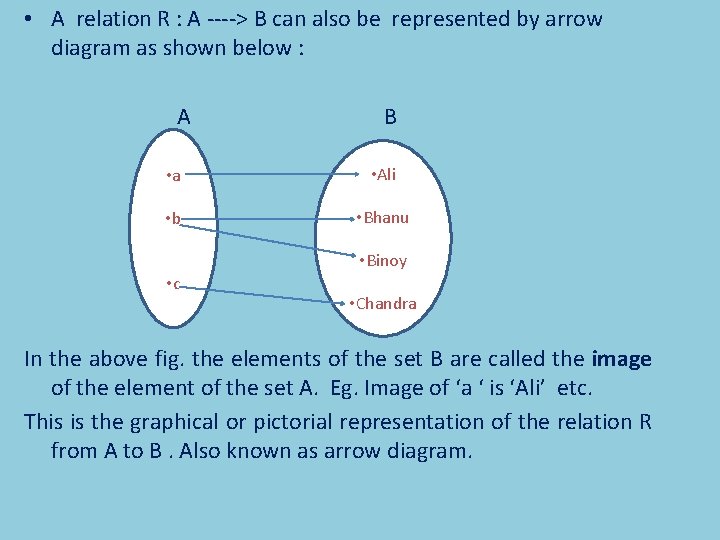
• A relation R : A ----> B can also be represented by arrow diagram as shown below : A B • a • Ali • b • Bhanu • Binoy • c • Chandra In the above fig. the elements of the set B are called the image of the element of the set A. Eg. Image of ‘a ‘ is ‘Ali’ etc. This is the graphical or pictorial representation of the relation R from A to B. Also known as arrow diagram.

From the relation R : A ---> B we have three most important terms, which are as follows : 1. Domain : - The set of all first elements of the ordered pairs (a, b) in the relation R is called the domain of the relation R. For example in the above relation { a, b, c} is the domain. 2. Range : - The set of all second elements of the ordered pairs (a, b) in the relation R is called the range of the relation R. for example in the above relation { Ali, Binoy, Bhanu, Chandra} is the range. 3. Co-domain : - The second set as a whole is called the codomain. Eg. In the above relation set B is co-domain. So we can say that “range is the subset of co-domain”.

Some Examples of Relations Example 1. Let A = { 1, 2, 3, 4, 5, 6}. Find the relation R from A to A defined by R = { (x, y) : y = x+1, x , y Є A } i. Represent this relation by arrow diagram. ii. Find Domain, Range and Co-domain, of the relation. Solution : we have given the set A = { 1, 2, 3, 4, 5, 6} and the relation R = { (x, y): y = x+1, x, y Є A }. From this we get R = { (1, 2), (2, 3), (3, 4), (4, 5), (5, 6)} The arrow diagram is shown bellow from the fig. we can see that • 1 Domain = { 1, 2, 3, 4, 5, 6} • 2 • 3 Range = { 2, 4, 5, 6} • 4 Co-domain = { 1, 2, 3, 4, 5, 6} • 5 • 6

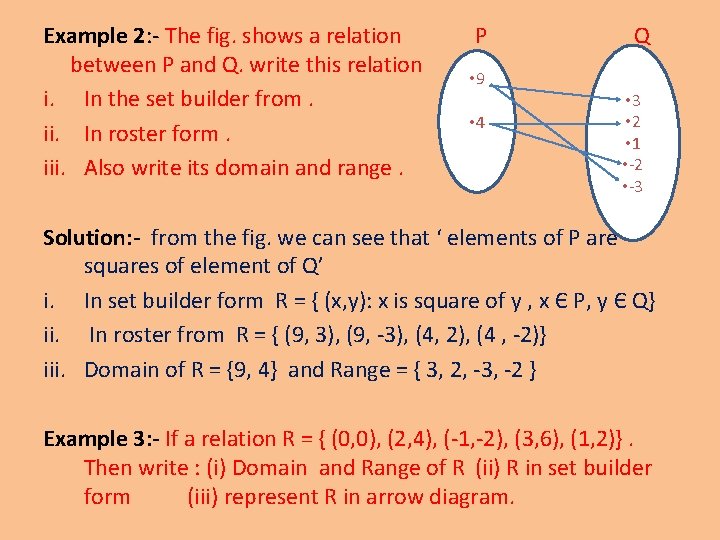
Example 2: - The fig. shows a relation between P and Q. write this relation i. In the set builder from. ii. In roster form. iii. Also write its domain and range. P • 9 • 4 Q i. ii I • 3 • 2 • 1 • -2 • -3 Solution: - from the fig. we can see that ‘ elements of P are squares of element of Q’ i. In set builder form R = { (x, y): x is square of y , x Є P, y Є Q} ii. In roster from R = { (9, 3), (9, -3), (4, 2), (4 , -2)} iii. Domain of R = {9, 4} and Range = { 3, 2, -3, -2 } Example 3: - If a relation R = { (0, 0), (2, 4), (-1, -2), (3, 6), (1, 2)}. Then write : (i) Domain and Range of R (ii) R in set builder form (iii) represent R in arrow diagram.

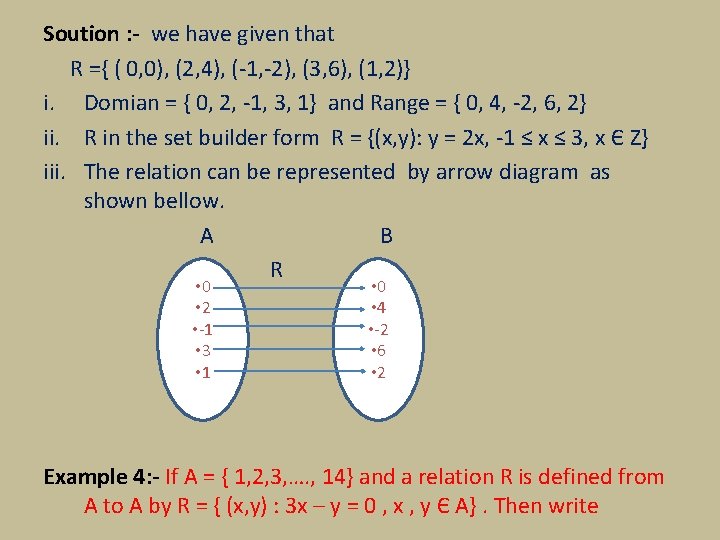
Soution : - we have given that R ={ ( 0, 0), (2, 4), (-1, -2), (3, 6), (1, 2)} i. Domian = { 0, 2, -1, 3, 1} and Range = { 0, 4, -2, 6, 2} ii. R in the set builder form R = {(x, y): y = 2 x, -1 ≤ x ≤ 3, x Є Z} iii. The relation can be represented by arrow diagram as shown bellow. A B R • 0 • 2 • -1 • 3 • 1 • 0 • 4 • -2 • 6 • 2 Example 4: - If A = { 1, 2, 3, …. , 14} and a relation R is defined from A to A by R = { (x, y) : 3 x – y = 0 , x , y Є A}. Then write

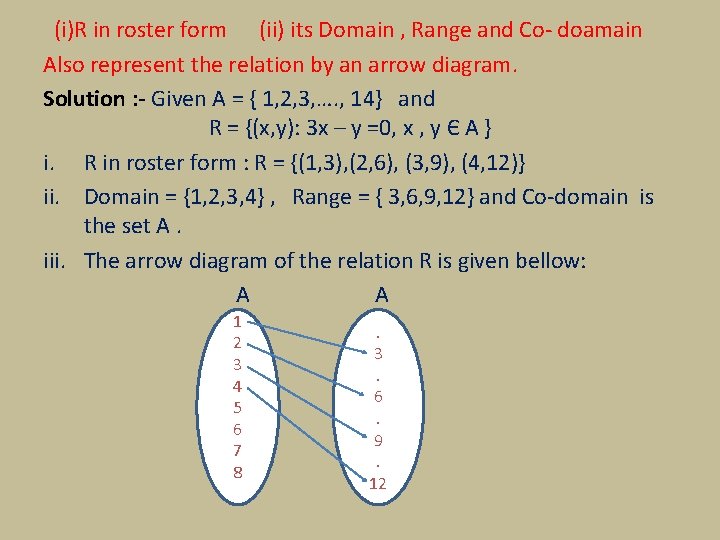
(i)R in roster form (ii) its Domain , Range and Co- doamain Also represent the relation by an arrow diagram. Solution : - Given A = { 1, 2, 3, …. , 14} and R = {(x, y): 3 x – y =0, x , y Є A } i. R in roster form : R = {(1, 3), (2, 6), (3, 9), (4, 12)} ii. Domain = {1, 2, 3, 4} , Range = { 3, 6, 9, 12} and Co-domain is the set A. iii. The arrow diagram of the relation R is given bellow: A A 1 2 3 4 5 6 7 8 . 3. 6. 9. 12