Analysis of Algorithms Input Algorithm Output An algorithm

Analysis of Algorithms Input Algorithm Output An algorithm is a step-by-step procedure for solving a problem in a finite amount of time. Spring 2003 CS 315

Theoretical Analysis Uses a high-level description of the algorithm instead of an implementation Characterizes running time as a function of the input size, n. Takes into account all possible inputs Allows us to evaluate the speed of an algorithm independent of the hardware/software environment Spring 2003 CS 315 2

Where do they get these things? Pseudocode Details Method call Control flow n n n if … then … [else …] while … do … repeat … until … for … do … Indentation replaces braces Method declaration Algorithm method (arg [, arg…]) Input … Output … Spring 2003 CS 315 var. method (arg [, arg…]) Return value return expression Expressions ¬ Assignment (like in Java) Equality testing (like in Java) n 2 Superscripts and other mathematical formatting allowed 3

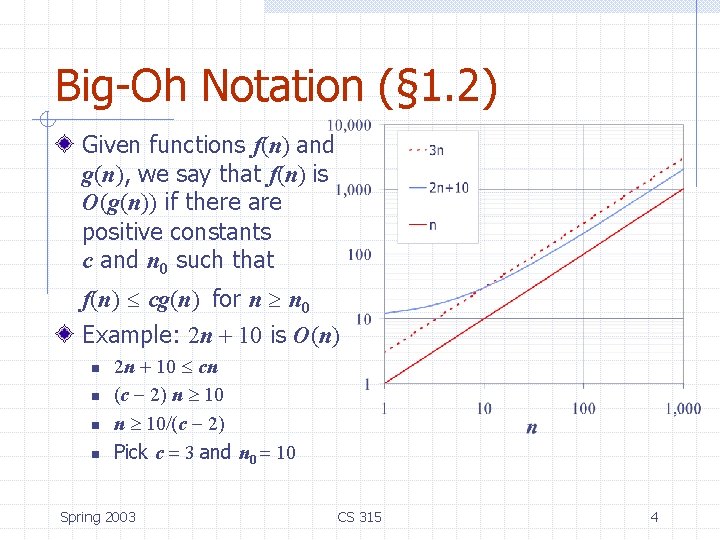
Big-Oh Notation (§ 1. 2) Given functions f(n) and g(n), we say that f(n) is O(g(n)) if there are positive constants c and n 0 such that f(n) cg(n) for n n 0 Example: 2 n + 10 is O(n) n n 2 n + 10 cn (c 2) n 10/(c 2) Pick c 3 and n 0 10 Spring 2003 CS 315 4

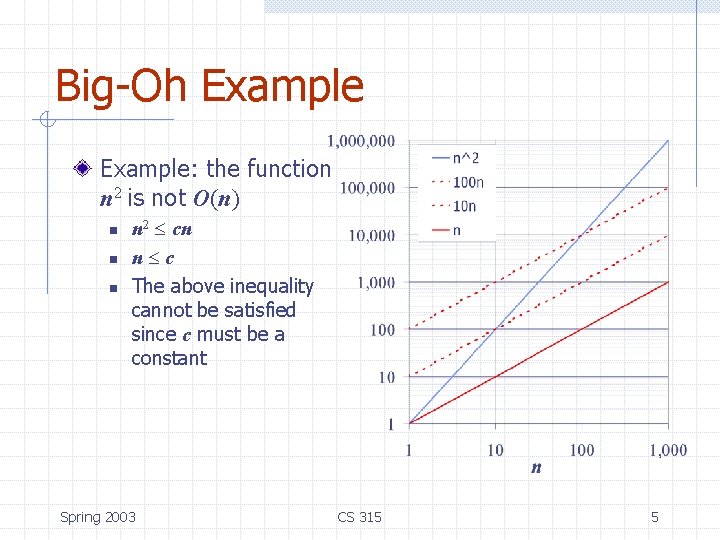
Big-Oh Example: the function n 2 is not O(n) n n 2 cn n c The above inequality cannot be satisfied since c must be a constant Spring 2003 CS 315 5

More Big-Oh Examples n 7 n-2 is O(n) need c > 0 and n 0 1 such that 7 n-2 c • n for n n 0 this is true for c = 7 and n 0 = 1 n 3 n 3 + 20 n 2 + 5 is O(n 3) need c > 0 and n 0 1 such that 3 n 3 + 20 n 2 + 5 c • n 3 for n n 0 this is true for c = 4 and n 0 = 21 n 3 log n + log log n is O(log n) need c > 0 and n 0 1 such that 3 log n + log n c • log n for n n 0 this is true for c = 4 and n 0 = 2 Spring 2003 CS 315 6

Big-Oh Rules If is f(n) a polynomial of degree d, then f(n) is O(nd), i. e. , 1. 2. Drop lower-order terms Drop constant factors Use the smallest possible class of functions n Say “ 2 n is O(n)” instead of “ 2 n is O(n 2)” Use the simplest expression of the class n Spring 2003 Say “ 3 n + 5 is O(n)” instead of “ 3 n + 5 is O(3 n)” CS 315 7

Asymptotic Algorithm Analysis The asymptotic analysis of an algorithm determines the running time in big-Oh notation To perform the asymptotic analysis n n We find the worst-case number of primitive operations executed as a function of the input size We express this function with big-Oh notation Example: n n We determine that algorithm array. Max executes at most 6 n 3 primitive operations We say that algorithm array. Max “runs in O(n) time” Since constant factors and lower-order terms are eventually dropped anyhow, we can disregard them when counting primitive operations Spring 2003 CS 315 8

Relatives of Big-Oh big-Omega n f(n) is (g(n)) if there is a constant c > 0 and an integer constant n 0 1 such that f(n) c • g(n) for n n 0 big-Theta n f(n) is (g(n)) if there are constants c’ > 0 and c’’ > 0 and an integer constant n 0 1 such that c’ • g(n) f(n) c’’ • g(n) for n n 0 little-oh n f(n) is o(g(n)) if, for any constant c > 0, there is an integer constant n 0 0 such that f(n) c • g(n) for n n 0 little-omega n f(n) is (g(n)) if, for any constant c > 0, there is an integer constant n 0 0 such that f(n) c • g(n) for n n 0 Spring 2003 CS 315 9

Intuition for Asymptotic Notation Big-Oh n f(n) is O(g(n)) if f(n) is asymptotically less than or equal to g(n) big-Omega n f(n) is (g(n)) if f(n) is asymptotically greater than or equal to g(n) big-Theta n f(n) is (g(n)) if f(n) is asymptotically equal to g(n) little-oh n f(n) is o(g(n)) if f(n) is asymptotically strictly less than g(n) little-omega n f(n) is (g(n)) if is asymptotically strictly greater than g(n) Spring 2003 CS 315 10

Example Uses of the Relatives of Big-Oh n 5 n 2 is (n 2) n f(n) is (g(n)) if there is a constant c > 0 and an integer constant n 0 1 such that f(n) c • g(n) for n n 0 let c = 5 and n 0 = 1 5 n 2 is (n) n f(n) is (g(n)) if there is a constant c > 0 and an integer constant n 0 1 such that f(n) c • g(n) for n n 0 let c = 1 and n 0 = 1 5 n 2 is (n) f(n) is (g(n)) if, for any constant c > 0, there is an integer constant n 0 0 such that f(n) c • g(n) for n n 0 need 5 n 02 c • n 0 given c, the n 0 that satifies this is n 0 c/5 0 Spring 2003 CS 315 11

Graham Scan Sort points in radial order, scan through them If fewer than two points in H, add point p to H If p forms left turn with last two points in H, add p to H If neither of the above two, remove last point from H and repeat test for p. Spring 2003 CS 315 12

Graham Scan Running Time Takes O(n) time to find anchor Takes O(n log n) to sort radially Now, for each point p in the list (i. e. each iteration) we either add a point or take one off the list. Since a point cannot be added or subtracted more than once, we have at most 2 n operations. Total run time O(n) + O(n log n) + O(n) = O(n log n). Spring 2003 CS 315 13