9 2 Analysing Rational Functions Math 30 1

9. 2 Analysing Rational Functions Math 30 -1 1

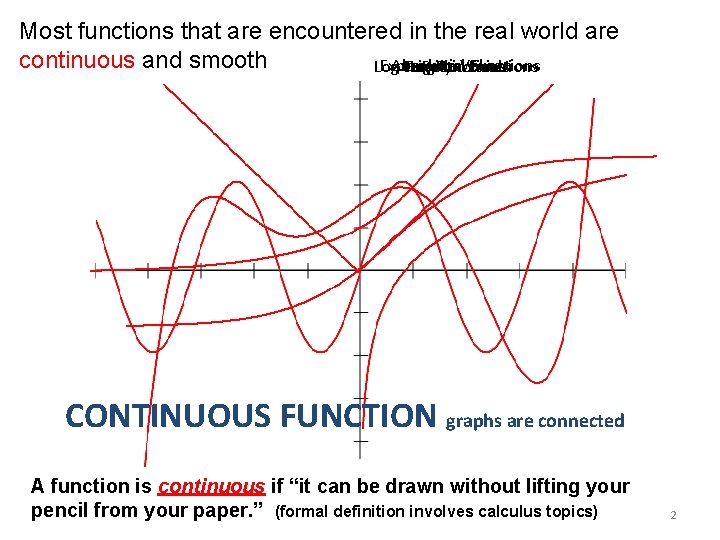
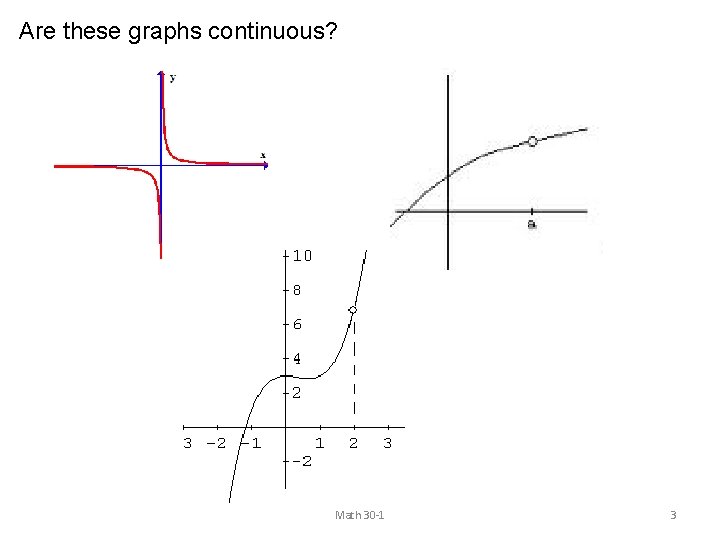
Most functions that are encountered in the real world are continuous and smooth Exponential Absolute Value Functions Log Functions Trig Logistic Polynomials Functions CONTINUOUS FUNCTION graphs are connected A function is continuous if “it can be drawn without lifting your pencil from your paper. ” (formal definition involves calculus topics) 2

Are these graphs continuous? Math 30 -1 3

Discontinuous Function graphs are not connected Many rational functions are discontinuous functions, meaning their graphs contain one or more jumps, breaks, or holes. This occurs at an excluded value, or non-permissible value of the variable. A location on the graph where you must lift your pencil is called a discontinuity. The location is described using the value of x. Breaks in continuity can take 2 forms: A vertical asymptote (line which the function approaches but does not intersect) A point discontinuity (a “hole” in the curve of the function, represented with an open circle) Math 30 -1 4

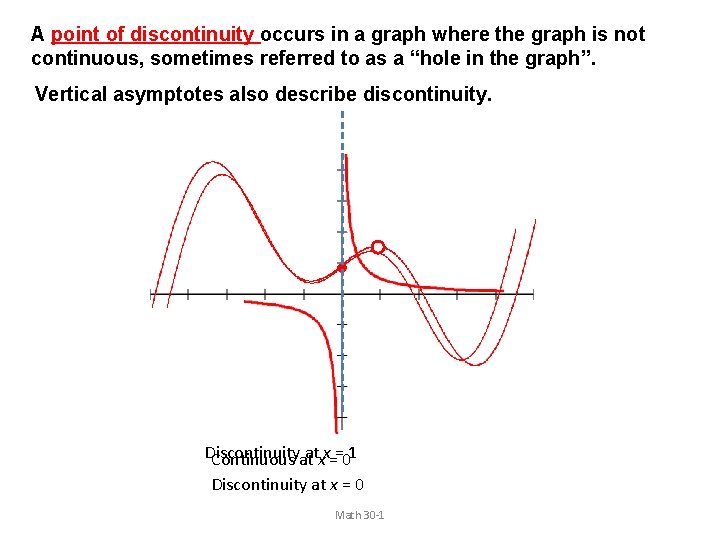
A point of discontinuity occurs in a graph where the graph is not continuous, sometimes referred to as a “hole in the graph”. Vertical asymptotes also describe discontinuity. Discontinuity Continuous atatxx==01 Discontinuity at x = 0 Math 30 -1

Discontinuity from the Function Equation For rational functions, discontinuities can be found by determining where the denominator is equal to zero, the non-permissible values for the variable. The rational function has a point of discontinuity or a vertical asymptote for each real zero of Q(x). If P(x) and Q(x) has no common zeros, then the graph has a vertical asymptote for each zero of Q(x). If P(x) and Q(x) have a common zero, then there is a hole at each of the common zeros. Examine the factors of the numerator and denominator to determine locations of asymptotes and zeros. Math 30 -1 6

Finding Breaks in Continuity • Factor the numerator and denominator, then determine the excluded value from the domain Hole at x=c • If the excluded value comes from a factor that is in BOTH the numerator and denominator, this will cause a point discontinuity (hole) • If the excluded value comes from a factor that is ONLY in the denominator, there will be a vertical asymptote at this excluded value Math 30 -1 Vertical Asymptote at x=c 7

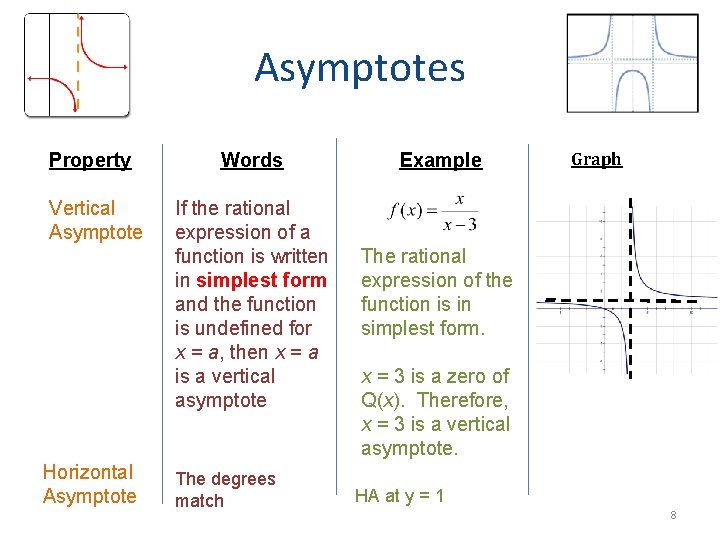
Asymptotes Property Vertical Asymptote Horizontal Asymptote Words If the rational expression of a function is written in simplest form and the function is undefined for x = a, then x = a is a vertical asymptote The degrees match Example Graph The rational expression of the function is in simplest form. x = 3 is a zero of Q(x). Therefore, x = 3 is a vertical asymptote. HA at y = 1 8

Point Discontinuity Property Point Discontinuity Words If the original function is undefined for x = a but the rational expression of the function in simplest form is defined for x = a, then there is a hole in the graph at x = a. Example The original function is undefined for x = – 2. However, the simplified function is defined for x = – 2. Therefore there is a hole at x = – 2. Math 30 -1 Model The height of the hole at x = – 2 can be found by subbing into the simplified function. 9

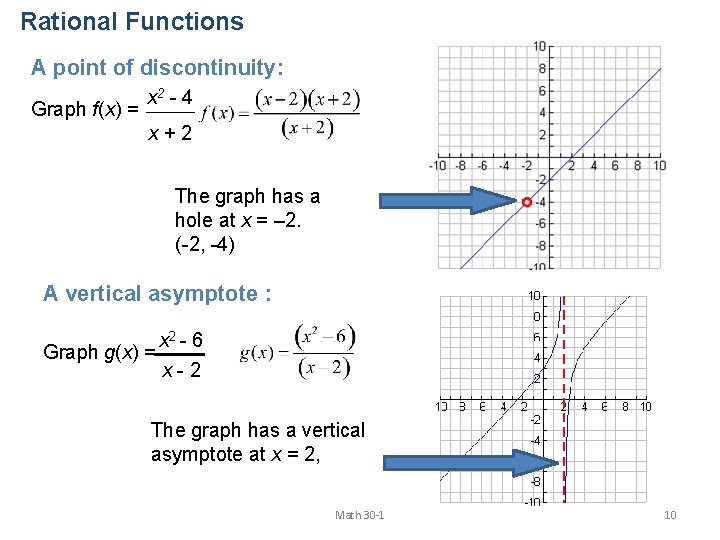
Rational Functions A point of discontinuity: Graph f(x) = x 2 - 4 x+2 The graph has a hole at x = – 2. (-2, -4) A vertical asymptote : Graph g(x) = x 2 - 6 x-2 The graph has a vertical asymptote at x = 2, Math 30 -1 10

Rational Functions Determine the equations of any vertical asymptotes and the values of x for any holes in the graph of The function is undefined for x = 1 and x = 5. Factor the numerator and denominator of the rational expression. 1 1 x – 1 is a factor that is common to both the numerator and the denominator. x = 5 is a vertical asymptote, x = 1 is a hole in the graph (1, -1/2) HA at y = 1 Math 30 -1 11

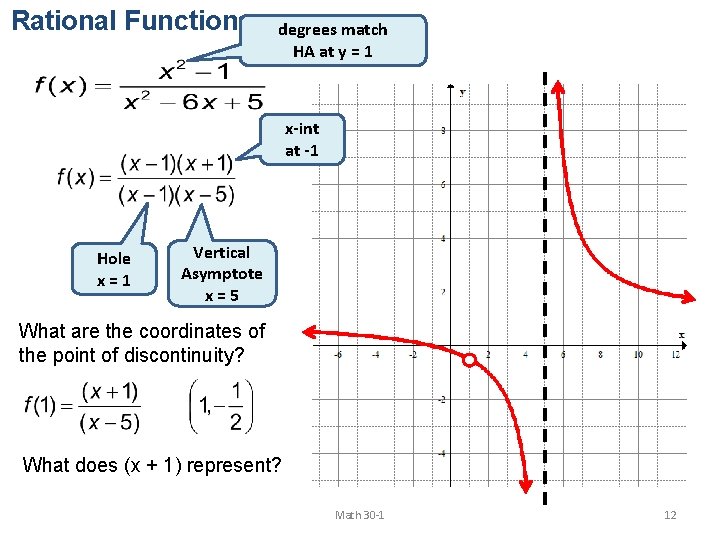
Rational Functions degrees match HA at y = 1 x-int at -1 Hole x=1 Vertical Asymptote x=5 What are the coordinates of the point of discontinuity? What does (x + 1) represent? Math 30 -1 12

Analysing Rational Functions from the Equation Determine the equations of any vertical asymptotes, the coordinates for any holes in each graph, and the x- intercept. Vertical Asymptotes at x = 1 and at x= – 3 HA at y = 0 x- intercept at x=2 Vertical Asymptote at x = – 3 Horizontal Asymptote at y = 0 Hole at x = 2 (2, 1/5) Vertical Asymptote at x = – 5 Math 30 -1 Hole at x = – 3 (-3, -3) x-intercept at x = 3 13

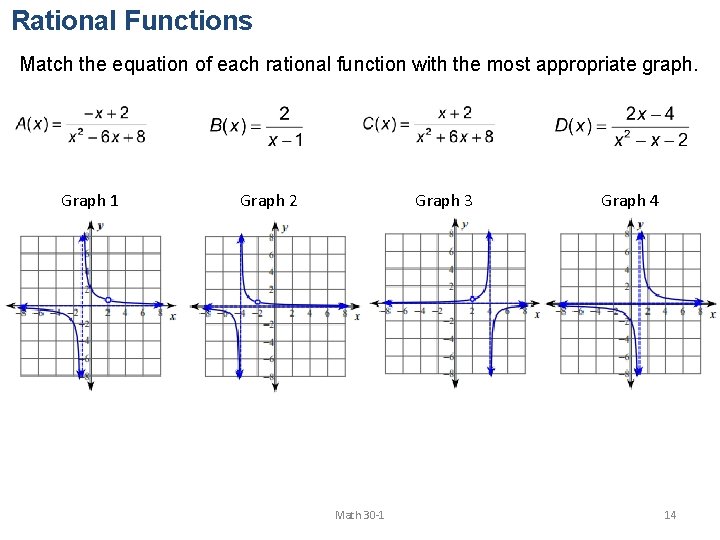
Rational Functions Match the equation of each rational function with the most appropriate graph. Graph 1 Graph 2 Graph 3 Math 30 -1 Graph 4 14

Rational Functions (Multiple Choice) 1. If function f is defined by A. B. C. D. , then at x = 3 The graph of f has a vertical asymptote The graph of f has a hole on the x-axis f(x) = 0 The graph of f has a hole at the point (3, 2) 2. Which of the following functions has a hole at (1, 4)? Math 30 -1 15

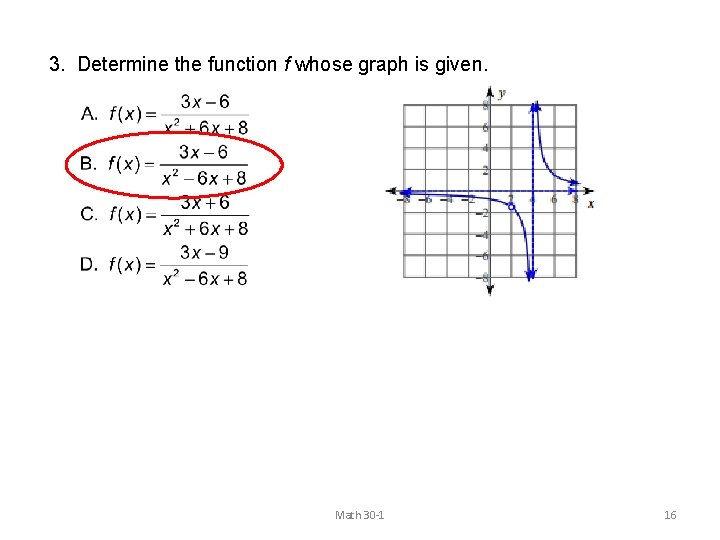
3. Determine the function f whose graph is given. Math 30 -1 16

Page 451 1, 3, 4, 5, 6, 7 a, 8 12, 13, model a situation 13 Math 30 -1 17