8 5 Law of Sines The Law of

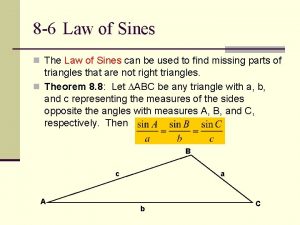
8. 5 Law of Sines

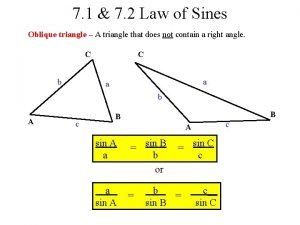
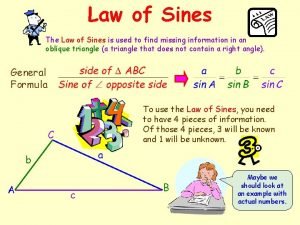
� The Law of Sines and eventually the Law of Cosines, are two formulas that allow us to find angle measurements and distances of triangles that are not right triangles. � The Law of Sines can be used if you know the measures of 2 angles and a side, or you know two sides and a non-included angle. � AAS, ASA, or SSA. These are the orientations of information that will allow you to use the Law of Sines.

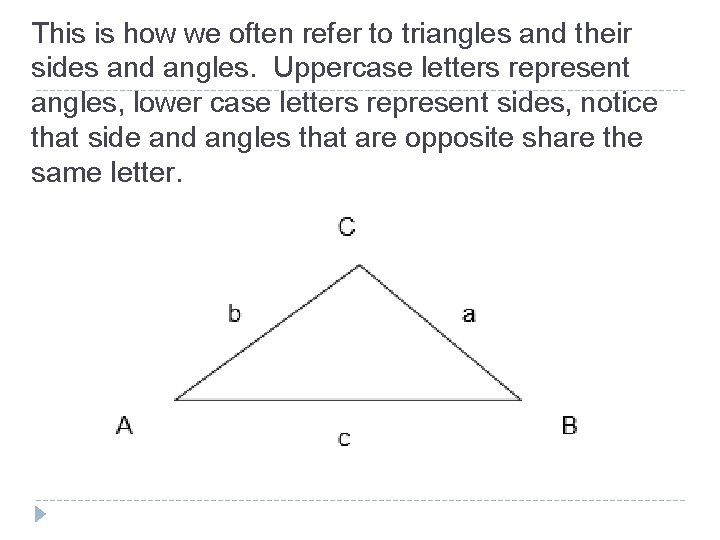
This is how we often refer to triangles and their sides and angles. Uppercase letters represent angles, lower case letters represent sides, notice that side and angles that are opposite share the same letter.

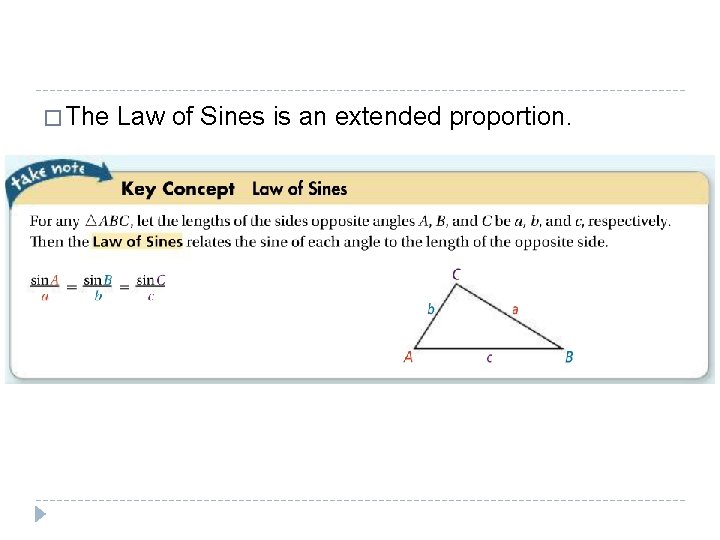
� The Law of Sines is an extended proportion.

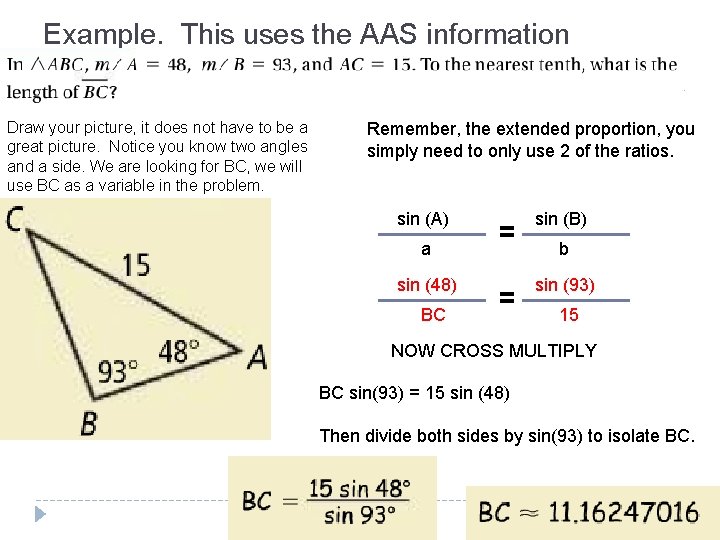
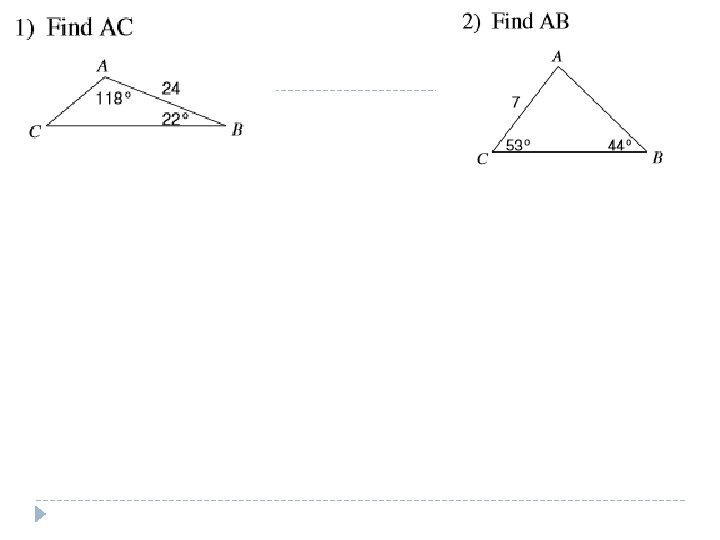
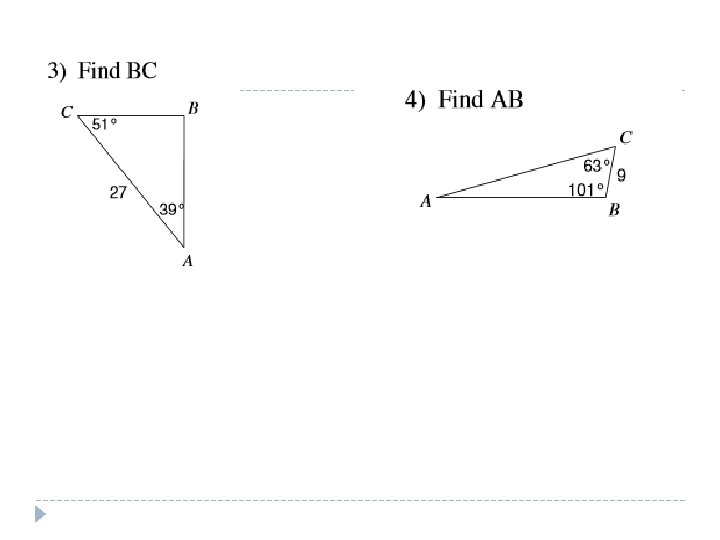
Example. This uses the AAS information Draw your picture, it does not have to be a great picture. Notice you know two angles and a side. We are looking for BC, we will use BC as a variable in the problem. Remember, the extended proportion, you simply need to only use 2 of the ratios. sin (A) a sin (48) BC = sin (B) = sin (93) b 15 NOW CROSS MULTIPLY BC sin(93) = 15 sin (48) Then divide both sides by sin(93) to isolate BC.

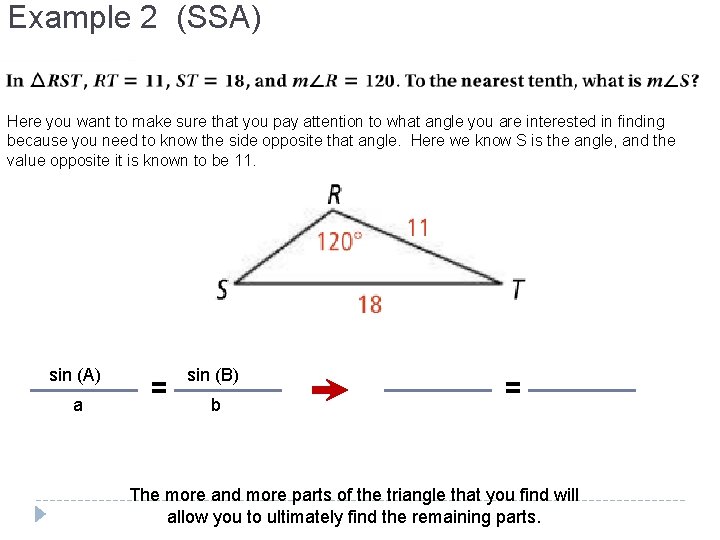
Example 2 (SSA) Here you want to make sure that you pay attention to what angle you are interested in finding because you need to know the side opposite that angle. Here we know S is the angle, and the value opposite it is known to be 11. sin (A) a = sin (B) b = The more and more parts of the triangle that you find will allow you to ultimately find the remaining parts.

AMBIGUITY � Sometimes when given a triangle with SSA the law of sines has an issue dealing with it. When looking at a SSA case we need to take into account that the information we find may lead us to 1 possible triangle, 2 possible triangles, or no possible triangles given the initial data. � This is referred to as an AMBIGUOUS CASE. Ambiguous refers to the notion that a particular situation is open to two or more interpretations. Example, if I told you that I know a person that is named Pat, can you identify their gender? This would be ambiguous, you can make 2 different interpretations of the name.

� Here is an example of the ambiguous case which remember arises when you have SSA. Here we can determine m<B=48. 3 degrees. That means one triangle could consist of angles of 58, 48. 3, and 73. 7 degrees. Because it is SSA we need to verify that there is not a second triangle that could be created, so we take the supplement of the angle we found (48. 3) and the supplement would be 180 -48. 3=131. 7. So potentially angle B could be 131. 7, but if we add the known angle of 58 degrees to that we violate the triangle sum theorem, therefore a second triangle cannot be created and we have one unique triangle with those

Try another one (SSA) Here we can determine that m<B=33. 2 Thus we could have a triangle with measurements of 20, 33. 2, and 126. 8 degrees. However it is SSA so lets see if the supplement of <B will also create a triangle. 180 -33. 2=146. 8. So potentially m<B=146. 8. We need to make sure that this does not violate the triangle sum theorem since we know that m<A=20. 146. 8+20=166. 8, which leaves room in the triangle sum theorem for m<C=13. 2. Thus we have another triangle with those angle measurements.

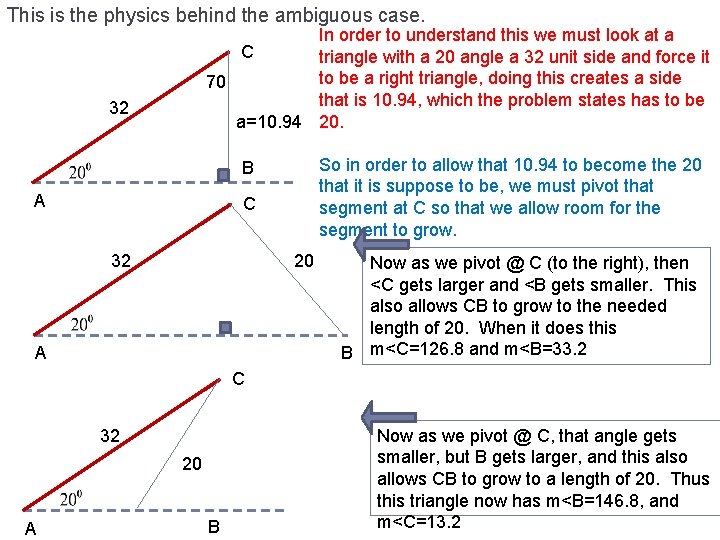
This is the physics behind the ambiguous case. In order to understand this we must look at a C triangle with a 20 angle a 32 unit side and force it to be a right triangle, doing this creates a side 70 that is 10. 94, which the problem states has to be a=10. 94 20. 32 So in order to allow that 10. 94 to become the 20 that it is suppose to be, we must pivot that segment at C so that we allow room for the segment to grow. B A C 20 32 A Now as we pivot @ C (to the right), then <C gets larger and <B gets smaller. This also allows CB to grow to the needed length of 20. When it does this B m<C=126. 8 and m<B=33. 2 C 32 20 A B Now as we pivot @ C, that angle gets smaller, but B gets larger, and this also allows CB to grow to a length of 20. Thus this triangle now has m<B=146. 8, and m<C=13. 2

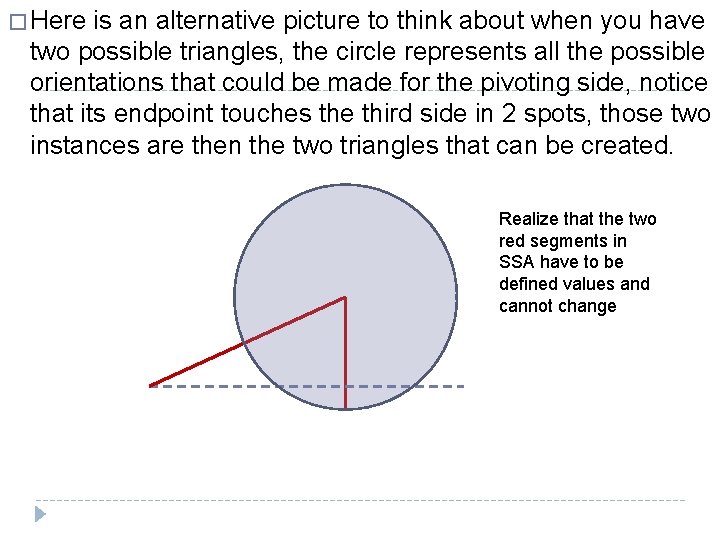
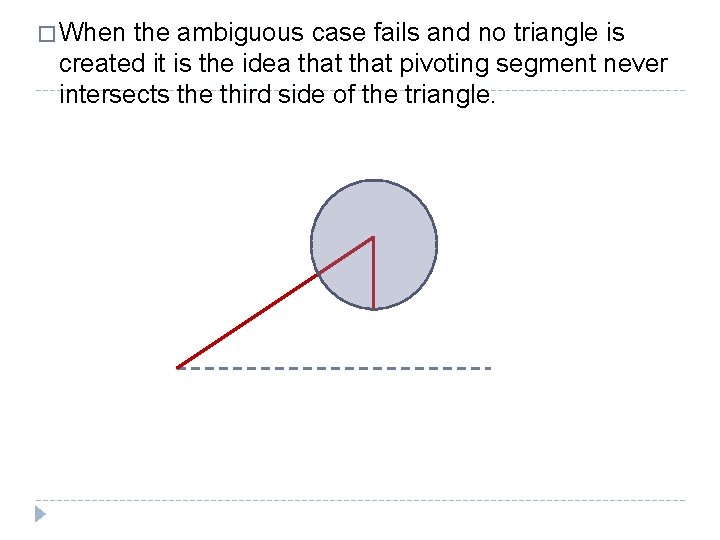
� Here is an alternative picture to think about when you have two possible triangles, the circle represents all the possible orientations that could be made for the pivoting side, notice that its endpoint touches the third side in 2 spots, those two instances are then the two triangles that can be created. Realize that the two red segments in SSA have to be defined values and cannot change

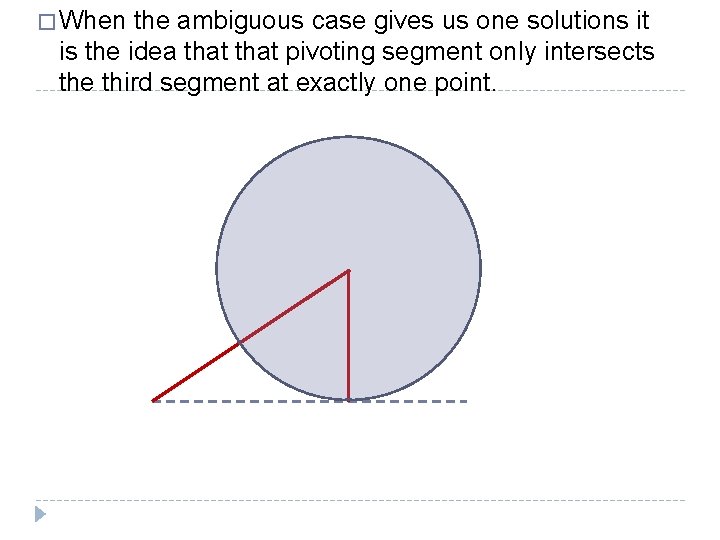
� When the ambiguous case gives us one solutions it is the idea that pivoting segment only intersects the third segment at exactly one point.

� When the ambiguous case fails and no triangle is created it is the idea that pivoting segment never intersects the third side of the triangle.

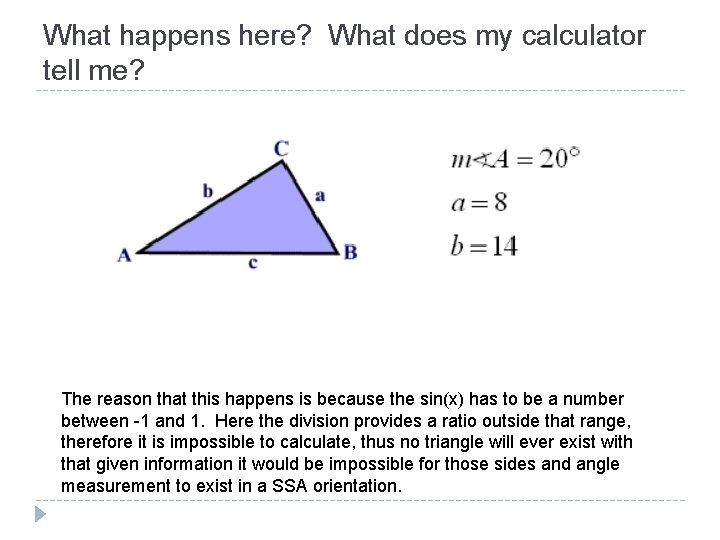
What happens here? What does my calculator tell me? The reason that this happens is because the sin(x) has to be a number between -1 and 1. Here the division provides a ratio outside that range, therefore it is impossible to calculate, thus no triangle will ever exist with that given information it would be impossible for those sides and angle measurement to exist in a SSA orientation.