zyinelemeliRecursive Algoritma Tasarm erik Tanm Tasarm Analiz 1

Özyinelemeli(Recursive) Algoritma Tasarımı • İçerik – Tanım – Tasarım – Analiz 1

Özyinelemeli(Recursive) Yordam • Tanım: Özyinelemeli yordam doğrudan veya dolaylı olarak kendisini çağıran yordamdır. • Gerçek hayatta kullanılan örnekler: – Dizindeki dosyalar üzerinde dolaşma – Programlama dilleri v. b. • Özyineleme güçlü bir problem çözme mekanizmasıdır. – Çoğu algoritma kolayca özyinelemeli şekilde çözülebilir. – Fakat sonsuz döngü yapmamaya dikkat edilmeli. 2

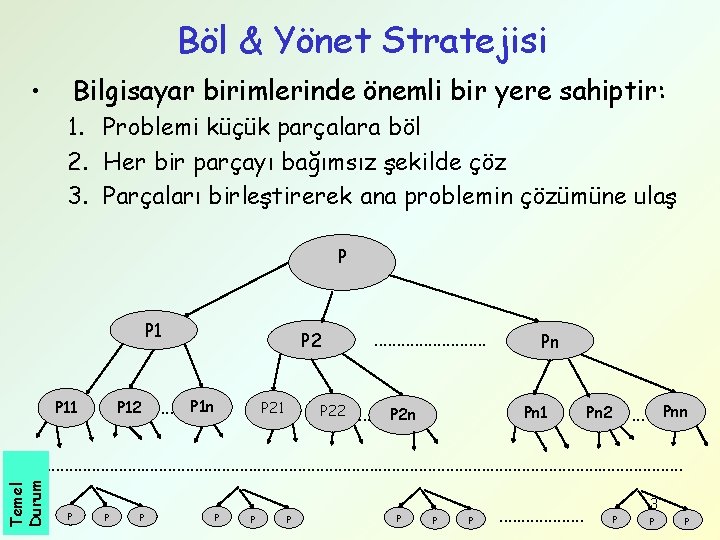
Böl & Yönet Stratejisi • Bilgisayar birimlerinde önemli bir yere sahiptir: 1. Problemi küçük parçalara böl 2. Her bir parçayı bağımsız şekilde çöz 3. Parçaları birleştirerek ana problemin çözümüne ulaş P P 11 P 12 P 2 . . . P 1 n P 21 P 22 . . . Pn Pn 1 . . . P 2 n . . . Pnn Pn 2 Temel Durum . . . . . . . . . P P P P P . . 3 P P P

Böl & Yönet Stratejisi (devam) /* P problemini çöz */ Solve(P){ /* Temel durum(s) */ if P problemi temel durumda ise return çözüm /* (n>=2) için P yi P 1, P 2, . . Pn şeklinde parçalara böl */ /* Problemleri özyinelemeli şekilde çöz */ S 1 = Solve(P 1); /* S 1 için P 1 problemini çöz */ S 2 = Solve(P 2); /* S 2 için P 2 problemini çöz*/ … Sn = Solve(Pn); /* Sn için Pn problemini çöz */ /* Çözüm için parçaları birleştir. */ S = Merge(S 1, S 2, …, Sn); /* Çözümü geri döndür */ return S; } //bitti-Solve 4

N’ye Kadar Olan Sayıların Toplamı • Problemimizin 1’den n’ye kadar sayıların toplamı olduğunu varsayalım. • Bu problemi özyinelemeli nasıl düşüneceğiz: – Topla(n) = 1+2+. . +n ifadesini hesaplamak için • Topla(n-1) = 1+2+. . +n-1 ifadesini hesapla (aynı türden daha küçük bir problem) • Topla(n-1) ifadesine n ekleyerek Topla(n) ifadesi hesaplanır. • Ö. g. , Topla(n) = Topla(n-1) + n; – Temel durumu belirlememiz gerekiyor. • Temel durum, (alt problem) problemi bölmeye gerek kalmadan kolayca çözülebilen problemdir. • n = 1 ise, Topla(1) = 1; 5

N’ye Kadar Olan Sayıların Toplamı /* Topla 1+2+3+…+n */ int Topla(int n){ int ara. Toplam = 0; /* Temel durum */ if (n == 1) return 1; /* Böl ve Yönet */ ara. Toplam = Topla(n-1); Public. . . main(. . . ){ int x = 0; x = Topla(4); print(“x: ”+ x); return 0; } /* bitti-main */ /* Birleştir */ return ara. Toplam + n; } /* bitti-Topla */ 6

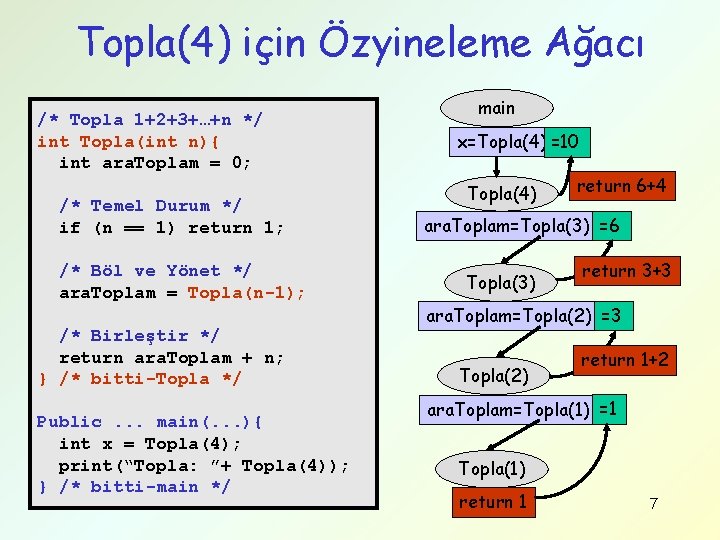
Topla(4) için Özyineleme Ağacı /* Topla 1+2+3+…+n */ int Topla(int n){ int ara. Toplam = 0; /* Temel Durum */ if (n == 1) return 1; /* Böl ve Yönet */ ara. Toplam = Topla(n-1); /* Birleştir */ return ara. Toplam + n; } /* bitti-Topla */ Public. . . main(. . . ){ int x = Topla(4); print(“Topla: ”+ Topla(4)); } /* bitti-main */ main x=Topla(4) =10 Topla(4) return 6+4 ara. Toplam=Topla(3) =6 Topla(3) return 3+3 ara. Toplam=Topla(2) =3 Topla(2) return 1+2 ara. Toplam=Topla(1) =1 Topla(1) return 1 7

Topla(n)’nin çalışma zamanı /* Topla 1+2+3+…+n */ int Topla(int n){ int ara. Toplam = 0; /* Temel durum */ if (n == 1) return 1; /* Böl ve yönet */ ara. Toplam = Topla(n-1); /* Birleştir */ return ara. Toplam + n; } /* bitti-ara. Toplam */ T(n) = n =1 1 (Temel durum) n > 1 T(n-1) + 1

an İfadesini Hesaplama /* a^n hesapla */ double Ust(double a, int n){ double ara. Sonuc; /* Temel durum */ if (n == 0) return 1; else if (n == 1) return a; /* ara. Sonuc = a^(n-1) */ ara. Sonuc = Ust(a, n-1); /* Birleştir */ return ara. Sonuc*a; } /* bitti-Ust */ • Böl yönet & birleştir işlemlerini bir ifade ile yapılabilir. /* Hesapla a^n */ double Ust(double a, int n){ /* Temel durum */ if (n == 0) return 1; else if (n == 1) return a; return Ust(a, n-1)*a; } /* bitti-Ust */ 9

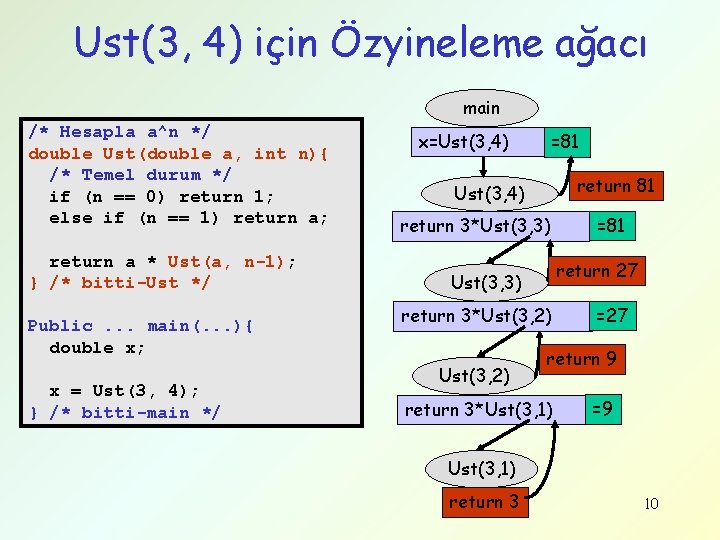
Ust(3, 4) için Özyineleme ağacı main /* Hesapla a^n */ double Ust(double a, int n){ /* Temel durum */ if (n == 0) return 1; else if (n == 1) return a; return a * Ust(a, n-1); } /* bitti-Ust */ Public. . . main(. . . ){ double x; x = Ust(3, 4); } /* bitti-main */ x=Ust(3, 4) =81 return 81 Ust(3, 4) return 3*Ust(3, 3) return 27 Ust(3, 3) return 3*Ust(3, 2) =81 =27 return 9 return 3*Ust(3, 1) =9 Ust(3, 1) return 3 10

Ust(a, n)’nin Çalışma Zamanı /* Hesapla a^n */ double Ust(double a, int n){ /* temel durum */ if (n == 0) return 1; else if (n == 1) return a; return a * Ust(a, n-1); } /* bitti-Ust */ T(n) = n <= 1 1 (Temel durum) N > 1 T(n-1) + 1

Fibonacci Sayıları • Fibonacci sayılarını tanımlayacak olursak: – F(0) = 0 – F(1) = 1 – F(n) = F(n-1) + F(n-2) /* n. Fibonacci sayısını hesaplama*/ int Fibonacci(int n){ /* Temel durum */ if (n == 0) return 0; if (n == 1) return 1; return Fibonacci(n-1) + Fibonacci(n-2); } /* bitti-Fibonacci */ 12

Fibonacci Sayıları (devam) • Fibonacci sayılarının tanımı özyinelemelidir. Dolayısıyla problemi çözmek için özyinelemeli çözmek doğal olarak gözükebilir. • Örneğin 40. fibonacci değerini bulmaya çalışalım. /* n. Fibonacci sayısını hesaplama*/ int Fibonacci(int n){ /* Temel durum */ if (n == 0) return 0; if (n == 1) return 1; return Fibonacci(n-1) + Fibonacci(n-2); } /* bitti-Fibonacci */ 13

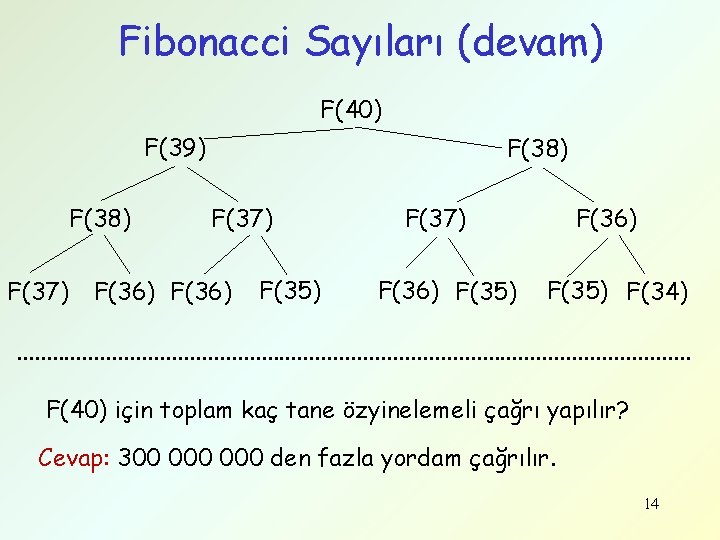
Fibonacci Sayıları (devam) F(40) F(39) F(38) F(37) F(36) F(35) F(34) . . . . . . . F(40) için toplam kaç tane özyinelemeli çağrı yapılır? Cevap: 300 000 den fazla yordam çağrılır. 14

Çözüm - yinelemeli algoritma • Basit bir "for" ile çözülebilecek problemler için özyinelemeli algoritmalar kullanılmaz. • Fibonacci sayıları için yinelemeli algoritmalar kullanılmalı. /* n. Fibonacci sayısını hesaplama*/ public static int fibonacci(int n){ if(n == 1 || n == 2) return 1; int s 1=1, s 2=1, sonuc=0; for(int i=0; i<n; i++){ sonuc = s 1 + s 2; s 1 = s 2; s 2 = sonuc; } return sonuc; } 15

Yapılan Genel Hatalar • Özyinelemeli yordamın temel durumunu unutulmamalı • Basit bir for yerine özyinelemeli yordam kullanmak iyi bir fikir değildir. • Özyinelemeli algoritmanın bitiş şartı temel durumda verilir. Buradaki bir hata özyinelemeli algoritmanın hatalı olmasına neden olur. 16

Uygulama • 17