Zum Starten und Weiterfhren der Prsentation gengt ein

Zum Starten und Weiterführen der Präsentation genügt ein Mausklick! Mit diesen Schaltflächen kann man innerhalb der Präsentation springen! Vorherige Seite Erste Seite Anfang Präsentation beenden Ende Nächste Seite

Intervallschachtelung Hier als Näherungsverfahren zur Bestimmung der Quadratwurzel Anfang Ende

Hinter dem Verfahren steckt die Idee, durch „gezieltes Probieren“ die Quadratwurzel zu finden. Beispiel: Bestimmung der Wurzel aus 10 Zunächst überlegt man sich nur ungefähr, wie groß die Wurzel sein muss. Ich weiß, dass 3² gleich 9 ist. Die 3 ist zu klein! Anfang Hmm, 4²=16, die 4 ist zu groß. Ende

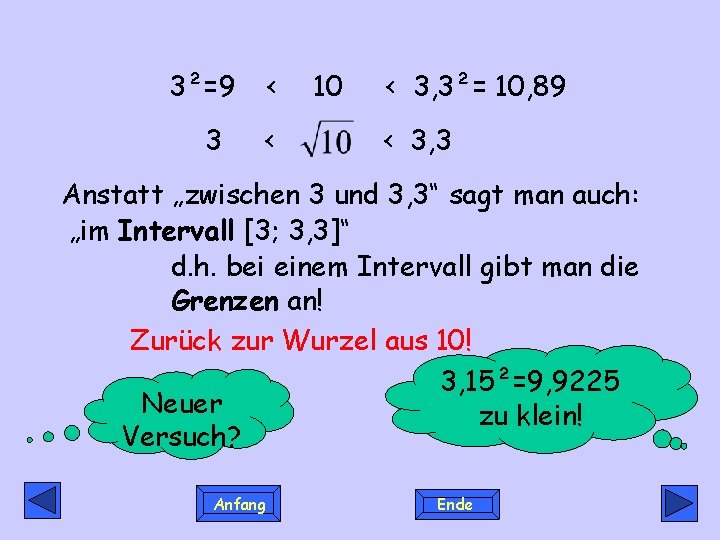
Solche Überlegungen am besten gleich aufschreiben! Die Wurzel aus 10 muss zwischen 3 und 4 liegen: also 3²=9 Nächster Versuch: 3, 3²=10, 89 Ganz gut, aber immer noch zu groß! Anfang 3 < 10 < < 4²= 16 < 4 Die Wurzel muss also zwischen 3 und 3, 3 liegen! Ende

3²=9 3 < < 10 < 3, 3²= 10, 89 < 3, 3 Anstatt „zwischen 3 und 3, 3“ sagt man auch: „im Intervall [3; 3, 3]“ d. h. bei einem Intervall gibt man die Grenzen an! Zurück zur Wurzel aus 10! 3, 15²=9, 9225 Neuer zu klein! Versuch? Anfang Ende

Die Wurzel aus 10 muss zwischen 3, 15 und 3, 3 liegen: „Das heißt, die Wurzel liegt im Intervall [3, 15 ; 3, 3 ]“ 3, 15²=9, 9225 < 3, 15 < 10 < 3, 3²= 10, 89 < 3, 3 So! Bisher sind wir durch Probieren der Wurzel schon ganz schön nahe gekommen. Problem: Wie könnte das ein Computer oder Taschenrechner für uns machen? Anfang Ende

Wir müssen für unser Probierverfahren, eine Art Kochrezept finden – eine immer gleiche Prozedur! Dazu machen wir noch ein zweites Beispiel: Bestimmung der Wurzel aus 2 Vorschlag: Bevor du weiterklickst, versuche doch mal die Wurzel durch das beschriebene Verfahren bis auf 2 Stellen zu bestimmen! Anfang Ende

Kannst du erklären Wir beginnen mit dem Intervall [1; 2] und schauen uns warum? das ganze auf dem Zahlenstrahl an: Falls nein, geh noch mal zurück! Dazwischen muss die Wurzel aus 2 liegen! 1 2 1, 5 = (1+2): 2 Anstatt nun irgendeine Zahl zwischen 1 und 2 zu probieren, nehmen wir die Intervallmitte. 1, 5²= 2, 25 d. h. 1, 5 ist zu groß! Also muss Wurzel aus 2 zwischen 1 und 1, 5 liegen. bzw. im Intervall [1; 1, 5] Anfang Ende

Nun nehmen wir uns das Intervall [1; 1, 5] vor: 1 1, 25 1, 5 2 Wir nehmen die Intervallmitte: (1+1, 5) : 2=1, 25 und überprüfen durch Quadrieren: 1, 25²=1, 5625 Zu klein! Also liegt die Wurzel aus 2 zwischen 1, 25 und 1, 5 bzw. im Intervall [1, 25 ; 1, 5] Anfang Ende

Und nochmal: Intervall [1, 25 ; 1, 5 ] 1 1, 25 1, 375 1, 5 Intervallmitte: Quadrieren: 2 (1, 25+1, 5): 2 = 1, 375²=1, 890625 zu klein! Also liegt zwischen 1, 375 und 1, 5. im Intervall Anfang [1, 375 ; 1, 5] Ende

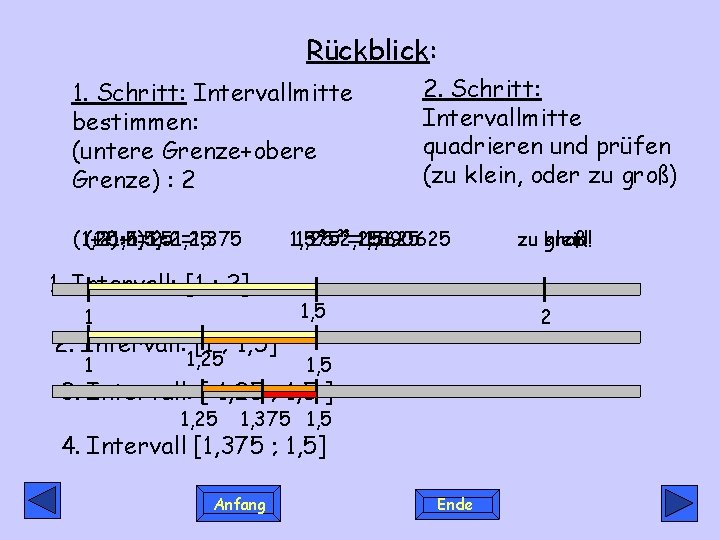
Rückblick: 1. Schritt: Intervallmitte bestimmen: (untere Grenze+obere Grenze) : 2 (1+2): 2=1, 5 (1, 25+1, 5): 2=1, 375 (1+1, 5): 2=1, 25 1. Intervall: [1 ; 2] 1 2. Intervall: [1 ; 1, 5] 1 1, 25 2. Schritt: Intervallmitte quadrieren und prüfen (zu klein, oder zu groß) 1, 5²=2, 25 1, 375²=1, 890625 1, 25²=1, 5625 1, 5 2 1, 5 3. Intervall: [ 1, 25 ; 1, 5 ] 1, 25 1, 375 1, 5 4. Intervall [1, 375 ; 1, 5] Anfang zu klein! groß! Ende

Zur Übersicht wäre doch eine Tabelle gut: untere Grenze obere Grenze Intervallmitte Quadrat IM Prüfergebnis Bevor du weiterklickst, 1 2 1, 5 1, 25 1, 375 1, 5 versuche selbst eine 2, 25 geeignete Tabelle zu erstellen! 1, 5625 Zu groß Zu klein 1, 890625 Zu klein Ehrlich schon selbst probiert? ? Anfang Ende