ZTransform Part 4 Stability Causality System Properties Causality

Z-Transform Part 4 – Stability/ Causality

System Properties: Causality and Stability

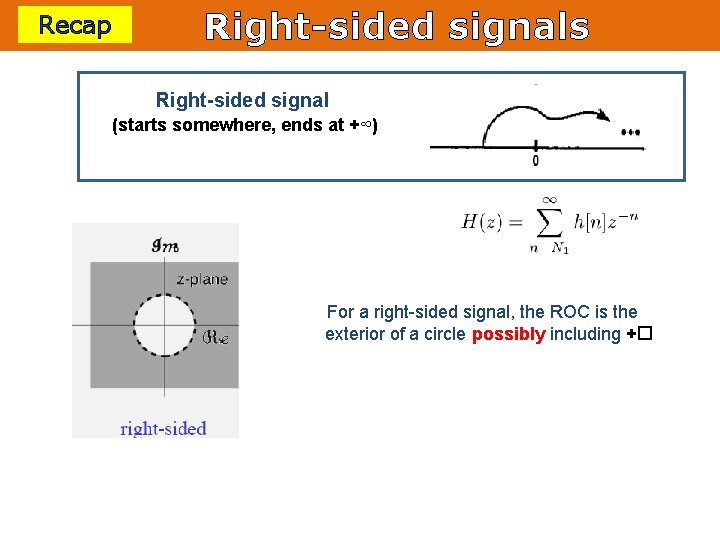
Recap Right-sided signals Right-sided signal (starts somewhere, ends at +∞) For a right-sided signal, the ROC is the exterior of a circle possibly including +�

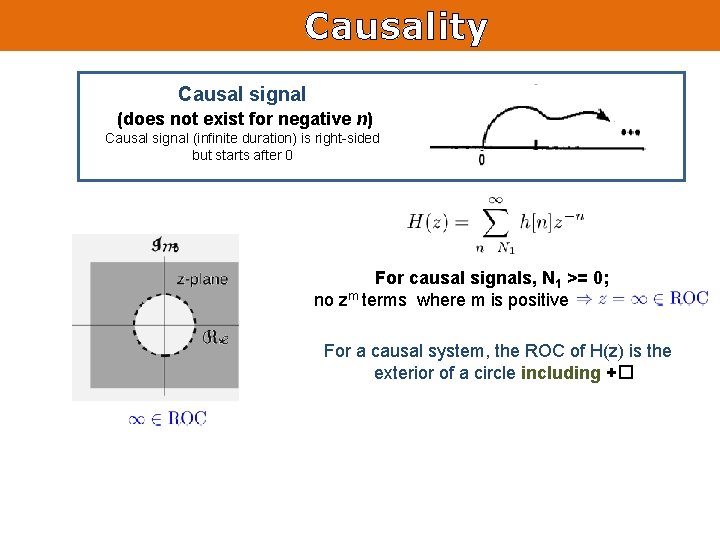
Causality Causal signal (does not exist for negative n) Causal signal (infinite duration) is right-sided but starts after 0 For causal signals, N 1 >= 0; no zm terms where m is positive -------For a causal system, the ROC of H(z) is the exterior of a circle including +�

Causality (from observing H(z)) For a causal system, H(z) does not have poles at z=+� The causality of a signal/ system can be ensured if: 1) The ROC is the exterior of a circle (outside the outermost pole) 2) With H(z) expressed as a ratio of polynomials: the degree of the numerator (M) is no more than the degree of the denominator (N)

Causality: Examples [Oppenheim] Example 10. 20 Causal or not? Example 10. 21 Causal or not?

Stability A LTI system is stable if and only if ROC of its system function H(z) includes the unit circle, |z|=1 When is a system causal and stable? 1) When the ROC is the exterior of a circle (with radius as the magnitude of the outermost pole) 2) The ROC includes � (causality) and unit circle (stability). In other words, for a causal system to be stable, all the poles must be inside the unit circle.

Stability: Examples [Oppenheim] Example 10. 22 Stable or not? Example 10. 22 (contd. ) Stable or not? Causal or not?

References Section 10. 7 [Oppenheim]

? ? ? Questions/ Confusions? For follow-up questions, use: http: //sigandsys. ning. com/